Using the Properties of Triangles to Solve Problems
Learning Outcomes
- Use properties of triangles
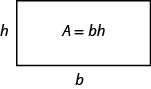 We can divide this rectangle into two congruent triangles (see the image below). Triangles that are congruent have identical side lengths and angles, and so their areas are equal. The area of each triangle is one-half the area of the rectangle, or [latex]\Large\frac{1}{2}\normalsize bh[/latex]. This example helps us see why the formula for the area of a triangle is [latex]A=\Large\frac{1}{2}\normalsize bh[/latex].
A rectangle can be divided into two triangles of equal area. The area of each triangle is one-half the area of the rectangle.
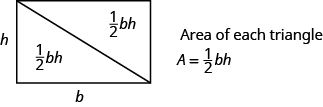
We can divide this rectangle into two congruent triangles (see the image below). Triangles that are congruent have identical side lengths and angles, and so their areas are equal. The area of each triangle is one-half the area of the rectangle, or [latex]\Large\frac{1}{2}\normalsize bh[/latex]. This example helps us see why the formula for the area of a triangle is [latex]A=\Large\frac{1}{2}\normalsize bh[/latex].
A rectangle can be divided into two triangles of equal area. The area of each triangle is one-half the area of the rectangle.
 The formula for the area of a triangle is [latex]A=\Large\frac{1}{2}\normalsize bh[/latex], where [latex]b[/latex] is the base and [latex]h[/latex] is the height.
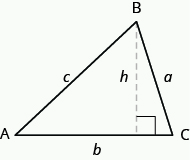
To find the area of the triangle, you need to know its base and height. The base is the length of one side of the triangle, usually the side at the bottom. The height is the length of the line that connects the base to the opposite vertex, and makes a [latex]\text{90}^ \circ[/latex] angle with the base. The image below shows three triangles with the base and height of each marked.
The height [latex]h[/latex] of a triangle is the length of a line segment that connects the the base to the opposite vertex and makes a [latex]\text{90}^ \circ[/latex] angle with the base.
The formula for the area of a triangle is [latex]A=\Large\frac{1}{2}\normalsize bh[/latex], where [latex]b[/latex] is the base and [latex]h[/latex] is the height.
To find the area of the triangle, you need to know its base and height. The base is the length of one side of the triangle, usually the side at the bottom. The height is the length of the line that connects the base to the opposite vertex, and makes a [latex]\text{90}^ \circ[/latex] angle with the base. The image below shows three triangles with the base and height of each marked.
The height [latex]h[/latex] of a triangle is the length of a line segment that connects the the base to the opposite vertex and makes a [latex]\text{90}^ \circ[/latex] angle with the base.

Triangle Properties
For any triangle [latex]\Delta ABC[/latex], the sum of the measures of the angles is [latex]\text{180}^ \circ[/latex].[latex]m\angle{A}+m\angle{B}+m\angle{C}=180^\circ [/latex]
The perimeter of a triangle is the sum of the lengths of the sides.[latex]P=a+b+c[/latex]
The area of a triangle is one-half the base, [latex]b[/latex], times the height, [latex]h[/latex].[latex]A={\Large\frac{1}{2}}bh[/latex]
example
Find the area of a triangle whose base is [latex]11[/latex] inches and whose height is [latex]8[/latex] inches. Solution| Step 1. Read the problem. Draw the figure and label it with the given information. |  |
| Step 2. Identify what you are looking for. | the area of the triangle |
| Step 3. Name. Choose a variable to represent it. | let A = area of the triangle |
| Step 4.Translate. Write the appropriate formula. Substitute. |  |
| Step 5. Solve the equation. | [latex]A=44[/latex] square inches. |
| Step 6. Check: [latex]A={ \Large\frac{1}{2}}bh[/latex] [latex]44\stackrel{?}{=}{ \Large\frac{1}{2}}(11)8[/latex] [latex]44=44\quad\checkmark[/latex] | |
| Step 7. Answer the question. | The area is [latex]44[/latex] square inches. |
try it
[ohm_question]146525[/ohm_question]example
The perimeter of a triangular garden is [latex]24[/latex] feet. The lengths of two sides are [latex]4[/latex] feet and [latex]9[/latex] feet. How long is the third side?Answer: Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. |  |
| Step 2. Identify what you are looking for. | length of the third side of a triangle |
| Step 3. Name. Choose a variable to represent it. | Let c = the third side |
| Step 4.Translate. Write the appropriate formula. Substitute in the given information. |  |
| Step 5. Solve the equation. | [latex]24=13+c[/latex] [latex]11=c[/latex] |
| Step 6. Check: [latex-display]P=a+b+c[/latex-display] [latex-display]24\stackrel{?}{=}4+9+11[/latex-display] [latex]24=24\checkmark[/latex] | |
| Step 7. Answer the question. | The third side is [latex]11[/latex] feet long. |
try it
[ohm_question]146526[/ohm_question]example
The area of a triangular church window is [latex]90[/latex] square meters. The base of the window is [latex]15[/latex] meters. What is the window’s height?Answer: Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. |  |
| Step 2. Identify what you are looking for. | height of a triangle |
| Step 3. Name. Choose a variable to represent it. | Let h = the height |
| Step 4.Translate. Write the appropriate formula. Substitute in the given information. |  |
| Step 5. Solve the equation. | [latex]90={\Large\frac{1}{2}}\normalsize(15)h[/latex] [latex]12=h[/latex] |
| Step 6. Check: [latex-display]A={\Large\frac{1}{2}}\normalsize bh[/latex-display] [latex-display]90\stackrel{?}{=}{\Large\frac{1}{2}}\normalsize\cdot 15\cdot 12[/latex-display] [latex]90=90\quad\checkmark[/latex] | |
| Step 7. Answer the question. | The height of the triangle is [latex]12[/latex] meters. |
try it
[ohm_question]146528[/ohm_question] [ohm_question]146527[/ohm_question]Isosceles and Equilateral Triangles
Besides the right triangle, some other triangles have special names. A triangle with two sides of equal length is called an isosceles triangle. A triangle that has three sides of equal length is called an equilateral triangle. The image below shows both types of triangles. In an isosceles triangle, two sides have the same length, and the third side is the base. In an equilateral triangle, all three sides have the same length.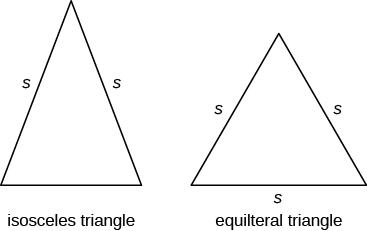
Isosceles and Equilateral Triangles
An isosceles triangle has two sides the same length. An equilateral triangle has three sides of equal length.example
The perimeter of an equilateral triangle is [latex]93[/latex] inches. Find the length of each side.Answer: Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. |  Perimeter = [latex]93[/latex] in.
Perimeter = [latex]93[/latex] in. |
| Step 2. Identify what you are looking for. | length of the sides of an equilateral triangle |
| Step 3. Name. Choose a variable to represent it. | Let s = length of each side |
| Step 4.Translate. Write the appropriate formula. Substitute. |  |
| Step 5. Solve the equation. | [latex]93=3s[/latex] [latex]31=s[/latex] |
Step 6. Check:
 [latex-display]93\stackrel{?}{=}31+31+31[/latex-display]
[latex]93=93\quad\checkmark[/latex]
[latex-display]93\stackrel{?}{=}31+31+31[/latex-display]
[latex]93=93\quad\checkmark[/latex] |
|
| Step 7. Answer the question. | Each side is [latex]31[/latex] inches. |
try it
[ohm_question]146529[/ohm_question]example
Arianna has [latex]156[/latex] inches of beading to use as trim around a scarf. The scarf will be an isosceles triangle with a base of [latex]60[/latex] inches. How long can she make the two equal sides?Answer: Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. |  P = [latex]156[/latex] in.
P = [latex]156[/latex] in. |
| Step 2. Identify what you are looking for. | the lengths of the two equal sides |
| Step 3. Name. Choose a variable to represent it. | Let s = the length of each side |
| Step 4.Translate. Write the appropriate formula. Substitute in the given information. |  |
| Step 5. Solve the equation. | [latex]156=2s=60[/latex] [latex-display]96=2s[/latex-display] [latex]48=s[/latex] |
| Step 6. Check: [latex-display]P=a+b+c[/latex-display] [latex-display]156\stackrel{?}{=}48+60+48[/latex-display] [latex]156=156\quad\checkmark[/latex] | |
| Step 7. Answer the question. | Arianna can make each of the two equal sides [latex]48[/latex] inches long. |
try it
[ohm_question]146531[/ohm_question]Contribute!
Did you have an idea for improving this content? We’d love your input.
Licenses & Attributions
CC licensed content, Original
- Question ID 146531, 146528, 146526, 146525. Authored by: Lumen Learning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex: Find the Area of a Triangle (Whole Number). Authored by: James Sousa (mathispower4u.com). License: CC BY: Attribution.
- Ex: Find the Height of a Triangle Given Area (Even Base). Authored by: James Sousa (mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
