Using the Properties of Circles to Solve Problems
Learning Outcomes
- Find the circumference and area of a circular object given its radius or diameter
- Calculate the diameter or radius of a circular object given its circumference
Properties of Circles
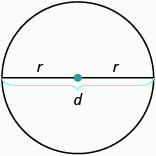
- [latex]r[/latex] is the length of the radius
- [latex]d[/latex] is the length of the diameter
- [latex]d=2r[/latex]
- Circumference is the perimeter of a circle. The formula for circumference is [latex]C=2\pi r[/latex]
- The formula for area of a circle is [latex]A=\pi {r}^{2}[/latex]
example
A circular sandbox has a radius of [latex]2.5[/latex] feet. Find 1. the circumference and 2. the area of the sandbox. Solution| 1. Step 1. Read the problem. Draw the figure and label it with the given information. |  |
| Step 2. Identify what you are looking for. | The circumference of the circle |
| Step 3. Name. Choose a variable to represent it. | Let c = circumference of the circle |
| Step 4. Translate. Write the appropriate formula Substitute | [latex]C=2\pi r[/latex] [latex]C=2\pi \left(2.5\right)[/latex] |
| Step 5. Solve the equation. | [latex]C\approx 2\left(3.14\right)\left(2.5\right)[/latex] [latex]C\approx 15\text{ft}[/latex] |
Step 6. Check. Does this answer make sense?
Yes. If we draw a square around the circle, its sides would be [latex]5[/latex] ft (twice the radius), so its perimeter would be [latex]20[/latex] ft. This is slightly more than the circle's circumference, [latex]15.7[/latex] ft.
 |
|
| Step 7. Answer the question. | The circumference of the sandbox is [latex]15.7[/latex] feet. |
| 2. Step 1. Read the problem. Draw the figure and label it with the given information. |  |
| Step 2. Identify what you are looking for. | The area of the circle |
| Step 3. Name. Choose a variable to represent it. | Let A = the area of the circle |
| Step 4. Translate. Write the appropriate formula Substitute | [latex]A=\pi {r}^{2}[/latex] [latex]A=\pi{\left(2.5\right)}^{2}[/latex] |
| Step 5. Solve the equation. | [latex]A\approx \left(3.14\right){\left(2.5\right)}^{2}[/latex] [latex]A\approx 19.625\text{sq. ft}[/latex] |
| Step 6. Check. Yes. If we draw a square around the circle, its sides would be [latex]5[/latex] ft, as shown in part ⓐ. So the area of the square would be [latex]25[/latex] sq. ft. This is slightly more than the circle's area, [latex]19.625[/latex] sq. ft. | |
| Step 7. Answer the question. | The area of the circle is [latex]19.625[/latex] square feet. |
try it
[ohm_question]146563[/ohm_question] [ohm_question]146564[/ohm_question]example
A circular table has a diameter of four feet. What is the circumference of the table?Answer: Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. |  |
| Step 2. Identify what you are looking for. | The circumference of the table |
| Step 3. Name. Choose a variable to represent it. | Let C = the circumference of the table |
| Step 4. Translate. Write the appropriate formula for the situation. Substitute. | [latex]C=\pi d[/latex] [latex]C=\pi \left(4\right)[/latex] |
| Step 5. Solve the equation, using [latex]3.14[/latex] for [latex]\pi [/latex]. | [latex]C\approx \left(3.14\right)\left(4\right)[/latex] [latex]C\approx 12.56\text{feet}[/latex] |
Step 6. Check: If we put a square around the circle, its side would be [latex]4[/latex].
The perimeter would be [latex]16[/latex]. It makes sense that the circumference of the circle, [latex]12.56[/latex], is a little less than [latex]16[/latex].
 |
|
| Step 7. Answer the question. | The diameter of the table is [latex]12.56[/latex] square feet. |
try it
[ohm_question]146785[/ohm_question] [ohm_question]146786[/ohm_question]example
Find the diameter of a circle with a circumference of [latex]47.1[/latex] centimeters.Answer: Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. |  [latex]C=47.1[/latex]cm
[latex]C=47.1[/latex]cm |
| Step 2. Identify what you are looking for. | The diameter of the circle |
| Step 3. Name. Choose a variable to represent it. | Let [latex]d[/latex] = the diameter of the circle |
| Step 4. Translate. | |
| Write the formula. Substitute, using [latex]3.14[/latex] to approximate [latex]\pi [/latex] . | [latex]C=\pi{d}[/latex] [latex]47.1\approx{3.14d}[/latex] |
| Step 5. Solve. | [latex] \Large\frac{47.1}{3.14}\normalsize\approx \Large\frac{3.14d}{3.14}[/latex] [latex]15\approx{d}[/latex] |
| Step 6. Check: [latex]C=\pi{d}[/latex] [latex-display]47.1\stackrel{?}{=}\left(3.14\right)\left(15\right)[/latex-display] [latex]47.1=47.1\quad\checkmark [/latex] | |
| Step 7. Answer the question. | The diameter of the circle is approximately [latex]15[/latex] centimeters. |
try it
[ohm_question]146787[/ohm_question]Contribute!
Did you have an idea for improving this content? We’d love your input.
Licenses & Attributions
CC licensed content, Original
- Question ID 146787, 146786, 146785. Authored by: Lumen Learning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Examples: Determine the Circumference of a Circle. Authored by: James Sousa (mathispower4u.com). License: CC BY: Attribution.
- Example: Determine the Area of a Circle. Authored by: James Sousa (mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
