The Elimination Method With Multiplication
Learning Outcomes
- Use the elimination method with multiplication
- Express the solution of a dependent system of equations containing two variables
Solve a system of equations when multiplication is necessary to eliminate a variable
Many times adding the equations or adding the opposite of one of the equations will not result in eliminating a variable. Look at the system below. [latex-display]\begin{array}{r}3x+4y=52\\5x+y=30\end{array}[/latex-display] If you add the equations above, or add the opposite of one of the equations, you will get an equation that still has two variables. So let’s now use the multiplication property of equality first. You can multiply both sides of one of the equations by a number that will allow you to eliminate the same variable in the other equation. We do this with multiplication. Notice that the first equation contains the term [latex]4y[/latex], and the second equation contains the term [latex]y[/latex]. If you multiply the second equation by [latex]−4[/latex], when you add both equations the y variables will add up to [latex]0[/latex]. The following example takes you through all the steps to find a solution to this system.Example
Solve for [latex]x[/latex] and [latex]y[/latex]. Equation A: [latex]3x+4y=52[/latex] Equation B: [latex]5x+y=30[/latex]Answer: Look for terms that can be eliminated. The equations do not have any x or y terms with the same coefficients. [latex-display]\begin{array}{r}3x+4y=52\\5x+y=30\end{array}[/latex-display] Multiply the second equation by [latex]−4[/latex] so they do have the same coefficient. [latex-display]\begin{array}{l}\,\,\,\,\,\,\,\,\,3x+4y=52\\−4\left(5x+y\right)=−4\left(30\right)\end{array}[/latex-display] Rewrite the system and add the equations. [latex-display]\begin{array}{r}3x+4y=52\,\,\,\,\,\,\,\\−20x–4y=−120\end{array}[/latex-display] Solve for [latex]x[/latex]. [latex-display]\begin{array}{l}−17x=-68\\\,\,\,\,\,\,\,\,\,\,x=4\end{array}[/latex-display] Substitute [latex]x=4[/latex] into one of the original equations to find y. [latex-display]\begin{array}{r}3x+4y=52\\3\left(4\right)+4y=52\\12+4y=52\\4y=40\\y=10\end{array}[/latex-display] Check your answer. [latex-display]\begin{array}{r}3x+4y=52\\3\left(4\right)+4\left(10\right)=52\\12+40=52\\52=52\\\text{TRUE}\\\\5x+y=30\\5\left(4\right)+10=30\\20+10=30\\30=30\\\text{TRUE}\end{array}[/latex-display] The answers check.
Answer
The solution is [latex](4, 10)[/latex].Example
Solve the given system of equations by the elimination method.[latex]\begin{array}{l}3x+5y=-11\hfill \\ x - 2y=11\hfill \end{array}[/latex]
Answer: Adding these equations as presented will not eliminate a variable. However, we see that the first equation has [latex]3x[/latex] in it and the second equation has [latex]x[/latex]. So if we multiply the second equation by [latex]-3,\text{}[/latex] the x-terms will add to zero.
[latex]\begin{array}\ \hfill 3x+5y=−11 \\ \hfill −3x+6y=−33 \\ \text{_____________} \\ \hfill 11y=−44 \\ \hfill y=−4 \end{array}[/latex]
For the last step, we substitute [latex]y=-4[/latex] into one of the original equations and solve for [latex]x[/latex].[latex]\begin{array}{c}3x+5y=-11\\ 3x+5\left(-4\right)=-11\\ 3x - 20=-11\\ 3x=9\\ x=3\end{array}[/latex]
Our solution is the ordered pair [latex]\left(3,-4\right)[/latex]. Check the solution in the original second equation.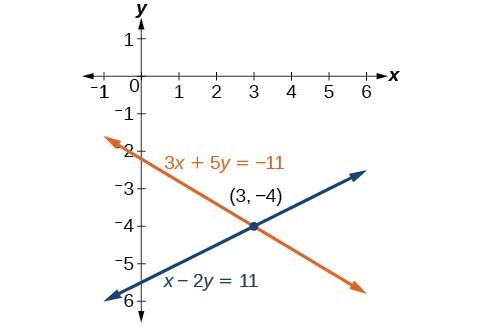
Example
Solve for [latex]x[/latex] and [latex]y[/latex]. [latex-display]\begin{array}{r}3x+4y=52\\5x+y=30\end{array}[/latex-display]Answer: Look for terms that can be eliminated. The equations do not have any x or y terms with the same coefficient. [latex-display]\begin{array}{r}3x+4y=52\\5x+y=30\end{array}[/latex-display] In order to use the elimination method, you have to create variables that have the same coefficient—then you can eliminate them. Multiply the top equation by [latex]5[/latex]. [latex-display]\begin{array}{r}5\left(3x+4y\right)=5\left(52\right)\\5x+y =30\,\,\,\,\,\,\,\,\,\,\,\,\\15x+20y=260\,\,\,\,\,\,\\5x+y=30\,\,\,\,\,\,\,\,\,\end{array}[/latex-display] Now multiply the bottom equation by [latex]−3[/latex]. [latex-display]\begin{array}{r}15x+20y=260\,\,\,\,\,\,\,\,\\-3(5x+y)=−3(30)\\15x+20y=260\,\,\,\,\,\,\,\,\\−15x–3y=−90\,\,\,\,\,\,\,\end{array}[/latex-display] Next add the equations, and solve for [latex]y[/latex]. [latex-display]\begin{array}{r}15x+20y=260\\−15x–3y=\,–90\\17y=170\\y=\,\,\,10\end{array}[/latex-display] Substitute [latex]y=10[/latex] into one of the original equations to find [latex]x[/latex]. [latex-display]\begin{array}{r}3x+4y=52\\3x+4\left(10\right)=52\\3x+40=52\\3x=12\\x=4\,\,\,\end{array}[/latex-display] You arrive at the same solution as before.
Answer
The solution is [latex](4, 10)[/latex].Example
Solve the given system of equations in two variables by elimination.Answer: One equation has [latex]2x[/latex] and the other has [latex]5x[/latex]. The least common multiple is [latex]10x[/latex], so we will have to multiply both equations by a constant in order to eliminate one variable. Let’s eliminate [latex]x[/latex] by multiplying the first equation by [latex]-5[/latex] and the second equation by [latex]2[/latex].
[latex]\begin{array}\ −10x−15y=80 \\ \:\:10x−20y=60 \\ \text{______________} \\ \text{ }\:\:\:\:\:\:\:\:\:\:−35y=140 \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:y=−4 \end{array}[/latex]
Substitute [latex]y=-4[/latex] into the original first equation.[latex]\begin{array}{c}2x+3\left(-4\right)=-16\\ 2x - 12=-16\\ 2x=-4\\ x=-2\end{array}[/latex]
The solution is [latex]\left(-2,-4\right)[/latex]. Check it in the second original equation.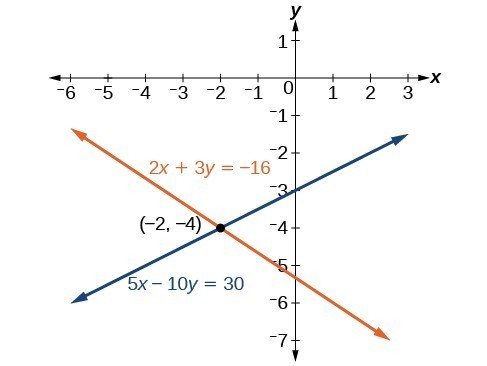
How To: Given a system of equations, solve using the elimination method
- Write both equations with x and y-variables on the left side of the equal sign and constants on the right.
- Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable.
- Substitute that value into one of the original equations and solve for the second variable.
- Check the solution by substituting the values into the other equation.
Try It
[ohm_question]38343[/ohm_question]Example
Solve the given system of equations in two variables by elimination.[latex]\begin{array}{l}\dfrac{x}{3}+\dfrac{y}{6}=3\hfill \\ \dfrac{x}{2}-\dfrac{y}{4}=\text{ }1\hfill \end{array}[/latex]
Answer: First clear each equation of fractions by multiplying both sides of the equation by the least common denominator
[latex]\begin{array}{l}6\left(\dfrac{x}{3}+\dfrac{y}{6}\right)=6\left(3\right)\hfill \\ \text{ }2x+y=18\hfill \\ 4\left(\dfrac{x}{2}-\dfrac{y}{4}\right)=4\left(1\right)\hfill \\ \text{ }2x-y=4\hfill \end{array}[/latex]
Now multiply the second equation by [latex]-1[/latex] so that we can eliminate the x-variable.[latex]\begin{array}{l}-1\left(2x-y\right)=-1\left(4\right)\hfill \\ \text{ }-2x+y=-4\hfill \end{array}[/latex]
Add the two equations to eliminate the x-variable and solve the resulting equation.[latex]\begin{array}\ \hfill 2x+y=18 \\ \hfill−2x+y=−4 \\ \text{_____________} \\ \hfill 2y=14 \\ \hfill y=7 \end{array}[/latex]
Substitute [latex]y=7[/latex] into the first equation.[latex]\begin{array}{l}2x+\left(7\right)=18\hfill \\ \text{ }2x=11\hfill \\ \text{ }x=\dfrac{11}{2}\hfill \end{array}[/latex]
The solution is [latex]\left(\dfrac{11}{2},7\right)[/latex]. Check it in the other equation.[latex]\begin{array}{c}2x-y=4\\ 2(\dfrac{11}{2})-7=4\\ 11-7=4 \\ 4=4\end{array}[/latex]
Example
Find a solution to the system of equations using the elimination method.[latex]\begin{array}{c}x+3y=2\\ 3x+9y=6\end{array}[/latex]
Answer: With the elimination method, we want to eliminate one of the variables by adding the equations. In this case, focus on eliminating [latex]x[/latex]. If we multiply both sides of the first equation by [latex]-3[/latex], then we will be able to eliminate the [latex]x[/latex] -variable.
[latex]\begin{array}{l}\text{ }x+3y=2\hfill \\ \left(-3\right)\left(x+3y\right)=\left(-3\right)\left(2\right)\hfill \\ \text{ }-3x - 9y=-6\hfill \end{array}[/latex]
Now add the equations.[latex]\begin{array} \hfill−3x−9y=−6 \\ \hfill3x+9y=6 \\ \hfill \text{_____________} \\ \hfill 0=0 \end{array}[/latex]
We can see that there will be an infinite number of solutions that satisfy both equations. If we rewrote both equations in slope-intercept form, we might know what the solution would look like before adding. Look at what happens when we convert the system to slope-intercept form.[latex]\begin{array}{l}\text{ }x+3y=2\hfill \\ \text{ }3y=-x+2\hfill \\ \text{ }y=-\dfrac{1}{3}x+\dfrac{2}{3}\hfill \\ 3x+9y=6\hfill \\ \text{ }9y=-3x+6\hfill \\ \text{ }y=-\dfrac{3}{9}x+\dfrac{6}{9}\hfill \\ \text{ }y=-\dfrac{1}{3}x+\dfrac{2}{3}\hfill \end{array}[/latex]
See the graph below. Notice the results are the same. The general solution to the system is [latex]\left(x, -\dfrac{1}{3}x+\dfrac{2}{3}\right)[/latex].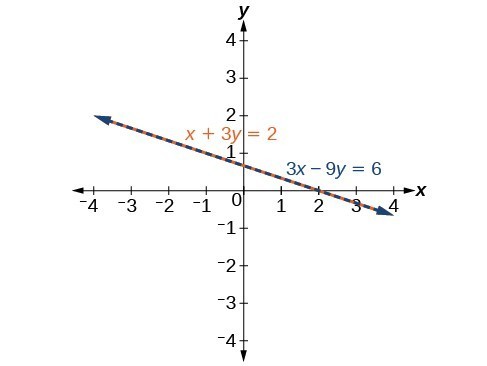
Try It
[ohm_question]115192[/ohm_question]Summary
Multiplication can be used to set up matching terms in equations before they are combined to aid in finding a solution to a system. When using the multiplication method, it is important to multiply all the terms on both sides of the equation—not just the one term you are trying to eliminate.
Contribute!
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex: System of Equations Using Elimination (Infinite Solutions). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
- Ex 2: Solve a System of Equations Using the Elimination Method. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
