We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > ALGEBRA / TRIG I

Evaluating Exponential Expressions

Learning Outcomes

  • Evaluate exponential expressions
Image of a woman taking a picture with a camera repeated five times in different colors. Repeated Image

Anatomy of exponential terms

We use exponential notation to write repeated multiplication of the same quantity. For example, [latex]{2}^{4}[/latex] means to multiply four factors of [latex]2[/latex], so [latex]{2}^{4}[/latex] means [latex]2\cdot 2\cdot 2\cdot 2[/latex].  Conversely, [latex]10\cdot10\cdot10[/latex] can be written more succinctly as [latex]10^{3}[/latex]. The [latex]10[/latex] in [latex]10^{3}[/latex] is called the base. The [latex]3[/latex] in [latex]10^{3}[/latex] is called the exponent. The expression [latex]10^{3}[/latex] is called the exponential expression. Knowing the names for the parts of an exponential expression or term will help you learn how to perform mathematical operations on them.

Exponential Notation

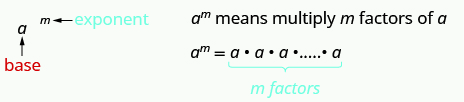On the left side, a raised to the m is shown. The m is labeled in blue as an exponent. The a is labeled in red as the base. On the right, it says a to the m means multiply m factors of a. Below this, it says a to the m equals a times a times a times a, with m factors written below in blue. This is read [latex]a[/latex] to the [latex]{m}^{\mathrm{th}}[/latex] power.
In the expression [latex]{a}^{m}[/latex], the exponent tells us how many times we use the base [latex]a[/latex] as a factor. On the left side, 7 to the 3rd power is shown. Below is 7 times 7 times 7, with 3 factors written below. On the right side, parentheses negative 8 to the 5th power is shown. Below is negative 8 times negative 8 times negative 8 times negative 8 times negative 8, with 5 factors written below. [latex]10^{3}[/latex] is read as “[latex]10[/latex] to the third power” or “[latex]10[/latex] cubed.” It means [latex]10\cdot10\cdot10[/latex], or [latex]1,000[/latex]. [latex]8^{2}[/latex] is read as “[latex]8[/latex] to the second power” or “[latex]8[/latex] squared.” It means [latex]8\cdot8[/latex], or [latex]64[/latex]. [latex]5^{4}[/latex] is read as “[latex]5[/latex] to the fourth power.” It means [latex]5\cdot5\cdot5\cdot5[/latex], or [latex]625[/latex]. [latex]b^{5}[/latex] is read as “b to the fifth power.” It means [latex]{b}\cdot{b}\cdot{b}\cdot{b}\cdot{b}[/latex]. Its value will depend on the value of b. The exponent applies only to the number that it is next to. Therefore, in the expression [latex]xy^{4}[/latex], only the [latex]y[/latex] is affected by the [latex]4[/latex]. [latex]xy^{4}[/latex] means [latex]{x}\cdot{y}\cdot{y}\cdot{y}\cdot{y}[/latex]. If the exponential expression is negative, such as [latex]−3^{4}[/latex], it means [latex]–\left(3\cdot3\cdot3\cdot3\right)[/latex] or [latex]−81[/latex]. If [latex]−3[/latex] is to be the base, it must be written as [latex]\left(−3\right)^{4}[/latex], which means [latex]−3\cdot−3\cdot−3\cdot−3[/latex], or [latex]81[/latex]. Likewise, [latex]\left(−x\right)^{4}=\left(−x\right)\cdot\left(−x\right)\cdot\left(−x\right)\cdot\left(−x\right)=x^{4}[/latex], while [latex]−x^{4}=–\left(x\cdot x\cdot x\cdot x\right)[/latex]. You can see that there is quite a difference, so you have to be very careful! The following examples show how to identify the base and the exponent, as well as how to identify the expanded and exponential format of writing repeated multiplication.  

Example

Identify the exponent and the base in the following terms, then simplify:
  1. [latex]7^{2}[/latex]
  2. [latex]{\left(\frac{1}{2}\right)}^{3}[/latex]
  3. [latex]2x^{3}[/latex]
  4. [latex]\left(-5\right)^{2}[/latex]

Answer:

1) [latex]7^{2}[/latex] The exponent in this term is [latex]2[/latex] and the base is [latex]7[/latex]. To simplify, expand the term: [latex]7^{2}=7\cdot{7}=49[/latex] 2) [latex]{\left(\frac{1}{2}\right)}^{3}[/latex] The exponent on this term is [latex]3[/latex], and the base is [latex]\frac{1}{2}[/latex]. To simplify, expand the multiplication and remember how to multiply fractions: [latex]{\left(\frac{1}{2}\right)}^{3}=\frac{1}{2}\cdot{\frac{1}{2}}\cdot{\frac{1}{2}}=\frac{1}{8}[/latex] 3)  [latex]2x^{3}[/latex] The exponent on this term is [latex]3[/latex], and the base is [latex]x[/latex], the [latex]2[/latex] is not getting the exponent because there are no parentheses that tell us it is.  This term is in its most simplified form. 4) [latex]\left(-5\right)^{2}[/latex] The exponent on this terms is [latex]2[/latex] and the base is [latex]-5[/latex]. To simplify, expand the multiplication: [latex]\left(-5\right)^{2}=-5\cdot{-5}=25[/latex]  

In the following video you are provided more examples of applying exponents to various bases.

https://youtu.be/ocedY91LHKU Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.

example

Simplify: 1. [latex]{5}^{3}[/latex] 2. [latex]{9}^{1}[/latex] Solution
1.
[latex]{5}^{3}[/latex]
Multiply [latex]3[/latex] factors of [latex]5[/latex]. [latex]5\cdot 5\cdot 5[/latex]
Simplify. [latex]125[/latex]
2.
[latex]{9}^{1}[/latex]
Multiply [latex]1[/latex] factor of [latex]9[/latex]. [latex]9[/latex]
 

try it

[ohm_question]146094[/ohm_question]
 

example

Simplify: 1. [latex]{\left({\Large\frac{7}{8}}\right)}^{2}[/latex] 2. [latex]{\left(0.74\right)}^{2}[/latex]

Answer: Solution

1.
[latex]{\left({\Large\frac{7}{8}}\right)}^{2}[/latex]
Multiply two factors. [latex]\left({\Large\frac{7}{8}}\right)\left({\Large\frac{7}{8}}\right)[/latex]
Simplify. [latex]{\Large\frac{49}{64}}[/latex]
2.
[latex]{\left(0.74\right)}^{2}[/latex]
Multiply two factors. [latex]\left(0.74\right)\left(0.74\right)[/latex]
Simplify. [latex]0.5476[/latex]

 

try it

[ohm_question]146095[/ohm_question] [ohm_question]146867[/ohm_question]
 

example

Simplify: 1. [latex]{\left(-3\right)}^{4}[/latex] 2. [latex]{-3}^{4}[/latex]

Answer: Solution

1.
[latex]{\left(-3\right)}^{4}[/latex]
Multiply four factors of [latex]−3[/latex]. [latex]\left(-3\right)\left(-3\right)\left(-3\right)\left(-3\right)[/latex]
Simplify. [latex]81[/latex]
2.
[latex]{-3}^{4}[/latex]
Multiply two factors. [latex]-\left(3\cdot 3\cdot 3\cdot 3\right)[/latex]
Simplify. [latex]-81[/latex]
Notice the similarities and differences in parts 1 and 2. Why are the answers different? In part 1 the parentheses tell us to raise the [latex](−3)[/latex] to the [latex]4[/latex]th power. In part 2 we raise only the [latex]3[/latex] to the [latex]4[/latex]th power and then find the opposite.

 

try it

[ohm_question]146097[/ohm_question]

Evaluate expressions

Evaluating expressions containing exponents is the same as evaluating the linear expressions from earlier in the course. You substitute the value of the variable into the expression and simplify. You can use the order of operations to evaluate the expressions containing exponents. First, evaluate anything in Parentheses or grouping symbols. Next, look for Exponents, followed by Multiplication and Division (reading from left to right), and lastly, Addition and Subtraction (again, reading from left to right). So, when you evaluate the expression [latex]5x^{3}[/latex] if [latex]x=4[/latex], first substitute the value [latex]4[/latex] for the variable [latex]x[/latex]. Then evaluate, using order of operations.

Example

Evaluate [latex]5x^{3}[/latex] if [latex]x=4[/latex].

Answer: Substitute [latex]4[/latex] for the variable [latex]x[/latex].

[latex]5\cdot4^{3}[/latex]

Evaluate [latex]4^{3}[/latex]. Multiply.

[latex]5\left(4\cdot4\cdot4\right)=5\cdot64=320[/latex]

Answer

[latex-display]5x^{3}=320[/latex] when [latex]x=4[/latex-display]

In the example below, notice how adding parentheses can change the outcome when you are simplifying terms with exponents.

Example

Evaluate [latex]\left(5x\right)^{3}[/latex] if [latex]x=4[/latex].

Answer: Substitute [latex]4[/latex] for the variable [latex]x[/latex].

[latex]\left(5\cdot4\right)3[/latex]

Multiply inside the parentheses, then apply the exponent—following the rules of PEMDAS.

[latex]20^{3}[/latex]

Evaluate [latex]20^{3}[/latex].

[latex]20\cdot20\cdot20=8,000[/latex]

Answer

[latex-display]\left(5x\right)3=8,000[/latex] when [latex]x=4[/latex-display]

The addition of parentheses made quite a difference! Parentheses allow you to apply an exponent to variables or numbers that are multiplied, divided, added, or subtracted to each other.

Try It

[ohm_question]53024[/ohm_question]

Example

Evaluate [latex]x^{3}[/latex] if [latex]x=−4[/latex].

Answer: Substitute [latex]−4[/latex] for the variable x.

[latex]\left(−4\right)^{3}[/latex]

Evaluate. Note how placing parentheses around the [latex]−4[/latex] means the negative sign also gets multiplied.

[latex]−4\cdot−4\cdot−4[/latex]

Multiply.

[latex]−4\cdot−4\cdot−4=−64[/latex]

Answer

[latex-display]x^{3}=−64[/latex] when [latex]x=−4[/latex-display]

Caution Caution! Whether to include a negative sign as part of a base or not often leads to confusion. To clarify whether a negative sign is applied before or after the exponent, here is an example.   What is the difference in the way you would evaluate these two terms?
  1. [latex]-{3}^{2}[/latex]
  2. [latex]{\left(-3\right)}^{2}[/latex]
To evaluate 1), you would apply the exponent to the three first, then apply the negative sign last, like this:

[latex]\begin{array}{c}-\left({3}^{2}\right)\\=-\left(9\right) = -9\end{array}[/latex]

To evaluate 2), you would apply the exponent to the [latex]3[/latex] and the negative sign:

[latex]\begin{array}{c}{\left(-3\right)}^{2}\\=\left(-3\right)\cdot\left(-3\right)\\={ 9}\end{array}[/latex]

The key to remembering this is to follow the order of operations. The first expression does not include parentheses so you would apply the exponent to the integer [latex]3[/latex] first, then apply the negative sign. The second expression includes parentheses, so hopefully you will remember that the negative sign also gets squared.

In the next sections, you will learn how to simplify expressions that contain exponents. Come back to this page if you forget how to apply the order of operations to a term with exponents, or forget which is the base and which is the exponent!

In the following video you are provided with examples of evaluating exponential expressions for a given number.

https://youtu.be/pQNz8IpVVg0

Contribute!

Did you have an idea for improving this content? We’d love your input.

Licenses & Attributions

CC licensed content, Original

  • Simplify Basic Exponential Expressions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
  • Screenshot: Repeated Image. Provided by: Lumen Learning License: CC BY: Attribution.
  • Evaluate Basic Exponential Expressions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.

CC licensed content, Shared previously

  • Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.