Graphing Quadratic Functions
Learning Outcomes
- Graph quadratic functions using tables and transformations
- Identify important features of the graphs of quadratic functions
Graphing Quadratic Functions Using Tables
Graph [latex]f(x)=x^{2}[/latex]. Start with a table of values. Then think of each row of the table as an ordered pair.| x | f(x) |
|---|---|
| [latex]−2[/latex] | [latex]4[/latex] |
| [latex]−1[/latex] | [latex]1[/latex] |
| [latex]0[/latex] | [latex]0[/latex] |
| [latex]1[/latex] | [latex]1[/latex] |
| [latex]2[/latex] | [latex]4[/latex] |
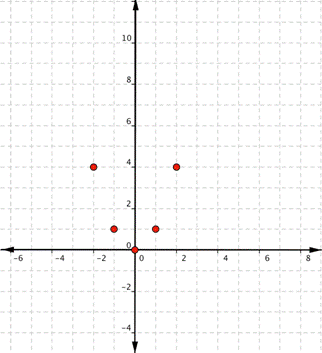Since the points are not on a line, you cannot use a straight edge. Connect the points as best as you can using a smooth curve (not a series of straight lines). You may want to find and plot additional points (such as the ones in blue here). Placing arrows on the tips of the lines implies that they continue in that direction forever.
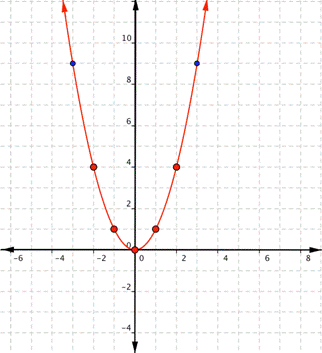The equations for quadratic functions have the form [latex]f(x)=ax^{2}+bx+c[/latex] where [latex] a\ne 0[/latex]. In the basic graph above, [latex]a=1[/latex], [latex]b=0[/latex], and [latex]c=0[/latex].
In the following video, we show an example of plotting a quadratic function using a table of values.
https://youtu.be/wYfEzOJugS8
Graphing Quadratic Functions Using Transformations
Notice that the shape of [latex]f(x)=x^2[/latex] is similar to the letter U. This is called a parabola. One-half of the parabola is a mirror image of the other half. The lowest point on this graph is called the vertex. The vertical line that goes through the vertex is called the line of reflection. In the case of [latex]f(x)=x^2[/latex], that line is the y-axis. All quadratic functions have graphs in the shape of a parabola. However, the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] change the direction, shape, and position of the graph. below, we will discuss how changing these values can transform a graph.How [latex]a[/latex] affects the graph of [latex]f(x)=ax^{2}+bx+c[/latex]
The value of [latex]a[/latex] tells us whether the parabola opens upwards ([latex]a>0[/latex]) or downwards ([latex]a<0[/latex]). If [latex]a[/latex] is positive, the vertex is the lowest point on the graph and the graph opens upward. If a is negative, the vertex is the highest point on the graph and the graph opens downward. The value of [latex]a[/latex] also tells us about the width the graph. When [latex]|a|>1[/latex] the graph will appear more narrow than [latex]f(x)=x^2[/latex]. When [latex]|a|<1[/latex] the graph will appear wider than [latex]f(x)=x^2[/latex]. In the following example, we show how changing the value of [latex]a[/latex] will affect the graph of the function.Example
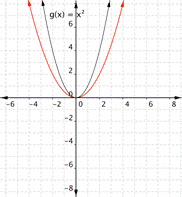
Match each function with its graph. a) [latex] \displaystyle f(x)=3{{x}^{2}}[/latex] b) [latex] \displaystyle f(x)=-3{{x}^{2}}[/latex] c) [latex] \displaystyle f(x)=\frac{1}{2}{{x}^{2}}[/latex] 1)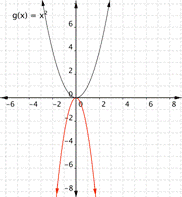
2)
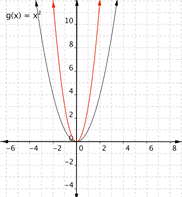3)
Answer:
Function a) matches graph [latex]2[/latex]
Function b) matches graph [latex]1[/latex]
Function c) matches graph [latex]3[/latex]
Function a) [latex] \displaystyle f(x)=3{{x}^{2}}[/latex] means that inputs are squared and then multiplied by three, so the outputs will be greater than they would have been for [latex]f(x)=x^2[/latex]. This results in a parabola that has been squeezed, so graph [latex]2[/latex] is the best match for this function.
Function b) [latex] \displaystyle f(x)=-3{{x}^{2}}[/latex] means that inputs are squared and then multiplied by negative three, so the outputs will be farther away from the [latex]x[/latex]-axis than they would have been for [latex]f(x)=x^2[/latex], but negative in value, so graph [latex]1[/latex] is the best match for this function.
Function c) [latex] \displaystyle f(x)=\frac{1}{2}{{x}^{2}}[/latex] means that inputs are squared then multiplied by [latex]\dfrac{1}{2}[/latex], so the outputs are less than they would be for [latex]f(x)=x^2[/latex]. This results in a parabola that has been opened wider than[latex]f(x)=x^2[/latex]. Graph [latex]3[/latex] is the best match for this function.
How [latex]b[/latex] affects graphs of quadratic functions
When a quadratic function is in the form [latex]f(x)=ax^2+c[/latex], meaning there is no b term, changing c moves the parabola up or down along the y-axis. In the next example, we show how changes to c affect the graph of the function.Example
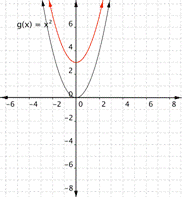
Match each of the following functions with its graph. a) [latex] \displaystyle f(x)={{x}^{2}}+3[/latex] b) [latex] \displaystyle f(x)={{x}^{2}}-3[/latex] 1)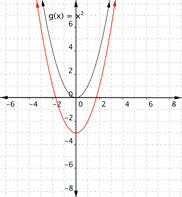
2)
Answer:
Function a) [latex] \displaystyle f(x)={{x}^{2}}+3[/latex] means square the inputs then add three, so every output will be moved up [latex]3[/latex] units. The graph that matches this function best is [latex]2[/latex].
Function b) [latex] \displaystyle f(x)={{x}^{2}}-3[/latex] means square the inputs then subtract three, so every output will be moved down [latex]3[/latex] units. The graph that matches this function best is [latex]1[/latex].
[latex]f(0)=a(0)^2+b(0)+c=c[/latex]
For a quadratic equation, the y-intercept is the point [latex](0,c)[/latex].Finding the Vertex of a Parabola
Changing [latex]b[/latex] moves the line of reflection, which is the vertical line that passes through the vertex (the high or low point) of the parabola. It may help to know how to calculate the vertex of a parabola to understand how changing the value of [latex]b[/latex] in a function will change its graph. To find the vertex of the parabola, use the formula [latex] \displaystyle \left( \frac{-b}{2a},f\left( \frac{-b}{2a} \right) \right)[/latex]. For example, if the function being considered is [latex]f(x)=2x^2-3x+4[/latex], to find the vertex, first calculate [latex]\dfrac{-b}{2a}[/latex] [latex]a = 2[/latex], and [latex]b = -3[/latex], therefore [latex]\dfrac{-b}{2a}=\dfrac{-(-3)}{2(2)}=\dfrac{3}{4}[/latex]. This is the [latex]x[/latex] value of the vertex. Now evaluate the function at [latex]x =\dfrac{3}{4}[/latex] to get the corresponding y-value for the vertex. [latex]f\left( \dfrac{-b}{2a} \right)=2\left(\dfrac{3}{4}\right)^2-3\left(\dfrac{3}{4}\right)+4=2\left(\dfrac{9}{16}\right)-\dfrac{9}{4}+4=\dfrac{18}{16}-\dfrac{9}{4}+4=\dfrac{9}{8}-\dfrac{9}{4}+4=\dfrac{9}{8}-\dfrac{18}{8}+\dfrac{32}{8}=\dfrac{23}{8}[/latex]. The vertex is at the point [latex]\left(\dfrac{3}{4},\dfrac{23}{8}\right)[/latex]. This means that the vertical line of reflection passes through this point as well. It is not easy to tell how changing the values for [latex]b[/latex] will change the graph of a quadratic function, but if you find the vertex, you can tell how the graph will change. In the next example, we show how changing b can change the graph of the quadratic function.Example
Match each of the following functions with its graph. a) [latex] \displaystyle f(x)={{x}^{2}}+2x[/latex] b) [latex] \displaystyle f(x)={{x}^{2}}-2x[/latex] a)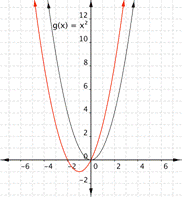
b)
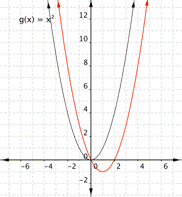
Answer:
Find the vertex of function a)
[latex] \displaystyle f(x)={{x}^{2}}+2x[/latex].
[latex-display]a = 1, b = 2[/latex-display]
x-value:
[latex-display]\dfrac{-b}{2a}=\dfrac{-2}{2(1)}=-1[/latex-display]
y-value:
[latex]f(\dfrac{-b}{2a})=(-1)^2+2(-1)=1-2=-1[/latex].
Vertex = [latex](-1,-1)[/latex], which means the graph that best fits this function is a)
Find the vertex of function b)
[latex]f(x)={{x}^{2}}-2x[/latex].
[latex-display]a = 1, b = -2[/latex-display]
x-value:
[latex-display]\dfrac{-b}{2a}=\dfrac{2}{2(1)}=1[/latex-display]
y-value:
[latex]f(\dfrac{-b}{2a})=(1)^2-2(1)=1-2=-1[/latex].
Vertex = [latex](1,-1)[/latex], which means the graph that best fits this function is b)
Features of a Parabola
We have learned some important things about the graphs of quadratic functions that will make it easier for us to create a graph of a quadratic function. These features of a parabola are summarized in the textbox below:Important Features of the Graphs of Quadratic Functions
For [latex] \displaystyle f(x)=a{{x}^{2}}+bx+c[/latex], where a, b, and c are real numbers,- The parabola opens upward if [latex]a > 0[/latex] and downward if [latex]a < 0[/latex].
- a changes the width of the parabola. The parabola gets narrower if [latex]|a|> 1[/latex] and wider if [latex]|a|<1[/latex].
- The y-intercept of the parabola occurs at the point [latex](0,c)[/latex].
- The vertex depends on the values of a, b, and c. The vertex is [latex]\left(\dfrac{-b}{2a},f\left( \dfrac{-b}{2a}\right)\right)[/latex].
Example
Graph [latex]f(x)=−2x^{2}+3x–3[/latex].Answer: Before making a table of values, look at the values of [latex]a[/latex], [latex]b[/latex] and [latex]c[/latex] to get a general idea of what the graph should look like. [latex]a=−2[/latex], so the graph will open down and be thinner than [latex]f(x)=x^{2}[/latex]. [latex]c=−3[/latex], so it will intersect the y-axis at [latex](0,−3)[/latex]. To find the vertex of the parabola, use the formula [latex] \displaystyle \left( \dfrac{-b}{2a},f\left( \dfrac{-b}{2a} \right) \right)[/latex]. Finding the vertex may make graphing the parabola easier.
[latex]\text{Vertex }\text{formula}=\left( \dfrac{-b}{2a},f\left( \dfrac{-b}{2a} \right) \right)[/latex]
x-coordinate of vertex:[latex] \displaystyle \dfrac{-b}{2a}=\dfrac{-(3)}{2(-2)}=\dfrac{-3}{-4}=\dfrac{3}{4}[/latex]
y-coordinate of vertex:[latex] \displaystyle \begin{array}{l}f\left( \dfrac{-b}{2a} \right)=f\left( \dfrac{3}{4} \right)\\\,\,\,f\left( \dfrac{3}{4} \right)=-2{{\left( \dfrac{3}{4} \right)}^{2}}+3\left( \dfrac{3}{4} \right)-3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-2\left( \dfrac{9}{16} \right)+\dfrac{9}{4}-3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{-18}{16}+\dfrac{9}{4}-3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{-9}{8}+\dfrac{18}{8}-\dfrac{24}{8}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-\dfrac{15}{8}\end{array}[/latex]
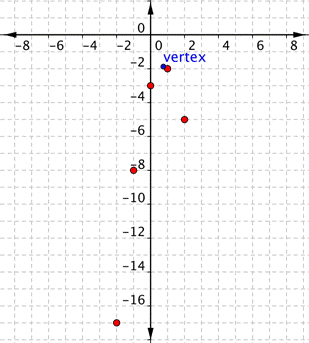
Vertex: [latex] \displaystyle \left( \dfrac{3}{4},-\dfrac{15}{8} \right)[/latex] Use the vertex, [latex] \displaystyle \left( \dfrac{3}{4},-\dfrac{15}{8} \right)[/latex], and the properties you described to get a general idea of the shape of the graph. You can create a table of values to verify your graph. Notice that in this table, the x values increase. The y values increase and then start to decrease again. This indicates a parabola.| x | f(x) |
|---|---|
| [latex]−2[/latex] | [latex]−17[/latex] |
| [latex]−1[/latex] | [latex]−8[/latex] |
| [latex]0[/latex] | [latex]−3[/latex] |
| [latex]1[/latex] | [latex]−2[/latex] |
| [latex]2[/latex] | [latex]−5[/latex] |
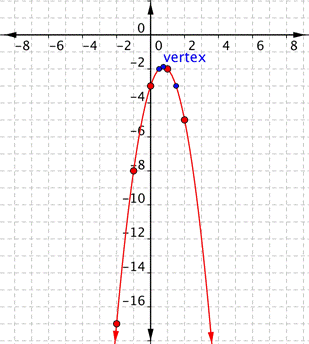
Connect the points as best you can using a smooth curve. Remember that the parabola is two mirror images, so if your points do not have pairs with the same value, you may want to include additional points (such as the ones in blue shown below). Plot points on either side of the vertex.
[latex]x=\dfrac{1}{2}[/latex] and [latex]x=\dfrac{3}{2}[/latex] are good values to include.
Summary
Creating a graph of a function is one way to understand the relationship between the inputs and outputs of that function. Creating a graph can be done by choosing values for x, finding the corresponding y values, and plotting them. However, it helps to understand the basic shape of the function. Knowing how changes to the basic function equation affect the graph is also helpful. The shape of a quadratic function is a parabola. Parabolas have the equation [latex]f(x)=ax^{2}+bx+c[/latex], where a, b, and c are real numbers and [latex]a\ne0[/latex]. The value of a determines the width and the direction of the parabola, while the vertex depends on the values of a, b, and c. The vertex is [latex] \displaystyle \left( \dfrac{-b}{2a},f\left( \dfrac{-b}{2a} \right) \right)[/latex].Contribute!
Licenses & Attributions
CC licensed content, Original
- Graph a Quadratic Function Using a Table of Value and the Vertex. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Unit 17: Functions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
- Ex: Graph a Quadratic Function Using a Table of Values. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
