The Substitution Method
Learning Outcomes
- Use the substitution method to solve systems of equations
- Express the solution of an inconsistent system of equations containing two variables
- Express the solution of a dependent system of equations containing two variables
Solve a system of equations using the substitution method
In the last couple sections, we verified that ordered pairs were solutions to systems, and we used graphs to classify how many solutions a system of two linear equations had. Solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. What if we are not given a point of intersection, or it is not obvious from a graph? Can we still find a solution to the system? Of course you can, using algebra! In this section we will learn the substitution method for finding a solution to a system of linear equations in two variables. We have used substitution in different ways throughout this course. For example, when we were using the formulas for the area of a triangle and simple interest we substituted values that we knew into the formula to solve for values that we did not know. The idea is similar when applied to solving systems, there are just a few different steps in the process. In the substitution method we solve one of the equations for one variable and then substitute the result into the other equation to solve for the second variable. Recall that we can solve for only one variable at a time which is the reason the substitution method is both valuable and practical. Let's start with an example to see what this means.Example
Find the value of [latex]x[/latex] for this system. Equation A: [latex]4x+3y=−14[/latex] Equation B: [latex]y=2[/latex]Answer: The problem asks to solve for [latex]x[/latex]. Equation B gives you the value of [latex]y[/latex], [latex]y=2[/latex], so you can substitute [latex]2[/latex] into Equation A for [latex]y[/latex].
[latex]\begin{array}{r}4x+3y=−14\\y=2\,\,\,\,\,\,\,\end{array}[/latex]
Substitute [latex]y=2[/latex] into Equation A.[latex]4x+3\left(2\right)=−14[/latex]
Simplify and solve the equation for [latex]x[/latex].[latex]\begin{array}{r}4x+6=−14\\4x=−20\\x=−5\,\,\,\end{array}[/latex]
Answer
[latex-display]x=−5[/latex-display]Example
Solve for [latex]x[/latex] and [latex]y[/latex]. Equation A: [latex]y+x=3[/latex] Equation B: [latex]x=y+5[/latex]Answer: The goal of the substitution method is to rewrite one of the equations in terms of a single variable. Equation B tells us that [latex]x=y+5[/latex], so it makes sense to substitute [latex]y+5[/latex] into Equation A for [latex]x[/latex].
[latex]\begin{array}{l}y+x=3\\x=y+5\end{array}[/latex]
Substitute [latex]y+5[/latex] into Equation A for [latex]x[/latex].[latex]\begin{array}{r}y+x=3\\y+\left(y+5\right)=3\end{array}[/latex]
Simplify and solve the equation for [latex]y[/latex].[latex]\begin{array}{r}2y+5=\,\,\,\,3\\\underline{−5\,\,\,\,\,−5}\\2y=−2\\y=−1\end{array}[/latex]
Now find [latex]x[/latex] by substituting this value for [latex]y[/latex] into either equation and solve for [latex]x[/latex]. We will use Equation A here.[latex]\begin{array}{r}y+x=3\\−1+x=3\\\underline{+1\,\,\,\,\,\,\,\,\,+1}\\x=4\end{array}[/latex]
Finally, check the solution [latex]x=4[/latex], [latex]y=−1[/latex] by substituting these values into each of the original equations.[latex]\begin{array}{r}y+x=3\\−1+4=3\\3=3\\\text{TRUE}\end{array}[/latex]
[latex]\begin{array}{l}x=y+5\\4=−1+5\\4=4\\\text{TRUE}\end{array}[/latex]
Answer
[latex-display]x=4[/latex] and [latex]y=−1[/latex-display] The solution is [latex](4,−1)[/latex].Example
Solve the following system of equations by substitution.Answer: First, we will solve the first equation for [latex]y[/latex].
[latex]\begin{array}{llll}-x+y=-5\hfill & \hfill & \hfill & \hfill \\ -\left(8\right)+\left(3\right)=-5\hfill & \hfill & \hfill & \text{True}\hfill \\ 2x - 5y=1\hfill & \hfill & \hfill & \hfill \\ 2\left(8\right)-5\left(3\right)=1\hfill & \hfill & \hfill & \text{True}\hfill \end{array}[/latex]
The substitution method can be used to solve any linear system in two variables, but the method works best if one of the equations contains a coefficient of 1 or [latex]–1[/latex] so that we do not have to deal with fractions.How To: Given a system of two equations in two variables, solve using the substitution method
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, and then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the other variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
Example
Solve for [latex]x[/latex] and [latex]y[/latex].[latex]\begin{array}{l}y = 3x + 6\\−2x + 4y = 4\end{array}[/latex]
Answer: Choose an equation to use for the substitution. The first equation tells you how to express [latex]y[/latex] in terms of [latex]x[/latex], so it makes sense to substitute [latex]3x + 6[/latex] into the second equation for [latex]y[/latex].
[latex]\begin{array}{l}y=3x+6\\−2x+4y=4\end{array}[/latex]
Substitute [latex]3x+6[/latex] for [latex]y[/latex] into the second equation.[latex]\begin{array}{r}−2x+4y=4\\−2x+4\left(3x+6\right)=4\end{array}[/latex]
Simplify and solve the equation for [latex]x[/latex].[latex]\begin{array}{r}−2x+12x+24=4\,\,\,\,\,\,\,\\10x+24=4\,\,\,\,\,\,\,\\\underline{−24\,\,−24\,\,\,\,}\\10x=−20\\x=−2\,\,\,\end{array}[/latex]
To find y, substitute this value for [latex]x[/latex] back into one of the original equations.[latex]\begin{array}{l}y=3x+6\\y=3\left(−2\right)+6\\y =−6+6\\y=0\end{array}[/latex]
Check the solution [latex]x=−2[/latex], [latex]y=0[/latex] by substituting them into each of the original equations.[latex]\begin{array}{l}y=3x+6\\0=3\left(−2\right)+6\\0=−6+6\\0=0\\\text{TRUE}\end{array}[/latex]
[latex]\begin{array}{r}−2x+4y=4\\−2\left(−2\right)+4\left(0\right)=4\\4+0=4\\4=4\\\text{TRUE}\end{array}[/latex]
Answer
[latex-display]x=−2[/latex] and [latex]y=0[/latex-display] The solution is [latex](−2, 0)[/latex].Example
Solve for [latex]x[/latex] and [latex]y[/latex].[latex]\begin{array}{r}2x+3y=22\\3x+y=19\end{array}[/latex]
Answer: Choose an equation to use for the substitution. The second equation, [latex]3x+y=19[/latex], can easily be rewritten in terms of [latex]y[/latex], so it makes sense to start there.
[latex]\begin{array}2x+3y=22\\3x+y=19\end{array}[/latex]
Rewrite [latex]3x+y=19[/latex] in terms of [latex]y[/latex].[latex]\begin{array}3x+y=19\\y=19–3x\end{array}[/latex]
Substitute [latex]19–3x[/latex] for [latex]y[/latex] in the other equation.[latex]\begin{array}{r}2x+3y=22\\2x+3(19–3x)=22\end{array}[/latex]
Simplify and solve the equation for [latex]x[/latex].[latex]\begin{array}{r}2x+57–9x=22\,\,\,\,\\−7x+57=22\,\,\,\,\\−7x=−35\\x=5\,\,\,\,\,\,\,\end{array}[/latex]
Substitute [latex]x=5[/latex] back into one of the original equations to solve for [latex]y[/latex].[latex]\begin{array}{r}3x+y=19\,\,\,\,\,\,\,\,\,\,\,\,\\3\left(5\right)+y=19\,\,\,\,\,\,\,\,\,\,\,\,\\15+y=19\,\,\,\,\,\,\,\,\,\,\,\,\\y=19−15\\y=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]
Check both solutions by substituting them into each of the original equations.[latex]\begin{array}{r}2x+3y=22\\2(5)+3\left(4\right)=22\\10+12=22\\22=22\\\text{TRUE}\\\\3x+y=19\\3\left(5\right)+4= 19\\19=19\\\text{TRUE}\end{array}[/latex]
Answer
[latex-display]x=5[/latex] and [latex]y=4[/latex-display] The solution is [latex](5, 4)[/latex].Try It
[ohm_question]13945[/ohm_question]Identify systems of equations that have no solution or an infinite number of solutions
Recall that an inconsistent system consists of parallel lines that have the same slope but different y-intercepts. They will never intersect. When searching for a solution to an inconsistent system, we will come up with a false statement such as [latex]12=0[/latex]. When we learned methods for solving linear equations in one variable, we found that some equations didn't have any solutions, and others had an infinite number of solutions. We saw this behavior again when we started describing solutions to systems of equations in two variables. Recall this example from Module 1 for solving linear equations in one variable:Solve for [latex]x[/latex]. [latex]12+2x–8=7x+5–5x[/latex]
[latex] \displaystyle \begin{array}{l}12+2x-8=7x+5-5x\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\end{array}[/latex]
[latex]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\\\,\,\,\,\,\,\,\,\underline{-2x\,\,\,\,\,\,\,\,\,\,-2x\,\,\,\,\,\,\,\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4= \,5\end{array}[/latex]
This false statement implies there are no solutions to this equation. In the same way, you may see an outcome like this when you use the substitution method to find a solution to a system of linear equations in two variables. In the next example, you will see an example of a system of two equations that does not have a solution.Example
Solve for [latex]x[/latex] and [latex]y[/latex].[latex]\begin{array}{l}y=5x+4\\10x−2y=4\end{array}[/latex]
Answer: Since the first equation is [latex]y=5x+4[/latex], you can substitute [latex]5x+4[/latex] in for y in the second equation.
[latex]\begin{array}{r}y=5x+4\\10x−2y=4\,\,\,\,\,\,\,\,\,\,\,\,\\10x–2\left(5x+4\right)=4\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]
Expand the expression on the left.[latex]10x–10x–8=4[/latex]
Combine like terms on the left side of equation.[latex]10x–10x=0[/latex], so you are left with [latex]−8=4[/latex].
[latex]\begin{array}{r}0–8=4\\−8=4\end{array}[/latex]
Answer
The statement [latex]−8=4[/latex] is false, so there is no solution.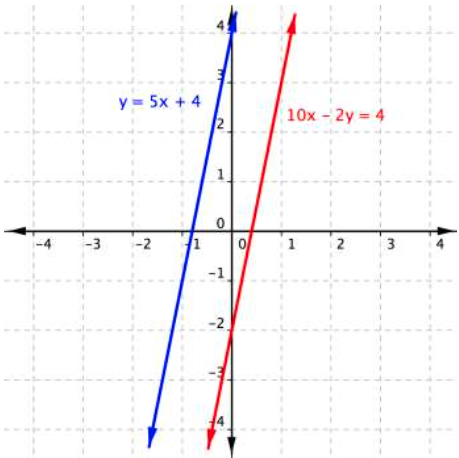 The lines are parallel, they never intersect and there is no solution to this system of linear equations. Note that the result [latex]−8=4[/latex] is not a solution. It is simply a false statement and it indicates that there is no solution.
Let's look at another example in which there is no solution.
The lines are parallel, they never intersect and there is no solution to this system of linear equations. Note that the result [latex]−8=4[/latex] is not a solution. It is simply a false statement and it indicates that there is no solution.
Let's look at another example in which there is no solution.
Example
Solve the following system of equations.[latex]\begin{array}{l}x=9 - 2y\hfill \\ x+2y=13\hfill \end{array}[/latex]
Answer: We can approach this problem in two ways. Because one equation is already solved for x, the most obvious step is to use substitution. We can substitute the expression [latex]9-2y[/latex] for [latex]x[/latex] in the second equation.
[latex]\begin{array}{r}x+2y=13\hfill \\ \left(9 - 2y\right)+2y=13\hfill \\ 9+0y=13\hfill \\ 9=13\hfill \end{array}[/latex]
Clearly, this statement is a contradiction because [latex]9\ne 13[/latex]. Therefore, the system has no solution. The second approach would be to first manipulate the equations so that they are both in slope-intercept form. We manipulate the first equation as follows.[latex]\begin{array}{l}\text{ }x=9 - 2y\hfill \\ 2y=-x+9\hfill \\ \text{ }y=-\dfrac{1}{2}x+\dfrac{9}{2}\hfill \end{array}[/latex]
We then convert the second equation to slope-intercept form.[latex]\begin{array}{l}x+2y=13\hfill \\ \text{ }2y=-x+13\hfill \\ \text{ }y=-\dfrac{1}{2}x+\dfrac{13}{2}\hfill \end{array}[/latex]
Comparing the equations, we see that they have the same slope but different y-intercepts. Therefore, the lines are parallel and do not intersect.[latex]\begin{array}{l}\begin{array}{l}\\ y=-\dfrac{1}{2}x+\dfrac{9}{2}\end{array}\hfill \\ y=-\dfrac{1}{2}x+\dfrac{13}{2}\hfill \end{array}[/latex]
Writing the equations in slope-intercept form confirms that the system is inconsistent because all lines will intersect eventually unless they are parallel. Parallel lines will never intersect; thus, the two lines have no points in common. The graphs of the equations in this example are shown below.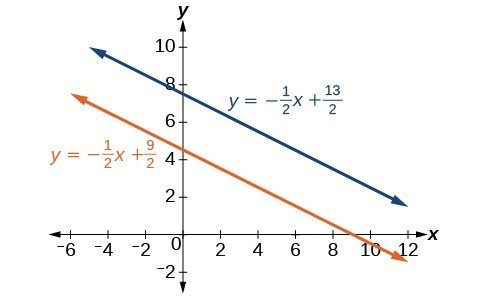
Try It
[ohm_question]115196[/ohm_question]Example
Solve for [latex]x[/latex] and [latex]y[/latex].[latex]\begin{array}{l}\,\,\,y=−0.5x\\9y=−4.5x\end{array}[/latex]
Answer:
Substituting [latex]−0.5x[/latex] for [latex]y[/latex] in the second equation, you find the following: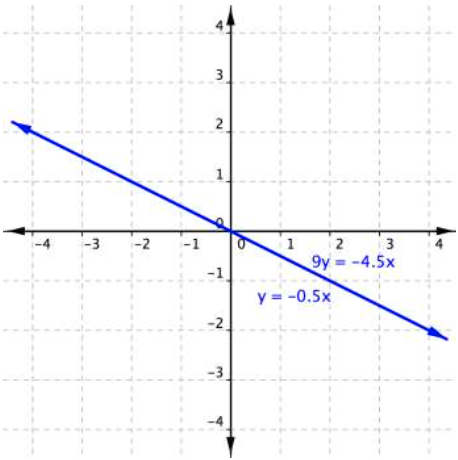 This system consists of two equations that both represent the same line; the two lines are collinear. Every point along the line will be a solution to the system, and that’s why the substitution method yields a true statement. In this case, there are an infinite number of solutions.
This system consists of two equations that both represent the same line; the two lines are collinear. Every point along the line will be a solution to the system, and that’s why the substitution method yields a true statement. In this case, there are an infinite number of solutions.
Try It
[ohm_question]115192[/ohm_question]Summary
The substitution method is one way of solving systems of equations. To use the substitution method, use one equation to find an expression for one of the variables in terms of the other variable. Then substitute that expression in place of that variable in the second equation. You can then solve this equation as it will now have only one variable. Solving using the substitution method will yield one of three results: a single value for each variable within the system (indicating one solution), an untrue statement (indicating no solutions), or a true statement (indicating an infinite number of solutions).Contribute!
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 2: Solve a System of Equations Using Substitution. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex: Solve a System of Equations Using Substitution - Infinite Solutions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex: Solve a System of Equations Using Substitution - No Solution. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: All Rights Reserved.
- Unit 13: Graphing, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
