Why It Matters
Use the concept of instantaneous rate of change of a function from graphical and algebraic points of view to describe and make decisions about situations in accounting, business, and economics
Introduction
In algebra, one of techniques we learned was how to take data and find a function that best models that data. Having a function is one thing, but knowing what that functions tells us is a whole other trick. Let’s say we are given a 12" x 12" sheet of cardboard and told to cut congruent squares out of each corner and then fold up the flaps to make a box.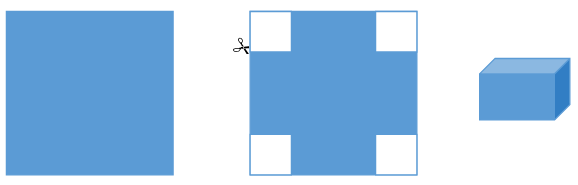 We have a limited supply of cardboard but what we are shipping is flexible and can find in most boxes. We are tasked with finding the maximum volume box that we can create using this method. How would we go about doing that?
We have a limited supply of cardboard but what we are shipping is flexible and can find in most boxes. We are tasked with finding the maximum volume box that we can create using this method. How would we go about doing that?
Learning Outcomes
- Estimate derivatives numerically and graphically
- Distinguish between average and instantaneous rates of change
- Find the slope of the tangent line to the graph of a function at a given point.
- Differentiate basic linear functions
- Differentiate polynomial functions
- Differentiate radical and rational functions
- Differentiate functions using the product, quotient, and chain rules
- Differentiate exponential and logarithmic functions using the product, quotient, and chain rules
- Use the concept of the second derivative to decide whether a situation is changing more quickly or less quickly
Licenses & Attributions
CC licensed content, Original
- Provided by: Columbia Basin College Authored by: Paul Jones. License: CC BY: Attribution.
