We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Business Calculus

Reading: Concept of Derivative

Precalculus Idea: Slope and Rate of Change

The slope of a line measures how fast a line rises or falls as we move from left to right along the line. It measures the rate of change of the y-coordinate with respect to changes in the x-coordinate. If the line represents the distance traveled over time, for example, then its slope represents the velocity. In figure 1, you can remind yourself of how we calculate slope using two points on the line: m = { slope from P to Q } = [latex] \frac{\text {rise}}{\text {run}} [/latex] = [latex] \frac{y_2 - y_1}{x_2 - x_1} [/latex] = [latex] \frac{\Delta y}{\Delta x} [/latex]
Fig_1_1_1 Figure 1
We would like to be able to get that same sort of information (how fast the curve rises or falls, velocity from distance) even if the graph is not a straight line. But what happens if we try to find the slope of a curve, as in figure 2? We need two points in order to determine the slope of a line. How can we find a slope of a curve, at just one point?
Figure 2 Figure 2
The answer, as suggested in Figure 2 is to find the slope of the tangent line to the curve at that point. Most of us have an intuitive idea of what a tangent line is. Unfortunately, “tangent line” is hard to define precisely. Definition: A secant line is a line between two points on a curve. Can’t-quite-do-it-yet Definition: A tangent line is a line at one point on a curve . . . that does its best to be the curve at that point? It turns out that the easiest way to define the tangent line is to define its slope.

Definition of the Derivative

The tangent line problem and the instantaneous velocity problem are the same problem. In each problem we wanted to know how rapidly something was changing at an instant in time, and the answer turned out to be finding the slope of a tangent line, which we approximated with the slope of a secant line. This idea is the key to defining the slope of a curve.

The Derivative

  • The derivative of a function f at a point (x, f(x)) is the instantaneous rate of change.
  • The derivative is the slope of the tangent line to the graph of f at the point (x, f(x)).
  • The derivative is the slope of the curve f(x) at the point (x, f(x)).
  • A function is called differentiable at (x, f(x)) if its derivative exists at (x, f(x)).

Notation for the Derivative

The derivative of y = f(x) with respect to x is written as [latex] f\prime(x) [/latex] (read aloud as “f prime of  x”), or [latex] y\prime [/latex] (“y prime”) or [latex] \frac{dy}{dx} [/latex] (read aloud as “dee why dee ex”), or [latex] \frac{df}{dx} [/latex] The notation that resembles a fraction is called Leibniz notation. It displays not only the name of the function (f or y), but also the name of the variable (in this case, x). It looks like a fraction because the derivative is a slope. In fact, this is simply [latex] \frac{\Delta y}{\Delta x} [/latex], written in Roman letters instead of Greek letters.

Verb Forms

We find the derivative of a function, or take the derivative of a function, or differentiate a function. We use an adaptation of the [latex] \frac{dy}{dx} [/latex] notation to mean “find the derivative of f(x):” [latex-display] \frac{d}{dx} {(f(x))} = \frac{df}{dx} [/latex-display]

Formal Algebraic Definition

[latex-display]\displaystyle{f'}{(x)}=\lim{h\to 0}\frac{{f(x+h)-f(x)}}{{h}}[/latex-display]

Practical Definition

The derivative can be approximated by looking at an average rate of change, or the slope of a secant line, over a very tiny interval. The tinier the interval, the closer this is to the true instantaneous rate of change, slope of the tangent line, or slope of the curve.

Looking Ahead

We will have methods for computing exact values of derivatives from formulas soon. If the function is given to you as a table or graph, you will still need to approximate this way. This is the foundation for the rest of this chapter. It’s remarkable that such a simple idea (the slope of a tangent line) and such a simple definition (for the derivative f′) will lead to so many important ideas and applications.

The Derivative as a Function

We now know how to find (or at least approximate) the derivative of a function for any x-value; this means we can think of the derivative as a function, too. The inputs are the same xs; the output is the value of the derivative at

Example

Figure 3 Figure 3
Figure 3 is the graph of a function y = f(x). We can use the information in the graph to fill in a table showing values of f′(x): At various values of x, draw your best guess at the tangent line and measure its slope. You might have to extend your lines so you can read some points. In general, your estimate of the slope will be better if you choose points that are easy to read and far away from each other. Here are my estimates for a few values of x (parts of the tangent lines I used are shown):
 x y = f(x) f′(x) = the estimated SLOPE of the tangent line to the curve at the point (x, y).
0 0 1
1 1 0
2 0 −1
3 −1 0
4 1 1
5 2 0.5
We can estimate the values of f′(x) at some non-integer values of x, too: f′(.5) ≈ 0.5 and f′(1.3) ≈ –0.3. We can even think about entire intervals. For example, if 0 < x < 1, then f(x) is increasing, all the slopes are positive, and so f′(x) is positive. The values of f′(x) definitely depend on the values of x , and f′(x) is a function of x. We can use the results in the table to help sketch the graph of f′(x) in figure 4.
Figure 4 Figure 4

Example

Figure 5 is the graph of the height h(t) of a rocket at time t. Sketch the graph of the velocity of the rocket at time t. (Velocity is the derivative of the height function, so it is the slope of the tangent to the graph of position or height.)
Figure 5 Figure 5

Solution

Figure 6 shows the velocity of the rocket. This is v(t) = h′(t).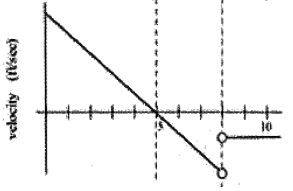
Fig_1_1_6 Figure 6

Licenses & Attributions

CC licensed content, Shared previously

  • Business Calculus. Provided by: Washington State Colleges Authored by: Dale Hoffman and Shana Calaway. Located at: https://docs.google.com/file/d/0B1lkHWwO61QEM0gwOFhES2N5Tlk/edit. License: CC BY: Attribution.