We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Solutions

Solutions to Try Its

1. x-intercept is [latex]\left(4,0\right)[/latex]; y-intercept is [latex]\left(0,3\right)[/latex]. This is an image of a line graph on an x, y coordinate plane. The x and y axes range from negative 4 to 6. The function y = -3x/4 + 3 is plotted. 2. [latex]\left(-5,\frac{5}{2}\right)[/latex]

Solutions to Odd-Numbered Exercises

1. Answers may vary. Yes. It is possible for a point to be on the x-axis or on the y-axis and therefore is considered to NOT be in one of the quadrants. 3. The y-intercept is the point where the graph crosses the y-axis. 5. The x-intercept is [latex]\left(2,0\right)[/latex] and the y-intercept is [latex]\left(0,6\right)[/latex]. 7. The x-intercept is [latex]\left(2,0\right)[/latex] and the y-intercept is [latex]\left(0,-3\right)[/latex]. 9. The x-intercept is [latex]\left(3,0\right)[/latex] and the y-intercept is [latex]\left(0,\frac{9}{8}\right)[/latex]. 11. [latex]y=4 - 2x[/latex] 13. [latex]y=\frac{5 - 2x}{3}[/latex] 15. [latex]y=2x-\frac{4}{5}[/latex] 17. [latex]d=\sqrt{74}[/latex] 19. [latex]d=\sqrt{36}=6[/latex] 21. [latex]d\approx 62.97[/latex] 23. [latex]\left(3,\frac{-3}{2}\right)[/latex] 25. [latex]\left(2,-1\right)[/latex] 27. [latex]\left(0,0\right)[/latex] 29. [latex]y=0[/latex] 31. not collinear This is an image of an x, y coordinate plane with the x and y axes ranging from negative 5 to 5. The points (0,4); (-1,2) and (2,1) are plotted and labeled. 33. [latex]\left(-3,2\right),\left(1,3\right),\left(4,0\right)[/latex] 35.
[latex]x[/latex] [latex]y[/latex]
[latex]-3[/latex] 1
0 2
3 3
6 4
This is an image of an x, y coordinate plane with the x and y axes ranging from negative 10 to 10. The points (-3, 1); (0, 2); (3, 3) and (6, 4) are plotted and labeled. A line runs through all these points. 37.
x y
–3 0
0 1.5
3 3
This is an image of an x, y coordinate plane with the x and y axes ranging from negative 10 to 10. The points (-3, 0); (0, 1.5) and (3, 3) are plotted and labeled. A line runs through all of these points. 39. This is an image of an x, y coordinate plane with the x and y axes ranging from negative 10 to 10. The points (8, 0) and (0, -4) are plotted and labeled. A line runs through both of these points. 41. This is an image of an x, y coordinate plane with the x and y axes ranging from negative 10 to 10. The points (0, 2) and (3, 0) are plotted and labeled. A line runs through both of these points. 43. [latex]d=8.246[/latex] 45. [latex]d=5[/latex] 47. [latex]\left(-3,4\right)[/latex] 49. [latex]x=0\text{ }y=-2[/latex] 51. [latex]x=0.75\text{ }y=0[/latex] 53. [latex]x=-1.667\text{ }y=0[/latex] 55. [latex]\text{15}\text{-11}.\text{2 }=\text{ 3}.8[/latex] mi shorter 57. [latex]\text{6}.0\text{42}[/latex] 59. Midpoint of each diagonal is the same point [latex]\left(2,2\right)[/latex]. Note this is a characteristic of rectangles, but not other quadrilaterals. 61. [latex]\text{37}[/latex] mi 63. 54 ft 65. 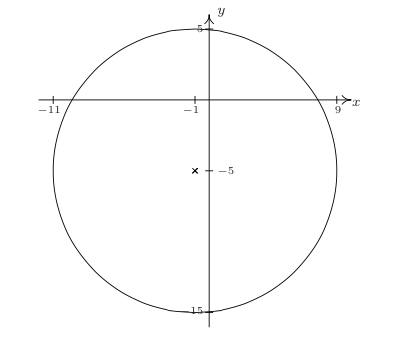[latex]{\left(x+1\right)}^{2}+{\left(y+5\right)}^{2}=100\\[/latex]   Graph of a circle on the cartesian coordinate axes passing through the points (0,5) and (0,-15) 67. [latex]{\left(x+3\right)}^{2}+{\left(y-\frac{7}{13}\right)}^{2}=\frac{1}{4}\\[/latex] 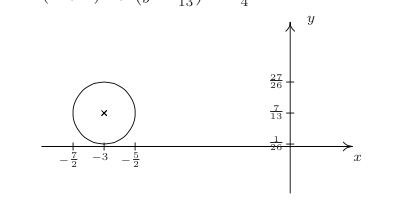Graph of circle on cartesian coordinate axes whose center is at (-3, 7/13) 69. [latex]{\left(x+e\right)}^{2}+{\left(y-\sqrt{2}\right)}^{2}={\pi}^{2}\\[/latex] 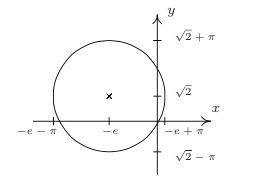Graph of a circle on the cartesian coordinate plane with center at (-e, square root of two), and passing through the origin. 71. [latex]{\left(x-2\right)}^{2}+{\left(y-5\right)}^{2}=4\\[/latex], Center (2,-5), radius r = 2 73. [latex]{\left(x+4\right)}^{2}+{\left(y-5\right)}^{2}=42\\[/latex], Center (-4,5), radius r = [latex]\sqrt{42}\\[/latex] 75. [latex]{\left(x\right)}^{2}+{\left(y-3\right)}^{2}=0\\[/latex], This is not a circle 77. [latex]{\left(x-3\right)}^{2}+{\left(y-5\right)}^{2}=65\\[/latex] 79. [latex]{\left(x-1\right)}^{2}+{\left(y-5\right)}^{2}=5\\[/latex] 81. [latex]{\left(x\right)}^{2}+{\left(y-72\right)}^{2}=4096\\[/latex]