We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > MATH 1314: College Algebra

Find the equation of an exponential function

In the previous examples, we were given an exponential function, which we then evaluated for a given input. Sometimes we are given information about an exponential function without knowing the function explicitly. We must use the information to first write the form of the function, then determine the constants a and b, and evaluate the function.

How To: Given two data points, write an exponential model.

  1. If one of the data points has the form [latex]\left(0,a\right)\\[/latex], then a is the initial value. Using a, substitute the second point into the equation [latex]f\left(x\right)=a{\left(b\right)}^{x}\\[/latex], and solve for b.
  2. If neither of the data points have the form [latex]\left(0,a\right)\\[/latex], substitute both points into two equations with the form [latex]f\left(x\right)=a{\left(b\right)}^{x}\\[/latex]. Solve the resulting system of two equations in two unknowns to find a and b.
  3. Using the a and b found in the steps above, write the exponential function in the form [latex]f\left(x\right)=a{\left(b\right)}^{x}\\[/latex].

Example 3: Writing an Exponential Model When the Initial Value Is Known

In 2006, 80 deer were introduced into a wildlife refuge. By 2012, the population had grown to 180 deer. The population was growing exponentially. Write an algebraic function N(t) representing the population N of deer over time t.

Solution

We let our independent variable t be the number of years after 2006. Thus, the information given in the problem can be written as input-output pairs: (0, 80) and (6, 180). Notice that by choosing our input variable to be measured as years after 2006, we have given ourselves the initial value for the function, a = 80. We can now substitute the second point into the equation [latex]N\left(t\right)=80{b}^{t}\\[/latex] to find b:

[latex]\begin{cases}N\left(t\right)\hfill & =80{b}^{t}\hfill & \hfill \\ 180\hfill & =80{b}^{6}\hfill & \text{Substitute using point }\left(6, 180\right).\hfill \\ \frac{9}{4}\hfill & ={b}^{6}\hfill & \text{Divide and write in lowest terms}.\hfill \\ b\hfill & ={\left(\frac{9}{4}\right)}^{\frac{1}{6}}\hfill & \text{Isolate }b\text{ using properties of exponents}.\hfill \\ b\hfill & \approx 1.1447 & \text{Round to 4 decimal places}.\hfill \end{cases}\\[/latex]

NOTE: Unless otherwise stated, do not round any intermediate calculations. Then round the final answer to four places for the remainder of this section.

The exponential model for the population of deer is [latex]N\left(t\right)=80{\left(1.1447\right)}^{t}\\[/latex]. (Note that this exponential function models short-term growth. As the inputs gets large, the output will get increasingly larger, so much so that the model may not be useful in the long term.)

We can graph our model to observe the population growth of deer in the refuge over time. Notice that the graph below passes through the initial points given in the problem, [latex]\left(0,\text{ 8}0\right)\\[/latex] and [latex]\left(\text{6},\text{ 18}0\right)\\[/latex]. We can also see that the domain for the function is [latex]\left[0,\infty \right)\\[/latex], and the range for the function is [latex]\left[80,\infty \right)\\[/latex].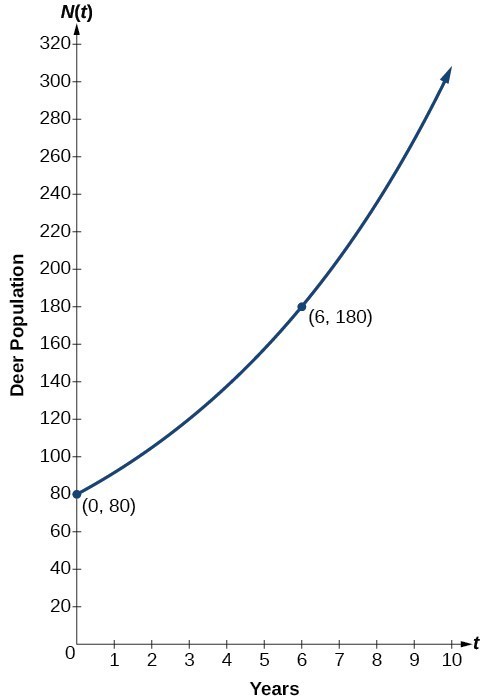 Graph of the exponential function, N(t) = 80(1.1447)^t, with labeled points at (0, 80) and (6, 180).

Figure 3. Graph showing the population of deer over time, [latex]N\left(t\right)=80{\left(1.1447\right)}^{t}\\[/latex], t years after 2006

Try It 3

A wolf population is growing exponentially. In 2011, 129 wolves were counted. By 2013 the population had reached 236 wolves. What two points can be used to derive an exponential equation modeling this situation? Write the equation representing the population N of wolves over time t.

Solution

Example 4: Writing an Exponential Model When the Initial Value is Not Known

Find an exponential function that passes through the points [latex]\left(-2,6\right)\\[/latex] and [latex]\left(2,1\right)\\[/latex].

Solution

Because we don’t have the initial value, we substitute both points into an equation of the form [latex]f\left(x\right)=a{b}^{x}\\[/latex], and then solve the system for a and b.

  • Substituting [latex]\left(-2,6\right)\\[/latex] gives [latex]6=a{b}^{-2}\\[/latex]
  • Substituting [latex]\left(2,1\right)\\[/latex] gives [latex]1=a{b}^{2}\\[/latex]

Use the first equation to solve for a in terms of b: Take 6 equals ab to the negative 2 power. Divide. Use properties of exponents to rewrite the denominator.

Substitute a in the second equation, and solve for b: Substitute a. Use properties of exponents to isolate b. Round 4 decimal places.

Use the value of b in the first equation to solve for the value of a: A is equal to 6b squared is approximately 6 times zero point 6 3 8 9 squared is approximately 2.4492.

Thus, the equation is [latex]f\left(x\right)=2.4492{\left(0.6389\right)}^{x}\\[/latex].

We can graph our model to check our work. Notice that the graph below passes through the initial points given in the problem, [latex]\left(-2,\text{ 6}\right)\\[/latex] and [latex]\left(2,\text{ 1}\right)\\[/latex]. The graph is an example of an exponential decay function.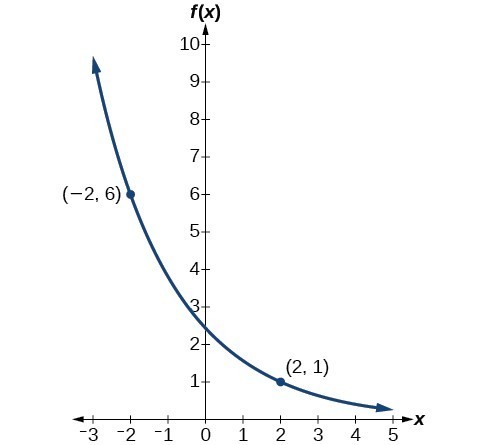 Graph of the exponential function, f(x)=2.4492(0.6389)^x, with labeled points at (-2, 6) and (2, 1).

Figure 4. The graph of [latex]f\left(x\right)=2.4492{\left(0.6389\right)}^{x}\\[/latex] models exponential decay.

Try It 4

Given the two points [latex]\left(1,3\right)\\[/latex] and [latex]\left(2,4.5\right)\\[/latex], find the equation of the exponential function that passes through these two points.

Solution

Q & A

Do two points always determine a unique exponential function?

Yes, provided the two points are either both above the x-axis or both below the x-axis and have different x-coordinates. But keep in mind that we also need to know that the graph is, in fact, an exponential function. Not every graph that looks exponential really is exponential. We need to know the graph is based on a model that shows the same percent growth with each unit increase in x, which in many real world cases involves time.

How To: Given the graph of an exponential function, write its equation.

  1. First, identify two points on the graph. Choose the y-intercept as one of the two points whenever possible. Try to choose points that are as far apart as possible to reduce round-off error.
  2. If one of the data points is the y-intercept [latex]\left(0,a\right)\\[/latex] , then a is the initial value. Using a, substitute the second point into the equation [latex]f\left(x\right)=a{\left(b\right)}^{x}\\[/latex], and solve for b.
  3. If neither of the data points have the form [latex]\left(0,a\right)\\[/latex], substitute both points into two equations with the form [latex]f\left(x\right)=a{\left(b\right)}^{x}\\[/latex]. Solve the resulting system of two equations in two unknowns to find a and b.
  4. Write the exponential function, [latex]f\left(x\right)=a{\left(b\right)}^{x}\\[/latex].

Example 5: Writing an Exponential Function Given Its Graph

Find an equation for the exponential function graphed in Figure 5.

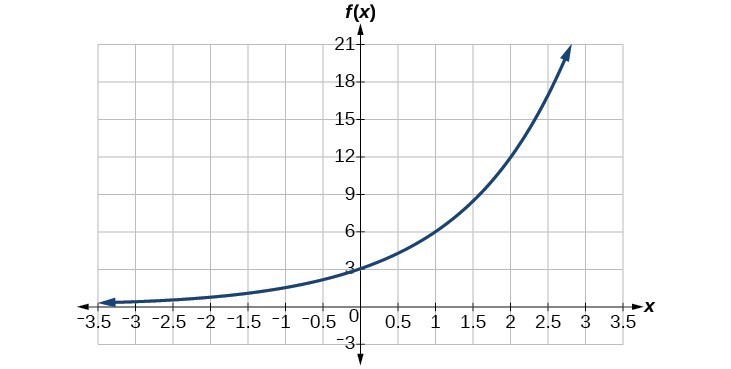Graph of an increasing exponential function with notable points at (0, 3) and (2, 12).Figure 5

Solution

We can choose the y-intercept of the graph, [latex]\left(0,3\right)\\[/latex], as our first point. This gives us the initial value, [latex]a=3\\[/latex]. Next, choose a point on the curve some distance away from [latex]\left(0,3\right)\\[/latex] that has integer coordinates. One such point is [latex]\left(2,12\right)\\[/latex].

[latex]\begin{cases}y=a{b}^{x}& \text{Write the general form of an exponential equation}. \\ y=3{b}^{x} & \text{Substitute the initial value 3 for }a. \\ 12=3{b}^{2} & \text{Substitute in 12 for }y\text{ and 2 for }x. \\ 4={b}^{2} & \text{Divide by 3}. \\ b=\pm 2 & \text{Take the square root}.\end{cases}\\[/latex]

Because we restrict ourselves to positive values of b, we will use b = 2. Substitute a and b into the standard form to yield the equation [latex]f\left(x\right)=3{\left(2\right)}^{x}\\[/latex].

Try It 5

Find an equation for the exponential function graphed in Figure 6.

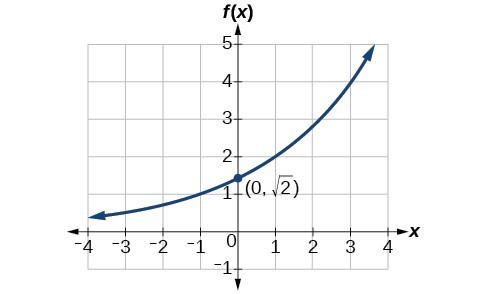Graph of an increasing function with a labeled point at (0, sqrt(2)).Figure 6
Solution

How To: Given two points on the curve of an exponential function, use a graphing calculator to find the equation.

  1. Press [STAT].
  2. Clear any existing entries in columns L1 or L2.
  3. In L1, enter the x-coordinates given.
  4. In L2, enter the corresponding y-coordinates.
  5. Press [STAT] again. Cursor right to CALC, scroll down to ExpReg (Exponential Regression), and press [ENTER].
  6. The screen displays the values of a and b in the exponential equation [latex]y=a\cdot {b}^{x}\\[/latex].

Example 6: Using a Graphing Calculator to Find an Exponential Function

Use a graphing calculator to find the exponential equation that includes the points [latex]\left(2,24.8\right)\\[/latex] and [latex]\left(5,198.4\right)\\[/latex].

Solution

Follow the guidelines above. First press [STAT], [EDIT], [1: Edit…], and clear the lists L1 and L2. Next, in the L1 column, enter the x-coordinates, 2 and 5. Do the same in the L2 column for the y-coordinates, 24.8 and 198.4.

Now press [STAT], [CALC], [0: ExpReg] and press [ENTER]. The values a = 6.2 and b = 2 will be displayed. The exponential equation is [latex]y=6.2\cdot {2}^{x}\\[/latex].

Try It 6

Use a graphing calculator to find the exponential equation that includes the points (3, 75.98) and (6, 481.07).

Solution

Licenses & Attributions

CC licensed content, Shared previously

  • Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..