Putting It Together: Exponential and Logarithmic Equations and Models
At the start of this module, you were assigned the task of analyzing a fossilized bone to determine its age. To make that estimate, you need to model for the decay rate of carbon-14. The decay of a radioactive element is an exponential function of the form:where,
[latex]A(t)[/latex] = mass of element remaining after t years
[latex]A_0[/latex] = original mass of element
[latex]k[/latex] = rate of decay
[latex]t[/latex] = time in years
So to create a model for the decay function of carbon-14, assume for simplicity that the sample you started with had a mass of 1g. We know that half the starting mass of the sample will remain after one half-life, which is 5,730 years. We can substitute these values for [latex]A(t)[/latex], and [latex]A_0[/latex] as follows:[latex]A\left(t\right)=A_0e^{-kt}[/latex]
[latex]\frac{1}{2}=(1)e^{-k\left(5730\right)}[/latex]
[latex]1n\left(\frac{1}{2}\right)=1n\left(e^{-k\left(5730\right)}\right)[/latex]
[latex]1n\left(2^{-1}\right)=\left(-5730k\right)1n\left(e\right)[/latex]
[latex]-1n\left(2\right)=-5730k\left(1\right)[/latex]
[latex]k\approx1.21\times10^{-4}[/latex]
Now you know the decay rate so you can write the equation for the exponential decay of carbon-14, and you can represent it as a graph.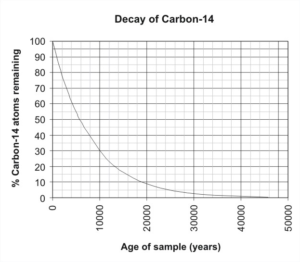
The next step is to evaluate the function for a given mass. Assume a starting mass of 100 grams, and that there are 20 grams remaining. Substitute these values into the model in the following way:
| Write the equation | [latex]A(t)=100e^{\large{-(0.000121)t}}[/latex] |
| Substitute 20 grams for A(t) | [latex]20=100e^{\large{-\left(0.000121\right)t}}[/latex] |
| Divide both sides by 100 | [latex]0.20=e^{\large{-\left(0.000121\right)t}}[/latex] |
| Change into logarithmic form | [latex]1n\left(0.20\right)=-\left(0.000121\right)t[/latex] |
| Divide both sides by -0.000121 | [latex]t={\large\frac{1n\left(0.20\right)}{-0.000121}}[/latex] |
| Solve | [latex]t\approx13,301[/latex] years |
[latex]A\left(t\right)=100e^{-\left(0.000121\right)t}[/latex]
[latex]A\left(8000\right)=100e^{-\left(0.000121\right)\left(8000\right)}\approx38[/latex] grams
About 38 grams would remain after 8,000 years. Understanding exponential functions help scientists better understand radioactive decay and provide insights into past civilizations and species.Licenses & Attributions
CC licensed content, Original
- Putting It Together: Exponential and Logarithmic Equations and Models. Authored by: Lumen Learning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Radioactive decay of carbon-14. Located at: https://commons.wikimedia.org/wiki/File:Radioactive_decay_of_Carbon-14.png#/media/File:Radioactive_decay_of_Carbon-14.png. License: CC BY-SA: Attribution-ShareAlike.
