We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

The Substitution and Addition Methods

Learning Objectives

  • Use the substitution method to find solution(s) to a system of two linear equations
  • Use the addition method to find solution(s) to a system of linear equations

Solving Systems of Equations by Substitution

Solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. We will consider two more methods of solving a system of linear equations that are more precise than graphing. One such method is solving a system of equations by the substitution method, in which we solve one of the equations for one variable and then substitute the result into the second equation to solve for the second variable. Recall that we can solve for only one variable at a time, which is the reason the substitution method is both valuable and practical.

How To: Given a system of two equations in two variables, solve using the substitution method.

  1. Solve one of the two equations for one of the variables in terms of the other.
  2. Substitute the expression for this variable into the second equation, then solve for the remaining variable.
  3. Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
  4. Check the solution in both equations.

Example: Solving a System of Equations in Two Variables by Substitution

Solve the following system of equations by substitution. [latex-display]\begin{array}{l}\text{ }-x+y=-5\hfill \\ \text{ }2x - 5y=1\hfill \end{array}[/latex-display]

Answer: First, we will solve the first equation for [latex]y[/latex]. [latex-display]\begin{array}{l}-x+y=-5\hfill \\ \text{ }y=x - 5\hfill \end{array}[/latex-display] Now we can substitute the expression [latex]x - 5[/latex] for [latex]y[/latex] in the second equation. [latex-display]\begin{array}{l}\text{ }2x - 5y=1\hfill \\ 2x - 5\left(x - 5\right)=1\hfill \\ \text{ }2x - 5x+25=1\hfill \\ \text{ }-3x=-24\hfill \\ \text{ }x=8\hfill \end{array}[/latex-display] Now, we substitute [latex]x=8[/latex] into the first equation and solve for [latex]y[/latex]. [latex-display]\begin{array}{l}-\left(8\right)+y=-5\hfill \\ \text{ }y=3\hfill \end{array}[/latex-display] Our solution is [latex]\left(8,3\right)[/latex]. Check the solution by substituting [latex]\left(8,3\right)[/latex] into both equations. [latex-display]\begin{array}{llll}-x+y=-5\hfill & \hfill & \hfill & \hfill \\ -\left(8\right)+\left(3\right)=-5\hfill & \hfill & \hfill & \text{True}\hfill \\ 2x - 5y=1\hfill & \hfill & \hfill & \hfill \\ 2\left(8\right)-5\left(3\right)=1\hfill & \hfill & \hfill & \text{True}\hfill \end{array}[/latex-display]

Try It

You can use Desmos to help you solve a system of equations by substitution. We will use the following system to show you how: [latex-display]\begin{array}{l}x=y+3\hfill \\ 4=3x - 2y\hfill \end{array}[/latex-display] First, solve both equations for y: [latex-display]\begin{array}{l}y=x-3\hfill \\ y=\frac{3}{2}x - 2\hfill \end{array}[/latex-display] Now enter [latex]x-3=\frac{3}{2}x - 2[/latex] into Desmos. You will see that Desmos has provided you with [latex]x = -2[/latex]. You now can substitute [latex]x = -2[/latex] into both equations.  If you get the same result for both, you have found an ordered pair solution. Give it a try.

Answer: [latex]\left(-2,-5\right)[/latex]

Q & A

Can the substitution method be used to solve any linear system in two variables?

Yes, but the method works best if one of the equations contains a coefficient of 1 or –1 so that we do not have to deal with fractions.
 

Solving Systems of Equations in Two Variables by the Addition Method

A third method of solving systems of linear equations is the addition method, this method is also called the elimination method. In this method, we add two terms with the same variable, but opposite coefficients, so that the sum is zero. Of course, not all systems are set up with the two terms of one variable having opposite coefficients. Often we must adjust one or both of the equations by multiplication so that one variable will be eliminated by addition.

How To: Given a system of equations, solve using the addition method.

  1. Write both equations with x- and y-variables on the left side of the equal sign and constants on the right.
  2. Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
  3. Solve the resulting equation for the remaining variable.
  4. Substitute that value into one of the original equations and solve for the second variable.
  5. Check the solution by substituting the values into the other equation.

Example: Solving a System by the Addition Method

Solve the given system of equations by addition. [latex-display]\begin{array}{l}x+2y=-1\hfill \\ -x+y=3\hfill \end{array}[/latex-display]

Answer: Both equations are already set equal to a constant. Notice that the coefficient of [latex]x[/latex] in the second equation, –1, is the opposite of the coefficient of [latex]x[/latex] in the first equation, 1. We can add the two equations to eliminate [latex]x[/latex] without needing to multiply by a constant. [latex-display]\frac{\begin{array}{l}\hfill \\ x+2y=-1\hfill \\ -x+y=3\hfill \end{array}}{\text{}\text{}\text{}\text{}\text{}3y=2}[/latex-display] Now that we have eliminated [latex]x[/latex], we can solve the resulting equation for [latex]y[/latex]. [latex-display]\begin{array}{l}3y=2\hfill \\ \text{ }y=\frac{2}{3}\hfill \end{array}[/latex-display] Then, we substitute this value for [latex]y[/latex] into one of the original equations and solve for [latex]x[/latex]. [latex-display]\begin{array}{l}\text{ }-x+y=3\hfill \\ \text{ }-x+\frac{2}{3}=3\hfill \\ \text{ }-x=3-\frac{2}{3}\hfill \\ \text{ }-x=\frac{7}{3}\hfill \\ \text{ }x=-\frac{7}{3}\hfill \end{array}[/latex-display] The solution to this system is [latex]\left(-\frac{7}{3},\frac{2}{3}\right)[/latex]. Check the solution in the first equation. [latex-display]\begin{array}{llll}\text{ }x+2y=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }\left(-\frac{7}{3}\right)+2\left(\frac{2}{3}\right)=\hfill & \hfill & \hfill & \hfill \\ \text{ }-\frac{7}{3}+\frac{4}{3}=\hfill & \hfill & \hfill & \hfill \\ \text{ }-\frac{3}{3}=\hfill & \hfill & \hfill & \hfill \\ \text{ }-1=-1\hfill & \hfill & \hfill & \text{True}\hfill \end{array}[/latex-display]

Analysis of the Solution

We gain an important perspective on systems of equations by looking at the graphical representation. See the graph below to find that the equations intersect at the solution. We do not need to ask whether there may be a second solution because observing the graph confirms that the system has exactly one solution.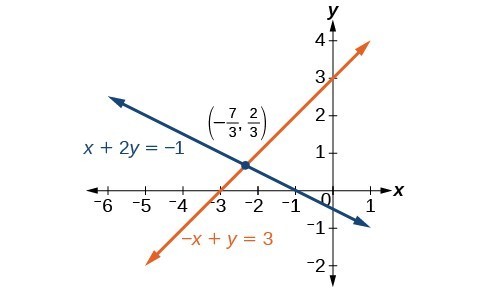 A graph of two lines that cross at the point negative seven-thirds, two-thirds. The first line's equation is x+2y=negative 1. The second line's equation is negative x + y equals 3.

Example: Using the Addition Method When Multiplication of One Equation Is Required

Solve the given system of equations by the addition method. [latex-display]\begin{array}{l}3x+5y=-11\hfill \\ \hfill \\ x - 2y=11\hfill \end{array}[/latex-display]

Answer: Adding these equations as presented will not eliminate a variable. However, we see that the first equation has [latex]3x[/latex] in it and the second equation has [latex]x[/latex]. So if we multiply the second equation by [latex]-3,\text{}[/latex] the x-terms will add to zero. [latex-display]\begin{array}{llll}\text{ }x - 2y=11\hfill & \hfill & \hfill & \hfill \\ -3\left(x - 2y\right)=-3\left(11\right)\hfill & \hfill & \hfill & \text{Multiply both sides by }-3.\hfill \\ \text{ }-3x+6y=-33\hfill & \hfill & \hfill & \text{Use the distributive property}.\hfill \end{array}[/latex-display] Now, let’s add them. [latex-display]\begin{array}\ \hfill 3x+5y=−11 \\ \hfill −3x+6y=−33 \\ \text{_____________} \\ \hfill 11y=−44 \\ \hfill y=−4 \end{array}[/latex-display] For the last step, we substitute [latex]y=-4[/latex] into one of the original equations and solve for [latex]x[/latex]. [latex-display]\begin{array}{c}3x+5y=-11\\ 3x+5\left(-4\right)=-11\\ 3x - 20=-11\\ 3x=9\\ x=3\end{array}[/latex-display] Our solution is the ordered pair [latex]\left(3,-4\right)[/latex]. Check the solution in the original second equation. 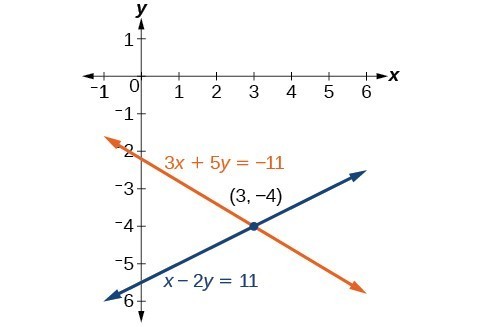[latex-display]\begin{array}{llll}\text{ }x - 2y=11\hfill & \hfill & \hfill & \hfill \\ \left(3\right)-2\left(-4\right)=3+8\hfill & \hfill & \hfill & \hfill \\ \text{ }=11\hfill & \hfill & \hfill & \text{True}\hfill \end{array}[/latex-display] A graph of two lines that cross at the point 3, negative 4. The first line's equation is 3x+5y=-11. The second line's equation is x-2y=11.

Try It

Solve the system of equations by addition. [latex-display]\begin{array}{c}2x - 7y=2\\ 3x+y=-20\end{array}[/latex-display]

Answer: [latex]\left(-6,-2\right)[/latex]

Example: Using the Addition Method When Multiplication of Both Equations Is Required

Solve the given system of equations in two variables by addition. [latex-display]\begin{array}{c}2x+3y=-16\\ 5x - 10y=30\end{array}[/latex-display]

Answer: One equation has [latex]2x[/latex] and the other has [latex]5x[/latex]. The least common multiple is [latex]10x[/latex] so we will have to multiply both equations by a constant in order to eliminate one variable. Let’s eliminate [latex]x[/latex] by multiplying the first equation by [latex]-5[/latex] and the second equation by [latex]2[/latex]. [latex-display]\begin{array}{l} -5\left(2x+3y\right)=-5\left(-16\right)\hfill \\ \text{ }-10x - 15y=80\hfill \\ \text{ }2\left(5x - 10y\right)=2\left(30\right)\hfill \\ \text{ }10x - 20y=60\hfill \end{array}[/latex-display] Then, we add the two equations together. [latex-display]\begin{array}\ −10x−15y=80 \\ 10x−20y=60 \\ \text{______________} \\ \text{ }−35y=140 \\ y=−4 \end{array}[/latex-display] Substitute [latex]y=-4[/latex] into the original first equation. [latex-display]\begin{array}{c}2x+3\left(-4\right)=-16\\ 2x - 12=-16\\ 2x=-4\\ x=-2\end{array}[/latex-display] The solution is [latex]\left(-2,-4\right)[/latex]. Check it in the other equation. [latex-display]\begin{array}{r}\hfill \text{ }5x - 10y=30\\ \hfill 5\left(-2\right)-10\left(-4\right)=30\\ \hfill \text{ }-10+40=30\\ \hfill \text{ }30=30\end{array}[/latex-display] A graph of two lines that cross the point -2,-4. The first line's equation is 2x+3y=-16. The second line's equation is 5x-10y=30.

Example: Using the Addition Method in Systems of Equations Containing Fractions

Solve the given system of equations in two variables by addition. [latex-display]\begin{array}{l}\frac{x}{3}+\frac{y}{6}=3\hfill \\ \frac{x}{2}-\frac{y}{4}=\text{ }1\hfill \end{array}[/latex-display]

Answer: First clear each equation of fractions by multiplying both sides of the equation by the least common denominator. [latex-display]\begin{array}{l}6\left(\frac{x}{3}+\frac{y}{6}\right)=6\left(3\right)\hfill \\ \text{ }2x+y=18\hfill \\ 4\left(\frac{x}{2}-\frac{y}{4}\right)=4\left(1\right)\hfill \\ \text{ }2x-y=4\hfill \end{array}[/latex-display] Now multiply the second equation by [latex]-1[/latex] so that we can eliminate the x-variable. [latex-display]\begin{array}{l}-1\left(2x-y\right)=-1\left(4\right)\hfill \\ \text{ }-2x+y=-4\hfill \end{array}[/latex-display] Add the two equations to eliminate the x-variable and solve the resulting equation. [latex-display]\begin{array}\ \hfill 2x+y=18 \\ \hfill−2x+y=−4 \\ \text{_____________} \\ \hfill 2y=14 \\ \hfill y=7 \end{array}[/latex-display] Substitute [latex]y=7[/latex] into the first equation. [latex-display]\begin{array}{l}2x+\left(7\right)=18\hfill \\ \text{ }2x=11\hfill \\ \text{ }x=\frac{11}{2}\hfill \\ \text{ }=7.5\hfill \end{array}[/latex-display] The solution is [latex]\left(\frac{11}{2},7\right)[/latex]. Check it in the other equation. [latex-display]\begin{array}{c}\frac{x}{2}-\frac{y}{4}=1\\ \frac{\frac{11}{2}}{2}-\frac{7}{4}=1\\ \frac{11}{4}-\frac{7}{4}=1\\ \frac{4}{4}=1\end{array}[/latex-display]

Try It

Solve the system of equations by addition. [latex-display]\begin{array}{c}2x+3y=8\\ 3x+5y=10\end{array}[/latex-display]

Answer: [latex]\left(10,-4\right)[/latex]

in the following video we present more examples of how to use the addition (elimination) method to solve a system of two linear equations. https://youtu.be/ova8GSmPV4o

Licenses & Attributions

CC licensed content, Shared previously

  • Solving Systems of Equations using Elimination. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Solving Systems of Equations using Substitution . Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Question ID 115164, 115120, 115110. Authored by: Shabazian, Roy. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.