Reflections
Learning Objectives
- Graph functions using reflections about the [latex]x[/latex] -axis and the [latex]y[/latex] -axis.
- Determine whether a function is even, odd, or neither from its graph.
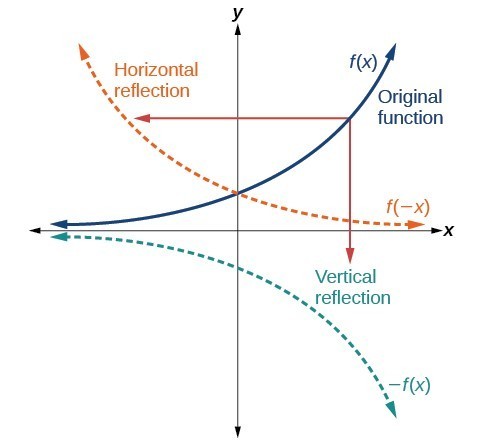 Vertical and horizontal reflections of a function.
Vertical and horizontal reflections of a function.A General Note: Reflections
Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=-f\left(x\right)[/latex] is a vertical reflection of the function [latex]f\left(x\right)[/latex], sometimes called a reflection about (or over, or through) the x-axis. Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=f\left(-x\right)[/latex] is a horizontal reflection of the function [latex]f\left(x\right)[/latex], sometimes called a reflection about the y-axis.How To: Given a function, reflect the graph both vertically and horizontally.
- Multiply all outputs by –1 for a vertical reflection. The new graph is a reflection of the original graph about the x-axis.
- Multiply all inputs by –1 for a horizontal reflection. The new graph is a reflection of the original graph about the y-axis.
Example: Reflecting a Graph Horizontally and Vertically
Reflect the graph of [latex]s\left(t\right)=\sqrt{t}[/latex] (a) vertically and (b) horizontally.Answer: a. Reflecting the graph vertically means that each output value will be reflected over the horizontal t-axis as shown below.
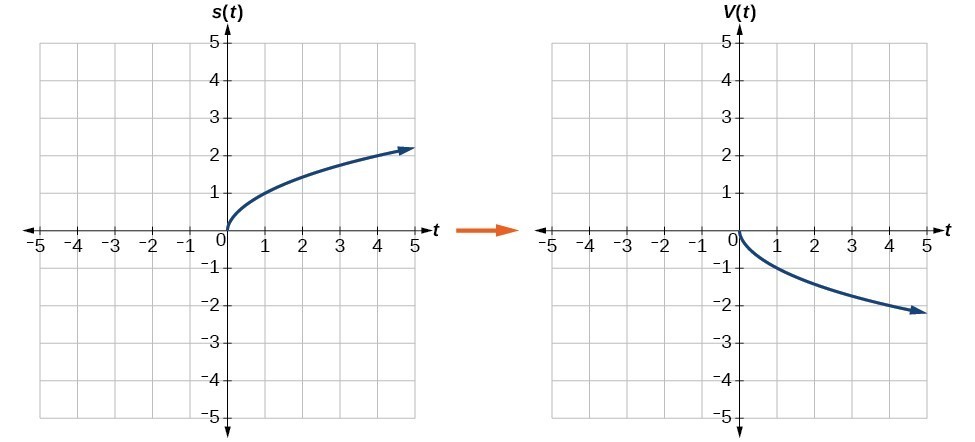 Vertical reflection of the square root function
Vertical reflection of the square root function[latex]V\left(t\right)=-s\left(t\right)\text{ or }V\left(t\right)=-\sqrt{t}[/latex]
Notice that this is an outside change, or vertical shift, that affects the output [latex]s\left(t\right)[/latex] values, so the negative sign belongs outside of the function. b. Reflecting horizontally means that each input value will be reflected over the vertical axis as shown below.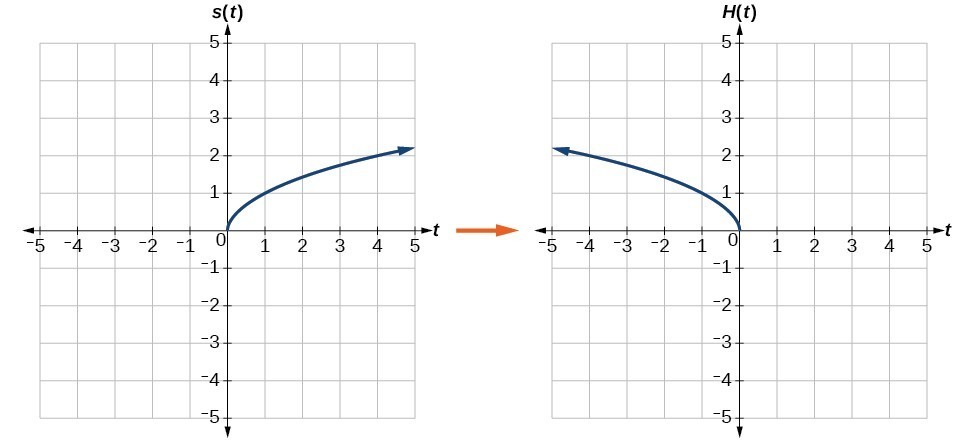 Horizontal reflection of the square root function
Horizontal reflection of the square root function[latex]H\left(t\right)=s\left(-t\right)\text{ or }H\left(t\right)=\sqrt{-t}[/latex]
Notice that this is an inside change or horizontal change that affects the input values, so the negative sign is on the inside of the function. Note that these transformations can affect the domain and range of the functions. While the original square root function has domain [latex]\left[0,\infty \right)[/latex] and range [latex]\left[0,\infty \right)[/latex], the vertical reflection gives the [latex]V\left(t\right)[/latex] function the range [latex]\left(-\infty ,0\right][/latex] and the horizontal reflection gives the [latex]H\left(t\right)[/latex] function the domain [latex]\left(-\infty ,0\right][/latex].Try It
Use Desmos to reflect the graph of [latex]f\left(x\right)=|x - 1|[/latex] (a) vertically and (b) horizontally.Answer:
a)
 b)
b)

Try It
Use Desmos to determine whether the following functions are even, odd, or neither:- [latex]f(x) = \sqrt{x^2-4}[/latex]
- [latex]f(x) = 2x^3-4x[/latex]
- [latex]f(x) = 2x^3+3x^2-4x+5[/latex]
Answer:
- even
- odd
- neither
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 112701, 60650, 113454,112703. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
