Putting It Together: Linear and Absolute Value Functions
At the start of this module, you were wondering whether you could earn a profit by making bikes and were given a profit function.[latex]P\left(x\right)=R\left(x\right)-C\left(x\right)[/latex]
where,
[latex]x[/latex] = the number of bikes produced and sold
[latex]P(x)[/latex] = profit as a function of x
[latex]R(x)[/latex] = revenue as a function of x
[latex]C(x)[/latex] = cost as a function of x
Profit, revenue, and cost are all linear functions. They are a function of the number of bikes sold. Remember that you were planning to sell each bike for $600, and it cost you $1,600 for fixed costs plus $200 per bike. Since you take in $600 for each bike you sell, revenue is[latex]R\left(x\right)=600x[/latex]
Your costs are $200 per bike plus a fixed cost of $1600, so your overall cost is[latex]C\left(x\right)=200x+1600[/latex]
That means that profit becomes[latex]P\left(x\right)=600x-\left(200x+1600\right)[/latex]
[latex]=400x-1600[/latex]
With that in mind, let’s take another look at the table. The profit is found by subtracting the cost function from the revenue function for each number of bikes.| Number of bikes ([latex]x[/latex]) | Profit ($) |
| 2 | [latex]400\left(2\right)-1600=-800[/latex] (loss) |
| 5 | [latex]400\left(5\right)-1600=400[/latex] |
| 10 | [latex]400\left(10\right)-1600=2400[/latex] |
[latex]R\left(x\right)=C\left(x\right)[/latex]
[latex]600x=200x+1600[/latex]
[latex]400x=1600[/latex]
[latex]x=4[/latex]
That means that if you sell 4 bikes, you will take in the same amount you spend to make the bikes. So selling less than 4 bikes will result in a loss and selling more than 4 bikes will result in a profit. Another method for finding the break-even point is by graphing the two functions. You can use whichever method of graphing you find useful. To plot points, for example, make a list of values for each function. Then use them to determine coordinates that you can plot. [latex-display]R\left(x\right)=600x C\left(x\right)=200x+1600[/latex-display]| x | R(x) | x | C(x) | |||
| 0 | 0 | → (0, 0) | 0 | 1600 | → (0, 1600) | |
| 2 | 1200 | → (2, 1200) | 2 | 2000 | → (2, 2000) | |
| 4 | 2400 | → (4, 2400) | 4 | 2400 | → (4, 2400) | |
| 6 | 3600 | → (6, 3600) | 6 | 2800 | → (6, 2800) | |
| 8 | 4800 | → (8, 4800) | 8 | 3200 | → (8, 3200) |
| y-intercept = 0 | y-intercept = 1600 |
| slope = 600 | slope = 200 |
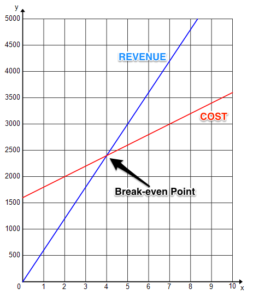Now we can see the breakpoint right away. It is the point at which the cost function intersects the revenue function because they are equal. It occurs when [latex]x=4[/latex]. At this point you neither make a profit nor incur a loss.
The last question to consider is how changing your price affects your profit. If your costs remain the same, increasing the price you charge will shift your break-even point to a lower number of bikes and increase your revenue for every value of [latex]x[/latex]. But people may not buy as many bikes. Lowering your price will shift your break-even point to a higher number of bikes and decrease your revenue for every value of [latex]x[/latex]. However, more people may buy your bikes.
Let’s take a look at the graphs for two other possible prices.
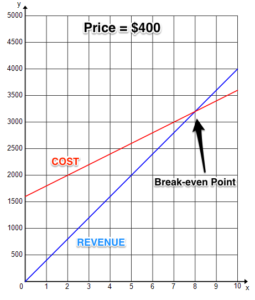
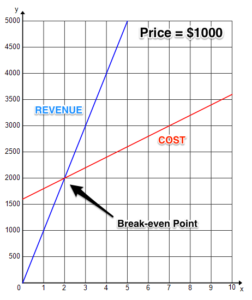Graphing let’s you quickly see a visual representation of the functions and how they are related to one another. See how the break-even point shifts to 8 bikes for a lower price and only 2 bikes for a higher price.
So writing, graphing, and comparing linear functions can be quite useful. As for deciding what price people are willing to pay for your bike, that’s a whole different topic!Licenses & Attributions
CC licensed content, Original
- Putting It Together: Linear and Absolute Value Functions. Authored by: Lumen Learning. License: CC BY: Attribution.
