We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Express and Plot Complex Numbers

Learning Objectives

  • Express square roots of negative numbers as multiples of i
  • Plot complex numbers on the complex plane
We know how to find the square root of any positive real number. In a similar way, we can find the square root of a negative number. The difference is that the root is not real. If the value in the radicand is negative, the root is said to be an imaginary number. The imaginary number [latex]i[/latex] is defined as the square root of negative 1.

[latex]\sqrt{-1}=i[/latex]

So, using properties of radicals,

[latex]{i}^{2}={\left(\sqrt{-1}\right)}^{2}=-1[/latex]

We can write the square root of any negative number as a multiple of i. Consider the square root of –25.

[latex]\begin{array}{l} \sqrt{-25}=\sqrt{25\cdot \left(-1\right)}\hfill \\ \text{ }=\sqrt{25}\sqrt{-1}\hfill \\ \text{ }=5i\hfill \end{array}[/latex]

We use 5i and not [latex]-\text{5}i[/latex] because the principal root of 25 is the positive root.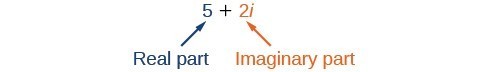 Showing the real and imaginary parts of 5 + 2i. In this complex number, 5 is the real part and 2i is the complex part. A complex number is the sum of a real number and an imaginary number. A complex number is expressed in standard form when written a + bi where a is the real part and bi is the imaginary part. For example, [latex]5+2i[/latex] is a complex number. So, too, is [latex]3+4\sqrt{3}i[/latex]. Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers.

A General Note: Imaginary and Complex Numbers

A complex number is a number of the form [latex]a+bi[/latex] where
  • a is the real part of the complex number.
  • bi is the imaginary part of the complex number.
If [latex]b=0[/latex], then [latex]a+bi[/latex] is a real number. If [latex]a=0[/latex] and b is not equal to 0, the complex number is called an imaginary number. An imaginary number is an even root of a negative number.

How To: Given an imaginary number, express it in standard form.

  1. Write [latex]\sqrt{-a}[/latex] as [latex]\sqrt{a}\sqrt{-1}[/latex].
  2. Express [latex]\sqrt{-1}[/latex] as i.
  3. Write [latex]\sqrt{a}\cdot i[/latex] in simplest form.

Example: Expressing an Imaginary Number in Standard Form

Express [latex]\sqrt{-9}[/latex] in standard form.

Answer: [latex-display]\sqrt{-9}=\sqrt{9}\sqrt{-1}=3i[/latex-display] In standard form, this is [latex]0+3i[/latex].

Try It

Express [latex]\sqrt{-24}[/latex] in standard form.

Answer: [latex]\sqrt{-24}=0+2i\sqrt{6}\\[/latex]

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Introduction to Complex Numbers. Authored by: Sousa, James. License: CC BY: Attribution.
  • Question ID 61706. Authored by: Day, Alyson. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 65709. Authored by: Kaslik,Pete, mb Lippman,David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].