Explicit Formulas for Geometric Sequences
Learning Objectives
- Write a recursive formula given a sequence of numbers
- Given two terms in a geometric sequence, find a third
- Solve an application problem using a geometric sequence
Using Recursive Formulas for Geometric Sequences
A recursive formula allows us to find any term of a geometric sequence by using the previous term. Each term is the product of the common ratio and the previous term. For example, suppose the common ratio is 9. Then each term is nine times the previous term. As with any recursive formula, the initial term must be given.A General Note: Recursive Formula for a Geometric Sequence
The recursive formula for a geometric sequence with common ratio [latex]r[/latex] and first term [latex]{a}_{1}[/latex] is [latex-display]{a}_{n}=r{a}_{n - 1},n\ge 2[/latex-display]How To: Given the first several terms of a geometric sequence, write its recursive formula.
- State the initial term.
- Find the common ratio by dividing any term by the preceding term.
- Substitute the common ratio into the recursive formula for a geometric sequence.
Example: Using Recursive Formulas for Geometric Sequences
Write a recursive formula for the following geometric sequence.[latex]\left\{6\text{, }9\text{, }13.5\text{, }20.25\text{, }...\right\}[/latex]
Answer: The first term is given as 6. The common ratio can be found by dividing the second term by the first term.
[latex]r=\frac{9}{6}=1.5[/latex]
Substitute the common ratio into the recursive formula for geometric sequences and define [latex]{a}_{1}[/latex].[latex]\begin{array}{l}{a}_{n}=r{a}_{n - 1}\\ {a}_{n}=1.5{a}_{n - 1}\text{ for }n\ge 2\\ {a}_{1}=6\end{array}[/latex]
Analysis of the Solution
The sequence of data points follows an exponential pattern. The common ratio is also the base of an exponential function.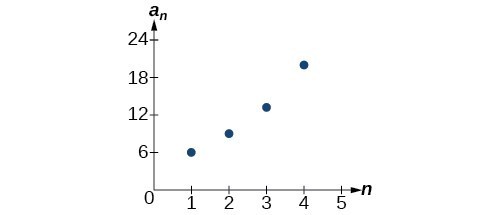
Q & A
Do we have to divide the second term by the first term to find the common ratio?
No. We can divide any term in the sequence by the previous term. It is, however, most common to divide the second term by the first term because it is often the easiest method of finding the common ratio.Try It
Write a recursive formula for the following geometric sequence. [latex-display]\left\{2\text{, }\frac{4}{3}\text{, }\frac{8}{9}\text{, }\frac{16}{27}\text{, }...\right\}[/latex-display]Answer: [latex]\begin{array}{l}{a}_{1}=2\\ {a}_{n}=\frac{2}{3}{a}_{n - 1}\text{ for }n\ge 2\end{array}[/latex]
Using Explicit Formulas for Geometric Sequences
Because a geometric sequence is an exponential function whose domain is the set of positive integers, and the common ratio is the base of the function, we can write explicit formulas that allow us to find particular terms.[latex]{a}_{n}={a}_{1}{r}^{n - 1}[/latex]
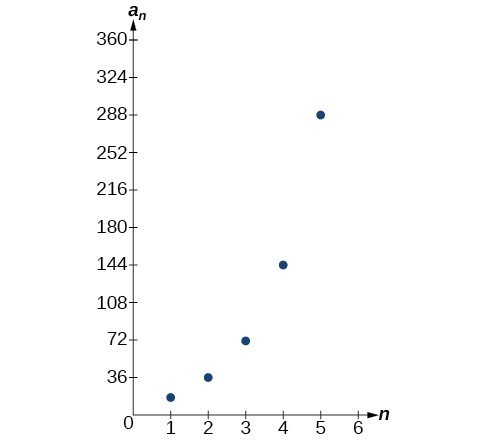
Let’s take a look at the sequence [latex]\left\{18\text{, }36\text{, }72\text{, }144\text{, }288\text{, }...\right\}[/latex]. This is a geometric sequence with a common ratio of 2 and an exponential function with a base of 2. An explicit formula for this sequence is[latex]{a}_{n}=18\cdot {2}^{n - 1}[/latex]
A General Note: Explicit Formula for a Geometric Sequence
The nth term of a geometric sequence is given by the explicit formula:[latex]{a}_{n}={a}_{1}{r}^{n - 1}[/latex]
Example: Writing Terms of Geometric Sequences Using the Explicit Formula
Given a geometric sequence with [latex]{a}_{1}=3[/latex] and [latex]{a}_{4}=24[/latex], find [latex]{a}_{2}[/latex].Answer: The sequence can be written in terms of the initial term and the common ratio [latex]r[/latex].
[latex]3,3r,3{r}^{2},3{r}^{3},..[/latex].
Find the common ratio using the given fourth term.[latex]\begin{array}{ll}{a}_{n}={a}_{1}{r}^{n - 1}\hfill & \hfill \\ {a}_{4}=3{r}^{3}\hfill & \text{Write the fourth term of sequence in terms of }{\alpha }_{1}\text{and }r\hfill \\ 24=3{r}^{3}\hfill & \text{Substitute }24\text{ for}{a}_{4}\hfill \\ 8={r}^{3}\hfill & \text{Divide}\hfill \\ r=2\hfill & \text{Solve for the common ratio}\hfill \end{array}[/latex]
Find the second term by multiplying the first term by the common ratio.[latex]\begin{array}{ll}{a}_{2}\hfill & =2{a}_{1}\hfill \\ \hfill & =2\left(3\right)\hfill \\ \hfill & =6\hfill \end{array}[/latex]
Analysis of the Solution
The common ratio is multiplied by the first term once to find the second term, twice to find the third term, three times to find the fourth term, and so on. The tenth term could be found by multiplying the first term by the common ratio nine times or by multiplying by the common ratio raised to the ninth power.Try It
Given a geometric sequence with [latex]{a}_{2}=4[/latex] and [latex]{a}_{3}=32[/latex] , find [latex]{a}_{6}[/latex].Answer: [latex]{a}_{6}=16,384[/latex]
[latex]{a}_{n}={a}_{0}{r}^{n}[/latex]
Example: Solving Application Problems with Geometric Sequences
In 2013, the number of students in a small school is 284. It is estimated that the student population will increase by 4% each year.- Write a formula for the student population.
- Estimate the student population in 2020.
Answer:
- The situation can be modeled by a geometric sequence with an initial term of 284. The student population will be 104% of the prior year, so the common ratio is 1.04.Let [latex]P[/latex] be the student population and [latex]n[/latex] be the number of years after 2013. Using the explicit formula for a geometric sequence we get [latex]{P}_{n} =284\cdot {1.04}^{n}[/latex]
- We can find the number of years since 2013 by subtracting. [latex-display]2020 - 2013=7[/latex-display] We are looking for the population after 7 years. We can substitute 7 for [latex]n[/latex] to estimate the population in 2020. [latex-display]{P}_{7}=284\cdot {1.04}^{7}\approx 374[/latex-display] The student population will be about 374 in 2020.
Try It
A business starts a new website. Initially the number of hits is 293 due to the curiosity factor. The business estimates the number of hits will increase by 2.6% per week.- Write a formula for the number of hits.
- Estimate the number of hits in 5 weeks.
Answer:
- [latex]{P}_{n} = 293\cdot 1.026{a}^{n}[/latex]
- The number of hits will be about 333.
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Geometric Sequences . Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 29756. Authored by: McClure,Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY +GPL.
- Question ID 5856. Authored by: WebWork-Rochester, mb Lippman,David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
