Equations of Hyperbolas
Learning Objectives
- Derive an equation for a hyperbola centered at the origin
- Write an equation for a hyperbola centered at the origin
- Solve an applied problem involving hyperbolas
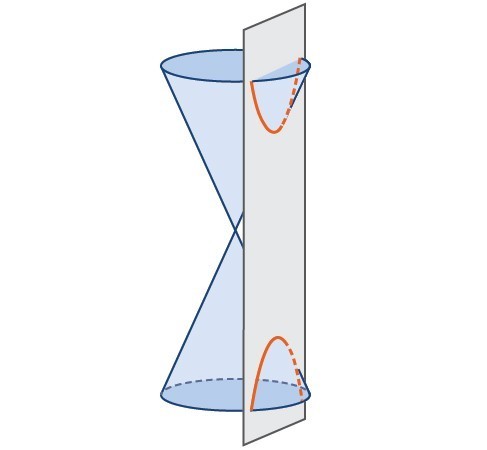 A hyperbola
A hyperbola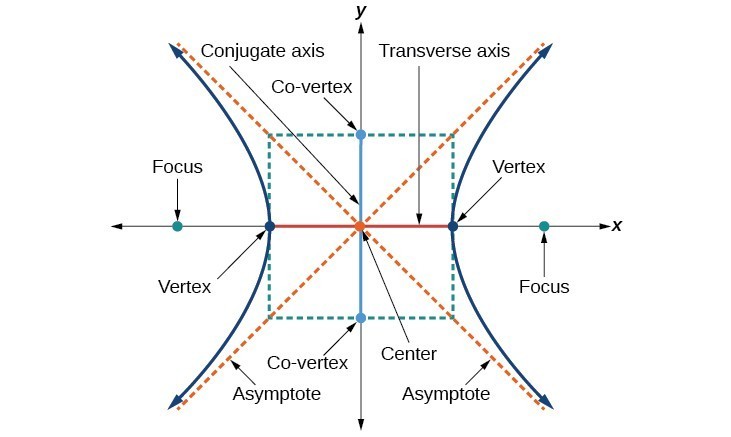 Key features of the hyperbola
Key features of the hyperbolaDeriving the Equation of a Hyperbola Centered at the Origin
Let [latex]\left(-c,0\right)[/latex] and [latex]\left(c,0\right)[/latex] be the foci of a hyperbola centered at the origin. The hyperbola is the set of all points [latex]\left(x,y\right)[/latex] such that the difference of the distances from [latex]\left(x,y\right)[/latex] to the foci is constant.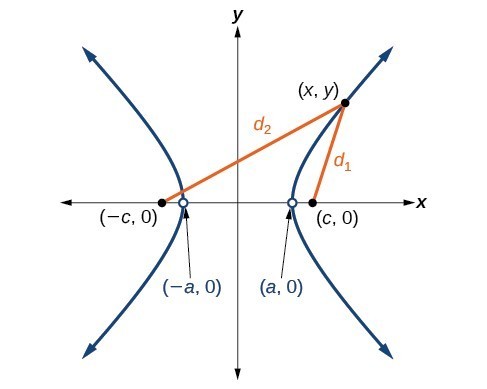 If [latex]\left(a,0\right)[/latex] is a vertex of the hyperbola, the distance from [latex]\left(-c,0\right)[/latex] to [latex]\left(a,0\right)[/latex] is [latex]a-\left(-c\right)=a+c[/latex]. The distance from [latex]\left(c,0\right)[/latex] to [latex]\left(a,0\right)[/latex] is [latex]c-a[/latex]. The sum of the distances from the foci to the vertex is
If [latex]\left(a,0\right)[/latex] is a vertex of the hyperbola, the distance from [latex]\left(-c,0\right)[/latex] to [latex]\left(a,0\right)[/latex] is [latex]a-\left(-c\right)=a+c[/latex]. The distance from [latex]\left(c,0\right)[/latex] to [latex]\left(a,0\right)[/latex] is [latex]c-a[/latex]. The sum of the distances from the foci to the vertex is
[latex]\left(a+c\right)-\left(c-a\right)=2a[/latex]
If [latex]\left(x,y\right)[/latex] is a point on the hyperbola, we can define the following variables:[latex]\begin{array}{l}{d}_{2}=\text{the distance from }\left(-c,0\right)\text{ to }\left(x,y\right)\\ {d}_{1}=\text{the distance from }\left(c,0\right)\text{ to }\left(x,y\right)\end{array}[/latex]
By definition of a hyperbola, [latex]{d}_{2}-{d}_{1}[/latex] is constant for any point [latex]\left(x,y\right)[/latex] on the hyperbola. We know that the difference of these distances is [latex]2a[/latex] for the vertex [latex]\left(a,0\right)[/latex]. It follows that [latex]{d}_{2}-{d}_{1}=2a[/latex] for any point on the hyperbola. As with the derivation of the equation of an ellipse, we will begin by applying the distance formula. The rest of the derivation is algebraic. Compare this derivation with the one from the previous section for ellipses.[latex]\begin{array}{ll}\text{ }{d}_{2}-{d}_{1}=\sqrt{{\left(x-\left(-c\right)\right)}^{2}+{\left(y - 0\right)}^{2}}-\sqrt{{\left(x-c\right)}^{2}+{\left(y - 0\right)}^{2}}=2a\hfill & \text{Distance Formula}\hfill \\ \sqrt{{\left(x+c\right)}^{2}+{y}^{2}}-\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}=2a\hfill & \text{Simplify expressions}\text{.}\hfill \\ \text{ }\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}=2a+\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\hfill & \text{Move radical to opposite side}\text{.}\hfill \\ \text{ }{\left(x+c\right)}^{2}+{y}^{2}={\left(2a+\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\right)}^{2}\hfill & \text{Square both sides}\text{.}\hfill \\ \text{ }{x}^{2}+2cx+{c}^{2}+{y}^{2}=4{a}^{2}+4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}+{\left(x-c\right)}^{2}+{y}^{2}\hfill & \text{Expand the squares}\text{.}\hfill \\ \text{ }{x}^{2}+2cx+{c}^{2}+{y}^{2}=4{a}^{2}+4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}+{x}^{2}-2cx+{c}^{2}+{y}^{2}\hfill & \text{Expand remaining square}\text{.}\hfill \\ \text{ }2cx=4{a}^{2}+4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}-2cx\hfill & \text{Combine like terms}\text{.}\hfill \\ \text{ }4cx - 4{a}^{2}=4a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\hfill & \text{Isolate the radical}\text{.}\hfill \\ \text{ }cx-{a}^{2}=a\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\hfill & \text{Divide by 4}\text{.}\hfill \\ \text{ }{\left(cx-{a}^{2}\right)}^{2}={a}^{2}{\left[\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}\right]}^{2}\hfill & \text{Square both sides}\text{.}\hfill \\ \text{ }{c}^{2}{x}^{2}-2{a}^{2}cx+{a}^{4}={a}^{2}\left({x}^{2}-2cx+{c}^{2}+{y}^{2}\right)\hfill & \text{Expand the squares}\text{.}\hfill \\ \text{ }{c}^{2}{x}^{2}-2{a}^{2}cx+{a}^{4}={a}^{2}{x}^{2}-2{a}^{2}cx+{a}^{2}{c}^{2}+{a}^{2}{y}^{2}\hfill & \text{Distribute }{a}^{2}\text{.}\hfill \\ \text{ }{a}^{4}+{c}^{2}{x}^{2}={a}^{2}{x}^{2}+{a}^{2}{c}^{2}+{a}^{2}{y}^{2}\hfill & \text{Combine like terms}\text{.}\hfill \\ \text{ }{c}^{2}{x}^{2}-{a}^{2}{x}^{2}-{a}^{2}{y}^{2}={a}^{2}{c}^{2}-{a}^{4}\hfill & \text{Rearrange terms}\text{.}\hfill \\ \text{ }{x}^{2}\left({c}^{2}-{a}^{2}\right)-{a}^{2}{y}^{2}={a}^{2}\left({c}^{2}-{a}^{2}\right)\hfill & \text{Factor common terms}\text{.}\hfill \\ \text{ }{x}^{2}{b}^{2}-{a}^{2}{y}^{2}={a}^{2}{b}^{2}\hfill & \text{Set }{b}^{2}={c}^{2}-{a}^{2}.\hfill \\ \text{ }\frac{{x}^{2}{b}^{2}}{{a}^{2}{b}^{2}}-\frac{{a}^{2}{y}^{2}}{{a}^{2}{b}^{2}}=\frac{{a}^{2}{b}^{2}}{{a}^{2}{b}^{2}}\hfill & \text{Divide both sides by }{a}^{2}{b}^{2}\hfill \\ \text{ }\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1\hfill & \hfill \end{array}[/latex]
This equation defines a hyperbola centered at the origin with vertices [latex]\left(\pm a,0\right)[/latex] and co-vertices [latex]\left(0\pm b\right)[/latex].A General Note: Standard Forms of the Equation of a Hyperbola with Center (0,0)
The standard form of the equation of a hyperbola with center [latex]\left(0,0\right)[/latex] and transverse axis on the x-axis is [latex-display]\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1[/latex-display] where- the length of the transverse axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(\pm a,0\right)[/latex]
- the length of the conjugate axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(0,\pm b\right)[/latex]
- the distance between the foci is [latex]2c[/latex], where [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]
- the coordinates of the foci are [latex]\left(\pm c,0\right)[/latex]
- the equations of the asymptotes are [latex]y=\pm \frac{b}{a}x[/latex]
- the length of the transverse axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(0,\pm a\right)[/latex]
- the length of the conjugate axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(\pm b,0\right)[/latex]
- the distance between the foci is [latex]2c[/latex], where [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]
- the coordinates of the foci are [latex]\left(0,\pm c\right)[/latex]
- the equations of the asymptotes are [latex]y=\pm \frac{a}{b}x[/latex]
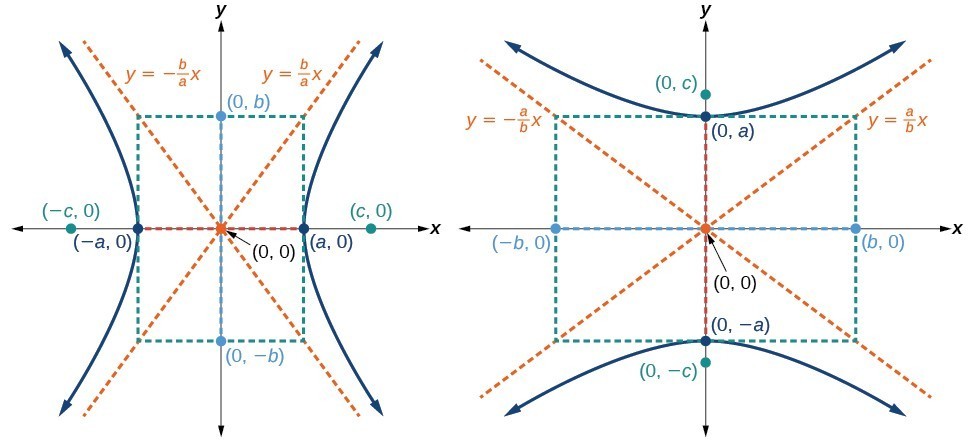 (a) Horizontal hyperbola with center [latex]\left(0,0\right)[/latex] (b) Vertical hyperbola with center [latex]\left(0,0\right)[/latex]
(a) Horizontal hyperbola with center [latex]\left(0,0\right)[/latex] (b) Vertical hyperbola with center [latex]\left(0,0\right)[/latex]How To: Given the equation of a hyperbola in standard form, locate its vertices and foci.
- Determine whether the transverse axis lies on the x- or y-axis. Notice that [latex]{a}^{2}[/latex] is always under the variable with the positive coefficient. So, if you set the other variable equal to zero, you can easily find the intercepts. In the case where the hyperbola is centered at the origin, the intercepts coincide with the vertices.
- Solve for [latex]a[/latex] using the equation [latex]a=\sqrt{{a}^{2}}[/latex].
- Solve for [latex]c[/latex] using the equation [latex]c=\sqrt{{a}^{2}+{b}^{2}}[/latex].
Example: Locating a Hyperbola’s Vertices and Foci
Identify the vertices and foci of the hyperbola with equation [latex]\frac{{y}^{2}}{49}-\frac{{x}^{2}}{32}=1[/latex].Answer: The equation has the form [latex]\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}=1[/latex], so the transverse axis lies on the y-axis. The hyperbola is centered at the origin, so the vertices serve as the y-intercepts of the graph. To find the vertices, set [latex]x=0[/latex], and solve for [latex]y[/latex].
[latex]\begin{array}{l}1=\frac{{y}^{2}}{49}-\frac{{x}^{2}}{32}\hfill \\ 1=\frac{{y}^{2}}{49}-\frac{{0}^{2}}{32}\hfill \\ 1=\frac{{y}^{2}}{49}\hfill \\ {y}^{2}=49\hfill \\ y=\pm \sqrt{49}=\pm 7\hfill \end{array}[/latex]
The foci are located at [latex]\left(0,\pm c\right)[/latex]. Solving for [latex]c[/latex],[latex]c=\sqrt{{a}^{2}+{b}^{2}}=\sqrt{49+32}=\sqrt{81}=9[/latex]
Therefore, the vertices are located at [latex]\left(0,\pm 7\right)[/latex], and the foci are located at [latex]\left(0,9\right)[/latex].Try It
Identify the vertices and foci of the hyperbola with equation [latex]\frac{{x}^{2}}{9}-\frac{{y}^{2}}{25}=1[/latex].Answer: Vertices: [latex]\left(\pm 3,0\right)[/latex]; Foci: [latex]\left(\pm \sqrt{34},0\right)[/latex]
Hyperbolas Not Centered at the Origin
Like the graphs for other equations, the graph of a hyperbola can be translated. If a hyperbola is translated [latex]h[/latex] units horizontally and [latex]k[/latex] units vertically, the center of the hyperbola will be [latex]\left(h,k\right)[/latex]. This translation results in the standard form of the equation we saw previously, with [latex]x[/latex] replaced by [latex]\left(x-h\right)[/latex] and [latex]y[/latex] replaced by [latex]\left(y-k\right)[/latex].A General Note: Standard Forms of the Equation of a Hyperbola with Center (h, k)
The standard form of the equation of a hyperbola with center [latex]\left(h,k\right)[/latex] and transverse axis parallel to the x-axis is [latex-display]\frac{{\left(x-h\right)}^{2}}{{a}^{2}}-\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex-display] where- the length of the transverse axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(h\pm a,k\right)[/latex]
- the length of the conjugate axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(h,k\pm b\right)[/latex]
- the distance between the foci is [latex]2c[/latex], where [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]
- the coordinates of the foci are [latex]\left(h\pm c,k\right)[/latex]
- the length of the transverse axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(h,k\pm a\right)[/latex]
- the length of the conjugate axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(h\pm b,k\right)[/latex]
- the distance between the foci is [latex]2c[/latex], where [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]
- the coordinates of the foci are [latex]\left(h,k\pm c\right)[/latex]
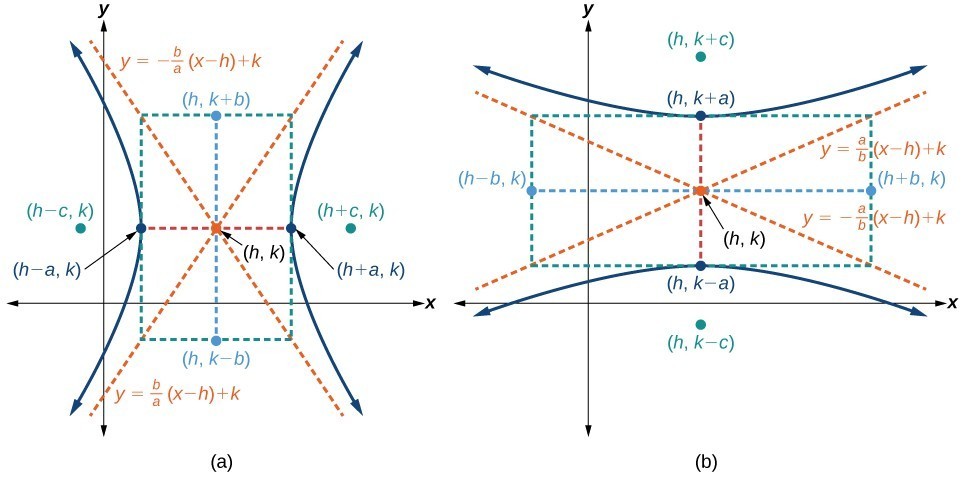 (a) Horizontal hyperbola with center [latex]\left(h,k\right)[/latex] (b) Vertical hyperbola with center [latex]\left(h,k\right)[/latex]
(a) Horizontal hyperbola with center [latex]\left(h,k\right)[/latex] (b) Vertical hyperbola with center [latex]\left(h,k\right)[/latex]How To: Given the vertices and foci of a hyperbola centered at [latex]\left(h,k\right)[/latex], write its equation in standard form.
- Determine whether the transverse axis is parallel to the x- or y-axis.
- If the y-coordinates of the given vertices and foci are the same, then the transverse axis is parallel to the x-axis. Use the standard form [latex]\frac{{\left(x-h\right)}^{2}}{{a}^{2}}-\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex].
- If the x-coordinates of the given vertices and foci are the same, then the transverse axis is parallel to the y-axis. Use the standard form [latex]\frac{{\left(y-k\right)}^{2}}{{a}^{2}}-\frac{{\left(x-h\right)}^{2}}{{b}^{2}}=1[/latex].
- Identify the center of the hyperbola, [latex]\left(h,k\right)[/latex], using the midpoint formula and the given coordinates for the vertices.
- Find [latex]{a}^{2}[/latex] by solving for the length of the transverse axis, [latex]2a[/latex] , which is the distance between the given vertices.
- Find [latex]{c}^{2}[/latex] using [latex]h[/latex] and [latex]k[/latex] found in Step 2 along with the given coordinates for the foci.
- Solve for [latex]{b}^{2}[/latex] using the equation [latex]{b}^{2}={c}^{2}-{a}^{2}[/latex].
- Substitute the values for [latex]h,k,{a}^{2}[/latex], and [latex]{b}^{2}[/latex] into the standard form of the equation determined in Step 1.
Example: Finding the Equation of a Hyperbola Centered at (h, k) Given its Foci and Vertices
What is the standard form equation of the hyperbola that has vertices at [latex]\left(0,-2\right)[/latex] and [latex]\left(6,-2\right)[/latex] and foci at [latex]\left(-2,-2\right)[/latex] and [latex]\left(8,-2\right)?[/latex]Answer: The y-coordinates of the vertices and foci are the same, so the transverse axis is parallel to the x-axis. Thus, the equation of the hyperbola will have the form
[latex]\frac{{\left(x-h\right)}^{2}}{{a}^{2}}-\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex]
First, we identify the center, [latex]\left(h,k\right)[/latex]. The center is halfway between the vertices [latex]\left(0,-2\right)[/latex] and [latex]\left(6,-2\right)[/latex]. Applying the midpoint formula, we have[latex]\left(h,k\right)=\left(\frac{0+6}{2},\frac{-2+\left(-2\right)}{2}\right)=\left(3,-2\right)[/latex]
Next, we find [latex]{a}^{2}[/latex]. The length of the transverse axis, [latex]2a[/latex], is bounded by the vertices. So, we can find [latex]{a}^{2}[/latex] by finding the distance between the x-coordinates of the vertices.[latex]\begin{array}{l}2a=|0 - 6|\hfill \\ 2a=6\hfill \\ \text{ }a=3\hfill \\ {a}^{2}=9\hfill \end{array}[/latex]
Now we need to find [latex]{c}^{2}[/latex]. The coordinates of the foci are [latex]\left(h\pm c,k\right)[/latex]. So [latex]\left(h-c,k\right)=\left(-2,-2\right)[/latex] and [latex]\left(h+c,k\right)=\left(8,-2\right)[/latex]. We can use the x-coordinate from either of these points to solve for [latex]c[/latex]. Using the point [latex]\left(8,-2\right)[/latex], and substituting [latex]h=3[/latex],[latex]\begin{array}{l}h+c=8\hfill \\ 3+c=8\hfill \\ \text{ }c=5\hfill \\ \text{ }{c}^{2}=25\hfill \end{array}[/latex]
Next, solve for [latex]{b}^{2}[/latex] using the equation [latex]{b}^{2}={c}^{2}-{a}^{2}:[/latex][latex]\begin{array}{l}{b}^{2}={c}^{2}-{a}^{2}\hfill \\ \text{ }=25 - 9\hfill \\ \text{ }=16\hfill \end{array}[/latex]
Finally, substitute the values found for [latex]h,k,{a}^{2}[/latex], and [latex]{b}^{2}[/latex] into the standard form of the equation.[latex]\frac{{\left(x - 3\right)}^{2}}{9}-\frac{{\left(y+2\right)}^{2}}{16}=1[/latex]
Try It
What is the standard form equation of the hyperbola that has vertices [latex]\left(1,-2\right)[/latex] and [latex]\left(1,\text{8}\right)[/latex] and foci [latex]\left(1,-10\right)[/latex] and [latex]\left(1,16\right)?[/latex]Answer: [latex]\frac{{\left(y - 3\right)}^{2}}{25}+\frac{{\left(x - 1\right)}^{2}}{144}=1[/latex]
Solving Applied Problems Involving Hyperbolas
As we discussed at the beginning of this section, hyperbolas have real-world applications in many fields, such as astronomy, physics, engineering, and architecture. The design efficiency of hyperbolic cooling towers is particularly interesting. Cooling towers are used to transfer waste heat to the atmosphere and are often touted for their ability to generate power efficiently. Because of their hyperbolic form, these structures are able to withstand extreme winds while requiring less material than any other forms of their size and strength. For example, a 500-foot tower can be made of a reinforced concrete shell only 6 or 8 inches wide! Cooling towers at the Drax power station in North Yorkshire, United Kingdom (credit: Les Haines, Flickr)
Cooling towers at the Drax power station in North Yorkshire, United Kingdom (credit: Les Haines, Flickr)Example: Solving Applied Problems Involving Hyperbolas
The design layout of a cooling tower is shown below. The tower stands 179.6 meters tall. The diameter of the top is 72 meters. At their closest, the sides of the tower are 60 meters apart.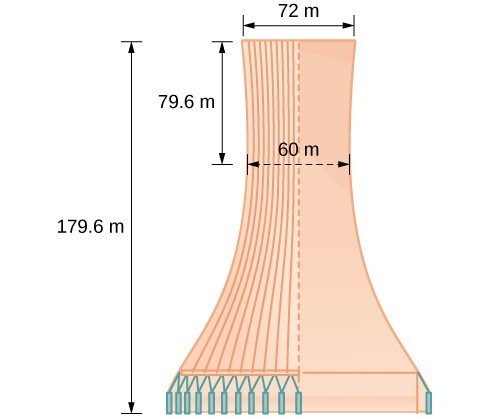 Project design for a natural draft cooling tower
Project design for a natural draft cooling towerAnswer: We are assuming the center of the tower is at the origin, so we can use the standard form of a horizontal hyperbola centered at the origin: [latex]\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1[/latex], where the branches of the hyperbola form the sides of the cooling tower. We must find the values of [latex]{a}^{2}[/latex] and [latex]{b}^{2}[/latex] to complete the model. First, we find [latex]{a}^{2}[/latex]. Recall that the length of the transverse axis of a hyperbola is [latex]2a[/latex]. This length is represented by the distance where the sides are closest, which is given as [latex]\text{ }65.3\text{ }[/latex] meters. So, [latex]2a=60[/latex]. Therefore, [latex]a=30[/latex] and [latex]{a}^{2}=900[/latex]. To solve for [latex]{b}^{2}[/latex], we need to substitute for [latex]x[/latex] and [latex]y[/latex] in our equation using a known point. To do this, we can use the dimensions of the tower to find some point [latex]\left(x,y\right)[/latex] that lies on the hyperbola. We will use the top right corner of the tower to represent that point. Since the y-axis bisects the tower, our x-value can be represented by the radius of the top, or 36 meters. The y-value is represented by the distance from the origin to the top, which is given as 79.6 meters. Therefore,
[latex]\begin{array}{ll}\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1\hfill & \begin{array}{cccc}& & & \end{array}\text{Standard form of horizontal hyperbola}.\hfill \\ \text{ }{b}^{2}=\frac{{y}^{2}}{\frac{{x}^{2}}{{a}^{2}}-1}\hfill & \begin{array}{cccc}& & & \end{array}\text{Isolate }{b}^{2}\hfill \\ \text{ }=\frac{{\left(79.6\right)}^{2}}{\frac{{\left(36\right)}^{2}}{900}-1}\hfill & \begin{array}{cccc}& & & \end{array}\text{Substitute for }{a}^{2},x,\text{ and }y\hfill \\ \text{ }\approx 14400.3636\hfill & \begin{array}{cccc}& & & \end{array}\text{Round to four decimal places}\hfill \end{array}[/latex]
The sides of the tower can be modeled by the hyperbolic equation[latex]\frac{{x}^{2}}{900}-\frac{{y}^{2}}{14400.3636 }=1,\text{or}\frac{{x}^{2}}{{30}^{2}}-\frac{{y}^{2}}{{120.0015}^{2} }=1[/latex]
Try It
A design for a cooling tower project is shown below. Find the equation of the hyperbola that models the sides of the cooling tower. Assume that the center of the hyperbola—indicated by the intersection of dashed perpendicular lines in the figure—is the origin of the coordinate plane. Round final values to four decimal places.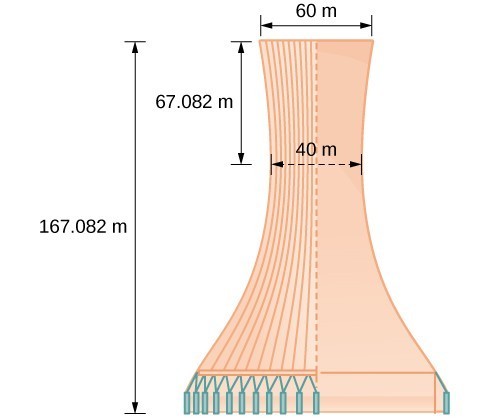
Answer: The sides of the tower can be modeled by the hyperbolic equation. [latex]\frac{{x}^{2}}{400}-\frac{{y}^{2}}{3600}=1\text{or }\frac{{x}^{2}}{{20}^{2}}-\frac{{y}^{2}}{{60}^{2}}=1[/latex].
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 1669. Authored by: WebWork-Rochester, mb Sousa,James. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 70367. Authored by: Shahbazian,Roy. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
