Define and Graph an Inverse
Learning Objectives
- Find and evaluate the inverse of a function in tabular form
- Find and evaluate the inverse of a function given as an equation
- Graph a function's inverse
Inverting Tabular Functions
Suppose we want to find the inverse of a function represented in table form. Remember that the domain of a function is the range of the inverse and the range of the function is the domain of the inverse. So we need to interchange the domain and range. Each row (or column) of inputs becomes the row (or column) of outputs for the inverse function. Similarly, each row (or column) of outputs becomes the row (or column) of inputs for the inverse function.Example: Interpreting the Inverse of a Tabular Function
A function [latex]f\left(t\right)[/latex] is given below, showing distance in miles that a car has traveled in [latex]t[/latex] minutes. Find and interpret [latex]{f}^{-1}\left(70\right)[/latex].| [latex]t\text{ (minutes)}[/latex] | 30 | 50 | 70 | 90 |
| [latex]f\left(t\right)\text{ (miles)}[/latex] | 20 | 40 | 60 | 70 |
Answer: The inverse function takes an output of [latex]f[/latex] and returns an input for [latex]f[/latex]. So in the expression [latex]{f}^{-1}\left(70\right)[/latex], 70 is an output value of the original function, representing 70 miles. The inverse will return the corresponding input of the original function [latex]f[/latex], 90 minutes, so [latex]{f}^{-1}\left(70\right)=90[/latex]. The interpretation of this is that, to drive 70 miles, it took 90 minutes. Alternatively, recall that the definition of the inverse was that if [latex]f\left(a\right)=b[/latex], then [latex]{f}^{-1}\left(b\right)=a[/latex]. By this definition, if we are given [latex]{f}^{-1}\left(70\right)=a[/latex], then we are looking for a value [latex]a[/latex] so that [latex]f\left(a\right)=70[/latex]. In this case, we are looking for a [latex]t[/latex] so that [latex]f\left(t\right)=70[/latex], which is when [latex]t=90[/latex].
Try It
Using the table below, find and interpret (a) [latex]\text{ }f\left(60\right)[/latex], and (b) [latex]\text{ }{f}^{-1}\left(60\right)[/latex].| [latex]t\text{ (minutes)}[/latex] | 30 | 50 | 60 | 70 | 90 |
| [latex]f\left(t\right)\text{ (miles)}[/latex] | 20 | 40 | 50 | 60 | 70 |
Answer: a. [latex]f\left(60\right)=50[/latex]. In 60 minutes, 50 miles are traveled. b. [latex]{f}^{-1}\left(60\right)=70[/latex]. To travel 60 miles, it will take 70 minutes.
Evaluating the Inverse of a Function, Given a Graph of the Original Function
The domain of a function can be read by observing the horizontal extent of its graph. We find the domain of the inverse function by observing the vertical extent of the graph of the original function, because this corresponds to the horizontal extent of the inverse function. Similarly, we find the range of the inverse function by observing the horizontal extent of the graph of the original function, as this is the vertical extent of the inverse function. If we want to evaluate an inverse function, we find its input within its domain, which is all or part of the vertical axis of the original function’s graph.How To: Given the graph of a function, evaluate its inverse at specific points.
- Find the desired input on the y-axis of the given graph.
- Read the inverse function’s output from the x-axis of the given graph.
Example: Evaluating a Function and Its Inverse from a Graph at Specific Points
A function [latex]g\left(x\right)[/latex] is given below. Find [latex]g\left(3\right)[/latex] and [latex]{g}^{-1}\left(3\right)[/latex].
Answer:
To evaluate [latex]g\left(3\right)[/latex], we find 3 on the x-axis and find the corresponding output value on the y-axis. The point [latex]\left(3,1\right)[/latex] tells us that [latex]g\left(3\right)=1[/latex].
To evaluate [latex]{g}^{-1}\left(3\right)[/latex], recall that by definition [latex]{g}^{-1}\left(3\right)[/latex] means the value of x for which [latex]g\left(x\right)=3[/latex]. By looking for the output value 3 on the vertical axis, we find the point [latex]\left(5,3\right)[/latex] on the graph, which means [latex]g\left(5\right)=3[/latex], so by definition, [latex]{g}^{-1}\left(3\right)=5[/latex].

Try It
Using the graph in the previous example, (a) find [latex]{g}^{-1}\left(1\right)[/latex], and (b) estimate [latex]{g}^{-1}\left(4\right)[/latex].Answer: a. 3; b. 5.6
Finding Inverses of Functions Represented by Formulas
Sometimes we will need to know an inverse function for all elements of its domain, not just a few. If the original function is given as a formula—for example, [latex]y[/latex] as a function of [latex]x-[/latex] we can often find the inverse function by solving to obtain [latex]x[/latex] as a function of [latex]y[/latex].How To: Given a function represented by a formula, find the inverse.
- Make sure [latex]f[/latex] is a one-to-one function.
- Solve for [latex]x[/latex].
- Interchange [latex]x[/latex] and [latex]y[/latex].
Example: Inverting the Fahrenheit-to-Celsius Function
Find a formula for the inverse function that gives Fahrenheit temperature as a function of Celsius temperature.[latex]C=\frac{5}{9}\left(F - 32\right)[/latex]
Answer:
[latex]\begin{array}{c}\hfill{ C }=\frac{5}{9}\left(F - 32\right)\hfill \\ C\cdot \frac{9}{5}=F - 32\hfill \\ F=\frac{9}{5}C+32\hfill \end{array}[/latex]
By solving in general, we have uncovered the inverse function. If[latex]C=h\left(F\right)=\frac{5}{9}\left(F - 32\right)[/latex],
then[latex]F={h}^{-1}\left(C\right)=\frac{9}{5}C+32[/latex].
In this case, we introduced a function [latex]h[/latex] to represent the conversion because the input and output variables are descriptive, and writing [latex]{C}^{-1}[/latex] could get confusing.Try It
Solve for [latex]x[/latex] in terms of [latex]y[/latex] given [latex]y=\frac{1}{3}\left(x - 5\right)[/latex]Answer: [latex-display]x=3y+5[/latex-display]
Example: Solving to Find an Inverse Function
Find the inverse of the function [latex]f\left(x\right)=\frac{2}{x - 3}+4[/latex].Answer: [latex-display]\begin{array}{l}y=\frac{2}{x - 3}+4\hfill & \text{Set up an equation}.\hfill \\ y - 4=\frac{2}{x - 3}\hfill & \text{Subtract 4 from both sides}.\hfill \\ x - 3=\frac{2}{y - 4}\hfill & \text{Multiply both sides by }x - 3\text{ and divide by }y - 4.\hfill \\ x=\frac{2}{y - 4}+3\hfill & \text{Add 3 to both sides}.\hfill \end{array}[/latex-display] So [latex]{f}^{-1}\left(y\right)=\frac{2}{y - 4}+3[/latex] or [latex]{f}^{-1}\left(x\right)=\frac{2}{x - 4}+3[/latex].
Analysis of the Solution
The domain and range of [latex]f[/latex] exclude the values 3 and 4, respectively. [latex]f[/latex] and [latex]{f}^{-1}[/latex] are equal at two points but are not the same function, as we can see by creating the table below.| [latex]x[/latex] | 1 | 2 | 5 | [latex]{f}^{-1}\left(y\right)[/latex] |
| [latex]f\left(x\right)[/latex] | 3 | 2 | 5 | [latex]y[/latex] |
Example: Solving to Find an Inverse with Radicals
Find the inverse of the function [latex]f\left(x\right)=2+\sqrt{x - 4}[/latex].Answer: [latex-display]\begin{array}{l}y=2+\sqrt{x - 4}\hfill \\ {\left(y - 2\right)}^{2}=x - 4\hfill \\ x={\left(y - 2\right)}^{2}+4\hfill \end{array}[/latex-display] So [latex]{f}^{-1}\left(x\right)={\left(x - 2\right)}^{2}+4[/latex]. The domain of [latex]f[/latex] is [latex]\left[4,\infty \right)[/latex]. Notice that the range of [latex]f[/latex] is [latex]\left[2,\infty \right)[/latex], so this means that the domain of the inverse function [latex]{f}^{-1}[/latex] is also [latex]\left[2,\infty \right)[/latex].
Analysis of the Solution
The formula we found for [latex]{f}^{-1}\left(x\right)[/latex] looks like it would be valid for all real [latex]x[/latex]. However, [latex]{f}^{-1}[/latex] itself must have an inverse (namely, [latex]f[/latex] ) so we have to restrict the domain of [latex]{f}^{-1}[/latex] to [latex]\left[2,\infty \right)[/latex] in order to make [latex]{f}^{-1}[/latex] a one-to-one function. This domain of [latex]{f}^{-1}[/latex] is exactly the range of [latex]f[/latex].Try It
What is the inverse of the function [latex]f\left(x\right)=2-\sqrt{x}[/latex]? State the domains of both the function and the inverse function. Use Desmos to graph the function, it's inverse, and [latex]f(x) = x[/latex] to check whether you are correct.Answer: [latex]{f}^{-1}\left(x\right)={\left(2-x\right)}^{2};\text{domain}\text{ of} f:\left[0,\infty \right);\text{domain}\text{ of}{ f}^{-1}:\left(-\infty ,2\right]\\[/latex]
Graph a Function's Inverse
Now that we can find the inverse of a function, we will explore the graphs of functions and their inverses. Let us return to the quadratic function [latex]f\left(x\right)={x}^{2}[/latex] restricted to the domain [latex]\left[0,\infty \right)[/latex], on which this function is one-to-one, and graph it as below.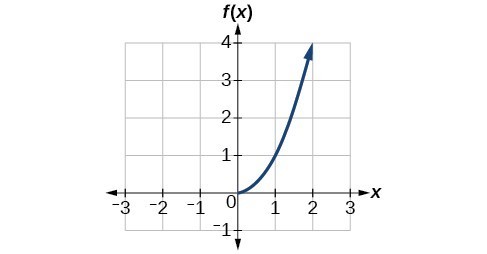 Quadratic function with domain restricted to [0, ∞).
Quadratic function with domain restricted to [0, ∞).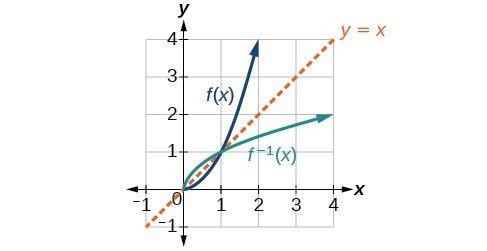 Square and square-root functions on the non-negative domain
Square and square-root functions on the non-negative domainExample: Finding the Inverse of a Function Using Reflection about the Identity Line
Given the graph of [latex]f\left(x\right)[/latex], sketch a graph of [latex]{f}^{-1}\left(x\right)[/latex].
Answer: This is a one-to-one function, so we will be able to sketch an inverse. Note that the graph shown has an apparent domain of [latex]\left(0,\infty \right)[/latex] and range of [latex]\left(-\infty ,\infty \right)[/latex], so the inverse will have a domain of [latex]\left(-\infty ,\infty \right)[/latex] and range of [latex]\left(0,\infty \right)[/latex]. If we reflect this graph over the line [latex]y=x[/latex], the point [latex]\left(1,0\right)[/latex] reflects to [latex]\left(0,1\right)[/latex] and the point [latex]\left(4,2\right)[/latex] reflects to [latex]\left(2,4\right)[/latex]. Sketching the inverse on the same axes as the original graph gives us the result in the graph below.
 The function and its inverse, showing reflection about the identity line
The function and its inverse, showing reflection about the identity line[latex]\frac{1}{\frac{1}{x}}=x[/latex]
Any function [latex]f\left(x\right)=c-x[/latex], where [latex]c[/latex] is a constant, is also equal to its own inverse.Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
