Complex Roots
Learning Objectives
- Find the complex roots of a quadratic function using the quadratic formula
- Use the discriminant to determine whether a quadratic function has real or complex roots
Complex Roots
Now you will hopefully begin to understand why we introduced complex numbers at the beginning of this module. Consider the following function: [latex]f(x)=x^2+2x+3[/latex], and it's graph below: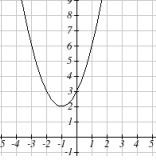 Does this function have roots? It's probably obvious that this function does not cross the x-axis, therefore it doesn't have any x-intercepts. Recall that the x-intercepts of a function are found by setting the function equal to zero:
Does this function have roots? It's probably obvious that this function does not cross the x-axis, therefore it doesn't have any x-intercepts. Recall that the x-intercepts of a function are found by setting the function equal to zero:
[latex]x^2+2x+3=0[/latex]
In the next example, we will solve this equation. You will see that there are roots, but they are not x-intercepts because the function does not contain (x,y) pairs that are on the x-axis. We call these complex roots. By setting the function equal to zero and using the quadratic formula to solve, you will see that the roots contain complex numbers:[latex]x^2+2x+3=0[/latex]
Example
Find the x-intercepts of the quadratic function. [latex]f(x)=x^2+2x+3[/latex]Answer: The x-intercepts of the function [latex]f(x)=x^2+2x+3[/latex] are found by setting it equal to zero, and solving for x since the y values of the x-intercepts are zero. First, identify a, b, c.
[latex]\begin{array}{ccc}x^2+2x+3=0\\a=1,b=2,c=3\end{array}[/latex]
Substitute these values into the quadratic formula.[latex]\begin{array}{c}x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}\\=\frac{-2\pm \sqrt{{2}^{2}-4(1)(3)}}{2(1)}\\=\frac{-2\pm \sqrt{4-12}}{2} \\=\frac{-2\pm \sqrt{-8}}{2}\\\frac{-2\pm 2i\sqrt{2}}{2} \\-1\pm i\sqrt{2}=-1+\sqrt{2},-1-\sqrt{2}\end{array}[/latex]
The solutions to this equations are complex, therefore there are no x-intercepts for the function [latex]f(x)=x^2+2x+3[/latex] in the set of real numbers that can be plotted on the Cartesian Coordinate plane. The graph of the function is plotted on the Cartesian Coordinate plane below: Graph of quadratic function with no x-intercepts in the real numbers.
Graph of quadratic function with no x-intercepts in the real numbers.The Discriminant
The quadratic formula not only generates the solutions to a quadratic equation, it tells us about the nature of the solutions. When we consider the discriminant, or the expression under the radical, [latex]{b}^{2}-4ac[/latex], it tells us whether the solutions are real numbers or complex numbers, and how many solutions of each type to expect. In turn, we can then determine whether a quadratic function has real or complex roots. The table below relates the value of the discriminant to the solutions of a quadratic equation.| Value of Discriminant | Results |
|---|---|
| [latex]{b}^{2}-4ac=0[/latex] | One repeated rational solution |
| [latex]{b}^{2}-4ac>0[/latex], perfect square | Two rational solutions |
| [latex]{b}^{2}-4ac>0[/latex], not a perfect square | Two irrational solutions |
| [latex]{b}^{2}-4ac<0[/latex] | Two complex solutions |
A General Note: The Discriminant
For [latex]a{x}^{2}+bx+c=0[/latex], where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers, the discriminant is the expression under the radical in the quadratic formula: [latex]{b}^{2}-4ac[/latex]. It tells us whether the solutions are real numbers or complex numbers and how many solutions of each type to expect.Example
Use the discriminant to find the nature of the solutions to the following quadratic equations:- [latex]{x}^{2}+4x+4=0[/latex]
- [latex]8{x}^{2}+14x+3=0[/latex]
- [latex]3{x}^{2}-5x - 2=0[/latex]
- [latex]3{x}^{2}-10x+15=0[/latex]
Answer: Calculate the discriminant [latex]{b}^{2}-4ac[/latex] for each equation and state the expected type of solutions.
- [latex]{x}^{2}+4x+4=0[/latex][latex]{b}^{2}-4ac={\left(4\right)}^{2}-4\left(1\right)\left(4\right)=0[/latex]. There will be one repeated rational solution.
- [latex]8{x}^{2}+14x+3=0[/latex][latex]{b}^{2}-4ac={\left(14\right)}^{2}-4\left(8\right)\left(3\right)=100[/latex]. As [latex]100[/latex] is a perfect square, there will be two rational solutions.
- [latex]3{x}^{2}-5x - 2=0[/latex][latex]{b}^{2}-4ac={\left(-5\right)}^{2}-4\left(3\right)\left(-2\right)=49[/latex]. As [latex]49[/latex] is a perfect square, there will be two rational solutions.
- [latex]3{x}^{2}-10x+15=0[/latex][latex]{b}^{2}-4ac={\left(-10\right)}^{2}-4\left(3\right)\left(15\right)=-80[/latex]. There will be two complex solutions.
- If [latex]b^{2}-4ac>0[/latex], then the number underneath the radical will be a positive value. You can always find the square root of a positive, so evaluating the Quadratic Formula will result in two real solutions (one by adding the positive square root, and one by subtracting it).
- If [latex]b^{2}-4ac=0[/latex], then you will be taking the square root of 0, which is 0. Since adding and subtracting 0 both give the same result, the "[latex]\pm[/late]" portion of the formula doesn't matter. There will be one real repeated solution.
- If [latex]b^{2}-4ac<0[/latex], then the number underneath the radical will be a negative value. Since you cannot find the square root of a negative number using real numbers, there are no real solutions. However, you can use imaginary numbers. You will then have two complex solutions, one by adding the imaginary square root and one by subtracting it.
Example
Use the discriminant to determine how many and what kind of solutions the quadratic equation [latex]x^{2}-4x+10=0[/latex] has.Answer: Evaluate [latex]b^{2}-4ac[/latex]. First note that [latex]a=1,b=−4[/latex], and [latex]c=10[/latex].
[latex]\begin{array}{c}b^{2}-4ac\\\left(-4\right)^{2}-4\left(1\right)\left(10\right)\end{array}[/latex]
The result is a negative number. The discriminant is negative, so the quadratic equation has two complex solutions.[latex]16–40=−24[/latex]
Answer
The quadratic equation [latex]x^{2}-4x+10=0[/latex] has two complex solutions.Licenses & Attributions
CC licensed content, Original
- Question ID 121401. Provided by: Lumen Learning License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Question ID 35145. Authored by: Smart,Jim. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
