We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Behaviors of Functions

Learning Objectives

  • Determine where a function is increasing, decreasing, or constant
  • Find local extrema of a function from a graph
  • Describe behavior of the toolkit functions
As part of exploring how functions change, we can identify intervals over which the function is changing in specific ways. We say that a function is increasing on an interval if the function values increase as the input values increase within that interval. Similarly, a function is decreasing on an interval if the function values decrease as the input values increase over that interval. The average rate of change of an increasing function is positive, and the average rate of change of a decreasing function is negative. The graph below shows examples of increasing and decreasing intervals on a function.
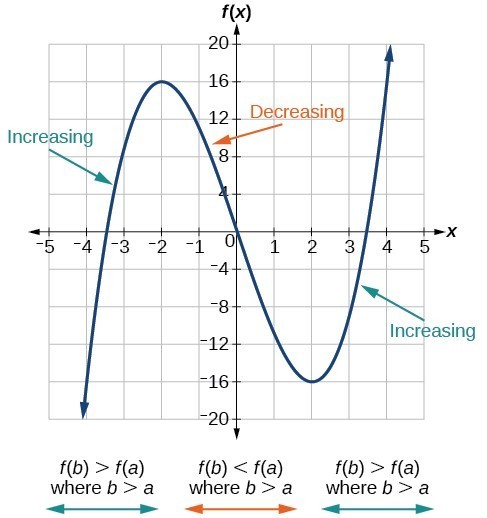Graph of a polynomial that shows the increasing and decreasing intervals and local maximum and minimum. The function [latex]f\left(x\right)={x}^{3}-12x[/latex] is increasing on [latex]\left(-\infty \text{,}-\text{2}\right){{\cup }^{\text{ }}}^{\text{ }}\left(2,\infty \right)[/latex] and is decreasing on [latex]\left(-2\text{,}2\right)[/latex].
This video further explains how to find where a function is increasing or decreasing. https://www.youtube.com/watch?v=78b4HOMVcKM While some functions are increasing (or decreasing) over their entire domain, many others are not. A value of the input where a function changes from increasing to decreasing (as we go from left to right, that is, as the input variable increases) is called a local maximum. If a function has more than one, we say it has local maxima. Similarly, a value of the input where a function changes from decreasing to increasing as the input variable increases is called a local minimum. The plural form is "local minima." Together, local maxima and minima are called local extrema, or local extreme values, of the function. (The singular form is "extremum.") Often, the term local is replaced by the term relative. In this text, we will use the term local. A function is neither increasing nor decreasing on an interval where it is constant. A function is also neither increasing nor decreasing at extrema. Note that we have to speak of local extrema, because any given local extremum as defined here is not necessarily the highest maximum or lowest minimum in the function’s entire domain. For the function below, the local maximum is 16, and it occurs at [latex]x=-2[/latex]. The local minimum is [latex]-16[/latex] and it occurs at [latex]x=2[/latex]. 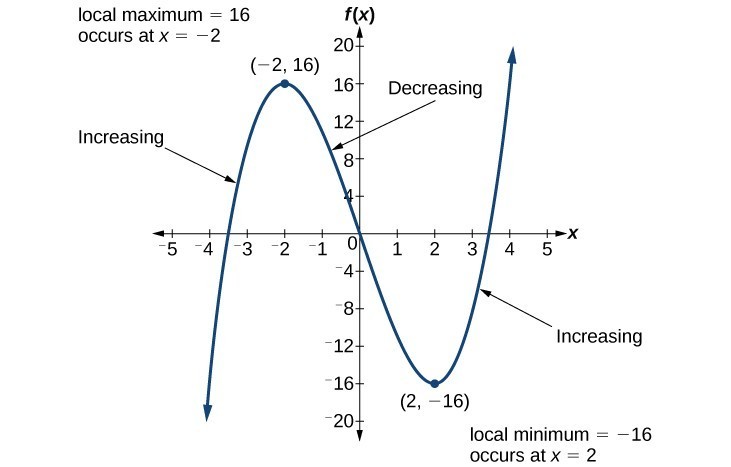Graph of a polynomial that shows the increasing and decreasing intervals and local maximum and minimum. The local maximum is 16 and occurs at x = negative 2. This is the point negative 2, 16. The local minimum is negative 16 and occurs at x = 2. This is the point 2, negative 16. To locate the local maxima and minima from a graph, we need to observe the graph to determine where the graph attains its highest and lowest points, respectively, within an open interval. Like the summit of a roller coaster, the graph of a function is higher at a local maximum than at nearby points on both sides. The graph will also be lower at a local minimum than at neighboring points. The graph below illustrates these ideas for a local maximum.
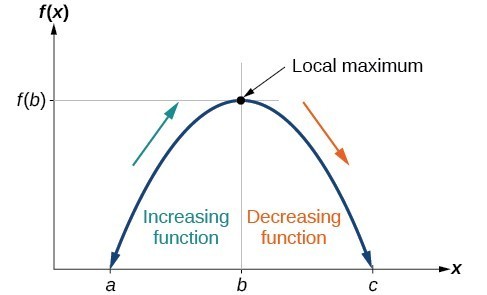Graph of a polynomial that shows the increasing and decreasing intervals and local maximum. Definition of a local maximum.
These observations lead us to a formal definition of local extrema.

A General Note: Local Minima and Local Maxima

A function [latex]f[/latex] is an increasing function on an open interval if [latex]f\left(b\right)>f\left(a\right)[/latex] for any two input values [latex]a[/latex] and [latex]b[/latex] in the given interval where [latex]b>a[/latex]. A function [latex]f[/latex] is a decreasing function on an open interval if [latex]f\left(b\right)<f\left(a\right)[/latex] for any two input values [latex]a[/latex] and [latex]b[/latex] in the given interval where [latex]b>a[/latex]. A function [latex]f[/latex] has a local maximum at [latex]x=b[/latex] if there exists an interval [latex]\left(a,c\right)[/latex] with [latex]a<b<c[/latex] such that, for any [latex]x[/latex] in the interval [latex]\left(a,c\right)[/latex], [latex]f\left(x\right)\le f\left(b\right)[/latex]. Likewise, [latex]f[/latex] has a local minimum at [latex]x=b[/latex] if there exists an interval [latex]\left(a,c\right)[/latex] with [latex]a<b<c[/latex] such that, for any [latex]x[/latex] in the interval [latex]\left(a,c\right)[/latex], [latex]f\left(x\right)\ge f\left(b\right)[/latex].

Example: Finding Increasing and Decreasing Intervals on a Graph

Given the function [latex]p\left(t\right)[/latex] in the graph below, identify the intervals on which the function appears to be increasing.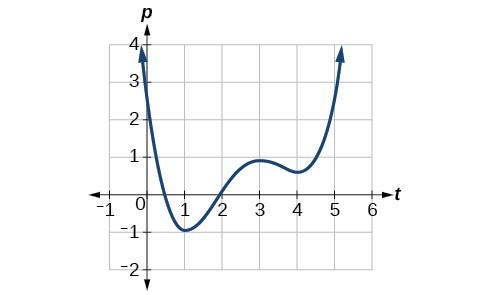 Graph of a polynomial. As x gets large in the negative direction, the outputs of the function get large in the positive direction. As inputs approach 1, then the function value approaches a minimum of negative one. As x approaches 3, the values increase again and between 3 and 4 decrease one last time. As x gets large in the positive direction, the function values increase without bound.

Answer: We see that the function is not constant on any interval. The function is increasing where it slants upward as we move to the right and decreasing where it slants downward as we move to the right. The function appears to be increasing from [latex]t=1[/latex] to [latex]t=3[/latex] and from [latex]t=4[/latex] on. In interval notation, we would say the function appears to be increasing on the interval (1,3) and the interval [latex]\left(4,\infty \right)[/latex].

Analysis of the Solution

Notice in this example that we used open intervals (intervals that do not include the endpoints), because the function is neither increasing nor decreasing at [latex]t=1[/latex] , [latex]t=3[/latex] , and [latex]t=4[/latex] . These points are the local extrema (two minima and a maximum).

Example: Finding Local Maxima and Minima from a Graph

For the function [latex]f[/latex] whose graph is shown below, find all local maxima and minima.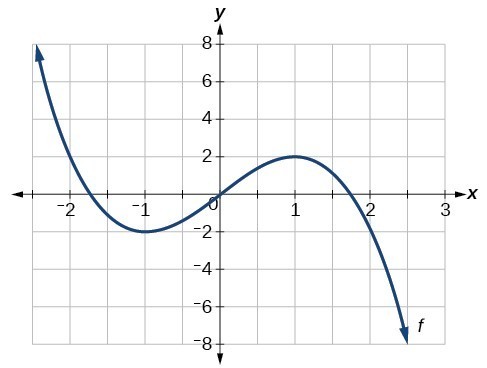 Graph of a polynomial. The line curves down to x = negative 2 and up to x = 1.

Answer: Observe the graph of [latex]f[/latex]. The graph attains a local maximum at [latex]x=1[/latex] because it is the highest point in an open interval around [latex]x=1[/latex]. The local maximum is the [latex]y[/latex] -coordinate at [latex]x=1[/latex], which is [latex]2[/latex]. The graph attains a local minimum at [latex]\text{ }x=-1\text{ }[/latex] because it is the lowest point in an open interval around [latex]x=-1[/latex]. The local minimum is the y-coordinate at [latex]x=-1[/latex], which is [latex]-2[/latex].

Analyzing the Toolkit Functions for Increasing or Decreasing Intervals

We will now return to our toolkit functions and discuss their graphical behavior in the table below.
Function Increasing/Decreasing Example
Constant Function [latex]f\left(x\right)={c}[/latex] Neither increasing nor decreasing
Identity Function [latex]f\left(x\right)={x}[/latex]  Increasing
Quadratic Function [latex]f\left(x\right)={x}^{2}[/latex] Increasing on [latex]\left(0,\infty\right)[/latex] Decreasing on [latex]\left(-\infty,0\right)[/latex] Minimum at [latex]x=0[/latex]
Cubic Function [latex]f\left(x\right)={x}^{3}[/latex] Increasing
 Reciprocal [latex]f\left(x\right)=\frac{1}{x}[/latex] Decreasing [latex]\left(-\infty,0\right)\cup\left(0,\infty\right)[/latex]
Reciprocal Squared [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex] Increasing on [latex]\left(-\infty,0\right)[/latex] Decreasing on [latex]\left(0,\infty\right)[/latex]
Cube Root [latex]f\left(x\right)=\sqrt[3]{x}[/latex] Increasing Screen Shot 2015-08-20 at 8.53.26 AM
Square Root [latex]f\left(x\right)=\sqrt{x}[/latex] Increasing on [latex]\left(0,\infty\right)[/latex]
Absolute Value [latex]f\left(x\right)=|x|[/latex] Increasing on [latex]\left(0,\infty\right)[/latex] Decreasing on [latex]\left(-\infty,0\right)[/latex]

Use a graph to locate the absolute maximum and absolute minimum of a function

There is a difference between locating the highest and lowest points on a graph in a region around an open interval (locally) and locating the highest and lowest points on the graph for the entire domain. The [latex]y\text{-}[/latex] coordinates (output) at the highest and lowest points are called the absolute maximum and absolute minimum, respectively. To locate absolute maxima and minima from a graph, we need to observe the graph to determine where the graph attains it highest and lowest points on the domain of the function.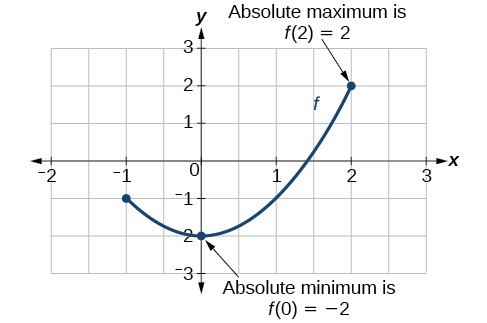 Graph of a segment of a parabola with an absolute minimum at (0, -2) and absolute maximum at (2, 2). Not every function has an absolute maximum or minimum value. The toolkit function [latex]f\left(x\right)={x}^{3}[/latex] is one such function.

A General Note: Absolute Maxima and Minima

The absolute maximum of [latex]f[/latex] at [latex]x=c[/latex] is [latex]f\left(c\right)[/latex] where [latex]f\left(c\right)\ge f\left(x\right)[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex]. The absolute minimum of [latex]f[/latex] at [latex]x=d[/latex] is [latex]f\left(d\right)[/latex] where [latex]f\left(d\right)\le f\left(x\right)[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex].

Example: Finding Absolute Maxima and Minima from a Graph

For the function [latex]f[/latex] shown below, find all absolute maxima and minima.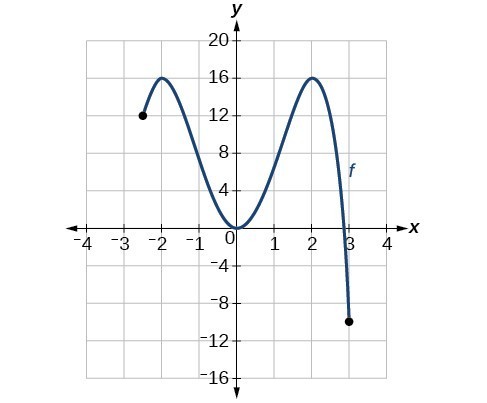 Graph of a polynomial.

Answer: Observe the graph of [latex]f[/latex]. The graph attains an absolute maximum in two locations, [latex]x=-2[/latex] and [latex]x=2[/latex], because at these locations, the graph attains its highest point on the domain of the function. The absolute maximum is the y-coordinate at [latex]x=-2[/latex] and [latex]x=2[/latex], which is [latex]16[/latex]. The graph attains an absolute minimum at [latex]x=3[/latex], because it is the lowest point on the domain of the function’s graph. The absolute minimum is the y-coordinate at [latex]x=3[/latex], which is [latex]-10[/latex].

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 4084. Authored by: Lippman,David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 32572, 32571. Authored by: Smart,Jim. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.