Understand the relationship between degree and turning points
In addition to the end behavior, recall that we can analyze a polynomial function’s local behavior. It may have a turning point where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising). Look at the graph of the polynomial function [latex]f\left(x\right)={x}^{4}-{x}^{3}-4{x}^{2}+4x[/latex] in Figure 11. The graph has three turning points.
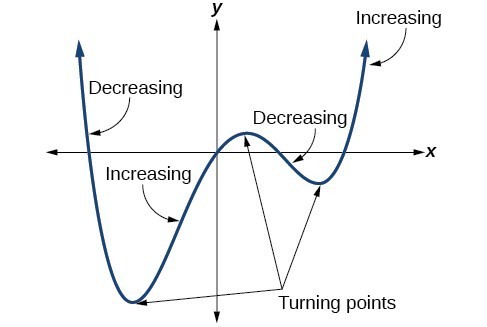 Figure 11
Figure 11This function f is a 4th degree polynomial function and has 3 turning points. The maximum number of turning points of a polynomial function is always one less than the degree of the function.
A General Note: Interpreting Turning Points
A turning point is a point of the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising).
A polynomial of degree n will have at most n – 1 turning points.
Example 7: Finding the Maximum Number of Turning Points Using the Degree of a Polynomial Function
Find the maximum number of turning points of each polynomial function.
- [latex]f\left(x\right)=-{x}^{3}+4{x}^{5}-3{x}^{2}++1[/latex]
- [latex]f\left(x\right)=-{\left(x - 1\right)}^{2}\left(1+2{x}^{2}\right)[/latex]
Solution
- [latex]f\left(x\right)=-x{}^{3}+4{x}^{5}-3{x}^{2}++1[/latex]
First, rewrite the polynomial function in descending order: [latex]f\left(x\right)=4{x}^{5}-{x}^{3}-3{x}^{2}++1[/latex]
Identify the degree of the polynomial function. This polynomial function is of degree 5.
The maximum number of turning points is 5 – 1 = 4.
- [latex]f\left(x\right)=-{\left(x - 1\right)}^{2}\left(1+2{x}^{2}\right)[/latex]
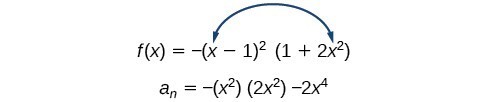 Figure 12
Figure 12First, identify the leading term of the polynomial function if the function were expanded.
Then, identify the degree of the polynomial function. This polynomial function is of degree 4.
The maximum number of turning points is 4 – 1 = 3.
Licenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
