Solving a Rational Equation
In this section, we look at rational equations that, after some manipulation, result in a linear equation. If an equation contains at least one rational expression, it is a considered a rational equation. Recall that a rational number is the ratio of two numbers, such as [latex]\frac{2}{3}[/latex] or [latex]\frac{7}{2}[/latex]. A rational expression is the ratio, or quotient, of two polynomials. Here are three examples.[latex]\frac{x+1}{{x}^{2}-4},\frac{1}{x - 3},\text{ or }\frac{4}{{x}^{2}+x - 2}[/latex]
Rational equations have a variable in the denominator in at least one of the terms.
Our goal is to perform algebraic operations so that the variables appear in the numerator. In fact, we will eliminate all denominators by multiplying both sides of the equation by the least common denominator (LCD).
Finding the LCD is identifying an expression that contains the highest power of all of the factors in all of the denominators. We do this because when the equation is multiplied by the LCD, the common factors in the LCD and in each denominator will equal one and will cancel out.
Example 3: Solving a Rational Equation
Solve the rational equation: [latex]\frac{7}{2x}-\frac{5}{3x}=\frac{22}{3}\\[/latex].Solution
We have three denominators; [latex]2x,3x[/latex], and 3. The LCD must contain [latex]2x,3x[/latex], and 3. An LCD of [latex]6x[/latex] contains all three denominators. In other words, each denominator can be divided evenly into the LCD. Next, multiply both sides of the equation by the LCD [latex]6x[/latex].[latex]\begin{array}{ll}\left(6x\right)\left[\frac{7}{2x}-\frac{5}{3x}\right]\hfill& =\hfill&\left[\frac{22}{3}\right]\left(6x\right)\hfill & \hfill \\ \left(6x\right)\left(\frac{7}{2x}\right)-\left(6x\right)\left(\frac{5}{3x}\right)\hfill& =\hfill&\left(\frac{22}{3}\right)\left(6x\right)\hfill & \text{Use the distributive property}.\hfill \\ \left(\cancel{6x}\right)\left(\frac{7}{\cancel{2x}}\right)-\left(\cancel{6x}\right)\left(\frac{5}{\cancel{3x}}\right)\hfill&=\hfill&\left(\frac{22}{\cancel{3}}\right)\left(\cancel{6}x\right)\hfill & \text{Cancel out the common factors}.\hfill \\ 3\left(7\right)-2\left(5\right)\hfill&=\hfill& 22\left(2x\right)\hfill & \text{Multiply remaining factors by each numerator}.\hfill \\ 21 - 10\hfill& =\hfill& 44x\hfill & \hfill \\ 11\hfill&=\hfill& 44x\hfill & \hfill \\ \frac{11}{44}\hfill& =\hfill& x\hfill & \hfill \\ \frac{1}{4}\hfill& = \hfill& x\hfill & \hfill \end{array}[/latex]
[latex]x\left(x - 1\right)3=3x\left(x - 1\right)[/latex]
So, both sides of the equation would be multiplied by [latex]3x\left(x - 1\right)[/latex]. Leave the LCD in factored form, as this makes it easier to see how each denominator in the problem cancels out.
Another example is a problem with two denominators, such as [latex]x[/latex] and [latex]{x}^{2}+2x[/latex]. Once the second denominator is factored as [latex]{x}^{2}+2x=x\left(x+2\right)[/latex], there is a common factor of x in both denominators and the LCD is [latex]x\left(x+2\right)[/latex].
Sometimes we have a rational equation in the form of a proportion; that is, when one fraction equals another fraction and there are no other terms in the equation.
[latex]\frac{a}{b}=\frac{c}{d}[/latex]
We can use another method of solving the equation without finding the LCD: cross-multiplication. We multiply terms by crossing over the equal sign.
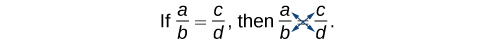 Multiply [latex]a\left(d\right)[/latex] and [latex]b\left(c\right)[/latex], which results in [latex]ad=bc[/latex].
Any solution that makes a denominator in the original expression equal zero must be excluded from the possibilities.
Multiply [latex]a\left(d\right)[/latex] and [latex]b\left(c\right)[/latex], which results in [latex]ad=bc[/latex].
Any solution that makes a denominator in the original expression equal zero must be excluded from the possibilities.
A General Note: Rational Equations
A rational equation contains at least one rational expression where the variable appears in at least one of the denominators.How To: Given a rational equation, solve it.
- Factor all denominators in the equation.
- Find and exclude values that set each denominator equal to zero.
- Find the LCD.
- Multiply the whole equation by the LCD. If the LCD is correct, there will be no denominators left.
- Solve the remaining equation.
- Make sure to check solutions back in the original equations to avoid a solution producing zero in a denominator
Example 4: Solving a Rational Equation without Factoring
Solve the following rational equation:[latex]\frac{2}{x}-\frac{3}{2}=\frac{7}{2x}[/latex]
Solution
We have three denominators: [latex]x[/latex], [latex]2[/latex], and [latex]2x[/latex]. No factoring is required. The product of the first two denominators is equal to the third denominator, so, the LCD is [latex]2x[/latex]. Only one value is excluded from a solution set, [latex]x=0[/latex]. Next, multiply the whole equation (both sides of the equal sign) by [latex]2x[/latex].[latex]\begin{array}{ll}2x\left[\frac{2}{x}-\frac{3}{2}\right]\hfill&=\left[\frac{7}{2x}\right]2x\hfill & \hfill \\ 2\cancel{x}\left(\frac{2}{\cancel{x}}\right)-\cancel{2}x\left(\frac{3}{\cancel{2}}\right)\hfill&=\left(\frac{7}{\cancel{2x}}\right)\cancel{2x}\hfill & \text{Distribute }2x\hfill \\ 2\left(2\right)-3x\hfill&=7\hfill & \text{Denominators cancel out}.\hfill \\ 4 - 3x\hfill&=7\hfill & \hfill \\ -3x\hfill&=3\hfill & \hfill \\ x\hfill&=-1\hfill & \hfill \\ \hfill&\text{ or }\{-1\}\hfill & \hfill \end{array}[/latex]
The proposed solution is [latex]x=-1[/latex], which is not an excluded value, so the solution set contains one number, [latex]x=-1[/latex], or [latex]\{-1\}[/latex] written in set notation.
Try It 3
Solve the rational equation: [latex]\frac{2}{3x}=\frac{1}{4}-\frac{1}{6x}[/latex]. SolutionExample 5: Solving a Rational Equation by Factoring the Denominator
Solve the following rational equation: [latex]\frac{1}{x}=\frac{1}{10}-\frac{3}{4x}[/latex].Solution
First find the common denominator. The three denominators in factored form are [latex]x,10=2\cdot 5[/latex], and [latex]4x=2\cdot 2\cdot x[/latex]. The smallest expression that is divisible by each one of the denominators is [latex]20x[/latex]. Only [latex]x=0[/latex] is an excluded value. Multiply the whole equation by [latex]20x[/latex].[latex]\begin{array}{l}20x\left(\frac{1}{x}\right)=\left(\frac{1}{10}-\frac{3}{4x}\right)20x\hfill \\ 20=2x - 15\hfill \\ 35=2x\hfill \\ \frac{35}{2}=x\hfill \end{array}[/latex]
The solution is [latex]x=\frac{35}{2}[/latex].
Try It 4
Solve the rational equation: [latex]-\frac{5}{2x}+\frac{3}{4x}=-\frac{7}{4}[/latex]. SolutionExample 6: Solving Rational Equations with a Binomial in the Denominator
Solve the following rational equations and state the excluded values:- [latex]\frac{3}{x - 6}=\frac{5}{x}[/latex]
- [latex]\frac{x}{x - 3}=\frac{5}{x - 3}-\frac{1}{2}[/latex]
- [latex]\frac{x}{x - 2}=\frac{5}{x - 2}-\frac{1}{2}[/latex]
Solution
- The denominators [latex]x[/latex] and [latex]x - 6[/latex] have nothing in common. Therefore, the LCD is the product [latex]x\left(x - 6\right)[/latex]. However, for this problem, we can cross-multiply.
[latex]\begin{array}{l}\frac{3}{x - 6}=\frac{5}{x}\hfill \\ 3x=5\left(x - 6\right)\text{Distribute}.\hfill \\ 3x=5x - 30\hfill \\ -2x=-30\hfill \\ x=15\hfill \end{array}[/latex]The solution is [latex]x=15[/latex]. The excluded values are [latex]x=6[/latex] and [latex]x=0[/latex].
- The LCD is [latex]2\left(x - 3\right)[/latex]. Multiply both sides of the equation by [latex]2\left(x - 3\right)[/latex].
[latex]\begin{array}{l}2\left(x - 3\right)\left[\frac{x}{x - 3}\right]\hfill&=\left[\frac{5}{x - 3}-\frac{1}{2}\right]2\left(x - 3\right)\hfill \\ \frac{2\cancel{\left(x - 3\right)}x}{\cancel{x - 3}}\hfill&=\frac{2\cancel{\left(x - 3\right)}5}{\cancel{x - 3}}-\frac{\cancel{2}\left(x - 3\right)}{\cancel{2}}\hfill \\ 2x\hfill&=10-\left(x - 3\right)\hfill \\ 2x\hfill&=10-x+3\hfill \\ 2x\hfill&=13-x\hfill \\ 3x\hfill&=13\hfill \\ x\hfill&=\frac{13}{3}\hfill \end{array}[/latex]The solution is [latex]x=\frac{13}{3}[/latex]. The excluded value is [latex]x=3[/latex].
- The least common denominator is [latex]2\left(x - 2\right)[/latex]. Multiply both sides of the equation by [latex]x\left(x - 2\right)[/latex].
[latex]\begin{array}{l}2\left(x - 2\right)\left[\frac{x}{x - 2}\right]=\left[\frac{5}{x - 2}-\frac{1}{2}\right]2\left(x - 2\right)\hfill \\ 2x=10-\left(x - 2\right)\hfill \\ 2x=12-x\hfill \\ 3x=12\hfill \\ x=4\hfill \end{array}[/latex]The solution is [latex]x=4[/latex]. The excluded value is [latex]x=2[/latex].
Try It 5
Solve [latex]\frac{-3}{2x+1}=\frac{4}{3x+1}[/latex]. State the excluded values. SolutionExample 7: Solving a Rational Equation with Factored Denominators and Stating Excluded Values
Solve the rational equation after factoring the denominators: [latex]\frac{2}{x+1}-\frac{1}{x - 1}=\frac{2x}{{x}^{2}-1}[/latex]. State the excluded values.Solution
We must factor the denominator [latex]{x}^{2}-1[/latex]. We recognize this as the difference of squares, and factor it as [latex]\left(x - 1\right)\left(x+1\right)[/latex]. Thus, the LCD that contains each denominator is [latex]\left(x - 1\right)\left(x+1\right)[/latex]. Multiply the whole equation by the LCD, cancel out the denominators, and solve the remaining equation.[latex]\begin{array}{l}\left(x - 1\right)\left(x+1\right)\left[\frac{2}{x+1}-\frac{1}{x - 1}\right]\hfill&=\left[\frac{2x}{\left(x - 1\right)\left(x+1\right)}\right]\left(x - 1\right)\left(x+1\right)\hfill \\ 2\left(x - 1\right)-1\left(x+1\right)\hfill&=2x\hfill \\ 2x - 2-x - 1\hfill&=2x\hfill&\text{Distribute the negative sign}.\hfill \\ -3-x\hfill&=0\hfill \\ -3\hfill&=x\hfill \end{array}[/latex]
The solution is [latex]x=-3[/latex]. The excluded values are [latex]x=1[/latex] and [latex]x=-1[/latex].
Try It 6
Solve the rational equation: [latex]\frac{2}{x - 2}+\frac{1}{x+1}=\frac{1}{{x}^{2}-x - 2}[/latex]. SolutionLicenses & Attributions
CC licensed content, Specific attribution
- College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
