We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Identifying the Degree and Leading Coefficient of Polynomials

The formula just found is an example of a polynomial, which is a sum of or difference of terms, each consisting of a variable raised to a nonnegative integer power. A number multiplied by a variable raised to an exponent, such as [latex]384\pi [/latex], is known as a coefficient. Coefficients can be positive, negative, or zero, and can be whole numbers, decimals, or fractions. Each product [latex]{a}_{i}{x}^{i}[/latex], such as [latex]384\pi w[/latex], is a term of a polynomial. If a term does not contain a variable, it is called a constant. A polynomial containing only one term, such as [latex]5{x}^{4}[/latex], is called a monomial. A polynomial containing two terms, such as [latex]2x - 9[/latex], is called a binomial. A polynomial containing three terms, such as [latex]-3{x}^{2}+8x - 7[/latex], is called a trinomial. We can find the degree of a polynomial by identifying the highest power of the variable that occurs in the polynomial. The term with the highest degree is called the leading term because it is usually written first. The coefficient of the leading term is called the leading coefficient. When a polynomial is written so that the powers are descending, we say that it is in standard form.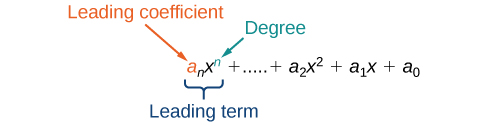 A polynomial reading: a sub n times x to the nth power plus and so on plus a sub 2 times x squared plus a sub one times x plus a subzero is shown. The a in the term a sub n is labeled: leading coefficient. The n in the term x to the nth power is labeled: degree. Finally, the entire term is labeled as: Leading term.

A General Note: Polynomials

A polynomial is an expression that can be written in the form
[latex]{a}_{n}{x}^{n}+\dots+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}[/latex]
Each real number aiis called a coefficient. The number [latex]{a}_{0}[/latex] that is not multiplied by a variable is called a constant. Each product [latex]{a}_{i}{x}^{i}[/latex] is a term of a polynomial. The highest power of the variable that occurs in the polynomial is called the degree of a polynomial. The leading term is the term with the highest power, and its coefficient is called the leading coefficient.

How To: Given a polynomial expression, identify the degree and leading coefficient.

  1. Find the highest power of x to determine the degree.
  2. Identify the term containing the highest power of x to find the leading term.
  3. Identify the coefficient of the leading term.

Example 1: Identifying the Degree and Leading Coefficient of a Polynomial

For the following polynomials, identify the degree, the leading term, and the leading coefficient.
  1. [latex]3+2{x}^{2}-4{x}^{3}\\[/latex]
  2. [latex]5{t}^{5}-2{t}^{3}+7t[/latex]
  3. [latex]6p-{p}^{3}-2[/latex]

Solution

  1. The highest power of x is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-4{x}^{3}[/latex]. The leading coefficient is the coefficient of that term, [latex]-4[/latex].
  2. The highest power of t is [latex]5[/latex], so the degree is [latex]5[/latex]. The leading term is the term containing that degree, [latex]5{t}^{5}[/latex]. The leading coefficient is the coefficient of that term, [latex]5[/latex].
  3. The highest power of p is [latex]3[/latex], so the degree is [latex]3[/latex]. The leading term is the term containing that degree, [latex]-{p}^{3}[/latex], The leading coefficient is the coefficient of that term, [latex]-1[/latex].

Try It 1

Identify the degree, leading term, and leading coefficient of the polynomial [latex]4{x}^{2}-{x}^{6}+2x - 6[/latex]. Solution

Licenses & Attributions

CC licensed content, Specific attribution