Graph logarithmic functions
Now that we have a feel for the set of values for which a logarithmic function is defined, we move on to graphing logarithmic functions. The family of logarithmic functions includes the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] along with all its transformations: shifts, stretches, compressions, and reflections.
We begin with the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex]. Because every logarithmic function of this form is the inverse of an exponential function with the form [latex]y={b}^{x}[/latex], their graphs will be reflections of each other across the line [latex]y=x[/latex]. To illustrate this, we can observe the relationship between the input and output values of [latex]y={2}^{x}[/latex] and its equivalent [latex]x={\mathrm{log}}_{2}\left(y\right)[/latex] in the table below.
| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| [latex]{2}^{x}=y[/latex] | [latex]\frac{1}{8}[/latex] | [latex]\frac{1}{4}[/latex] | [latex]\frac{1}{2}[/latex] | 1 | 2 | 4 | 8 |
| [latex]{\mathrm{log}}_{2}\left(y\right)=x[/latex] | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
Using the inputs and outputs from the table above, we can build another table to observe the relationship between points on the graphs of the inverse functions [latex]f\left(x\right)={2}^{x}[/latex] and [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex].
| [latex]f\left(x\right)={2}^{x}[/latex] | [latex]\left(-3,\frac{1}{8}\right)[/latex] | [latex]\left(-2,\frac{1}{4}\right)[/latex] | [latex]\left(-1,\frac{1}{2}\right)[/latex] | [latex]\left(0,1\right)[/latex] | [latex]\left(1,2\right)[/latex] | [latex]\left(2,4\right)[/latex] | [latex]\left(3,8\right)[/latex] |
| [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex] | [latex]\left(\frac{1}{8},-3\right)[/latex] | [latex]\left(\frac{1}{4},-2\right)[/latex] | [latex]\left(\frac{1}{2},-1\right)[/latex] | [latex]\left(1,0\right)[/latex] | [latex]\left(2,1\right)[/latex] | [latex]\left(4,2\right)[/latex] | [latex]\left(8,3\right)[/latex] |
As we’d expect, the x- and y-coordinates are reversed for the inverse functions. The figure below shows the graph of f and g.
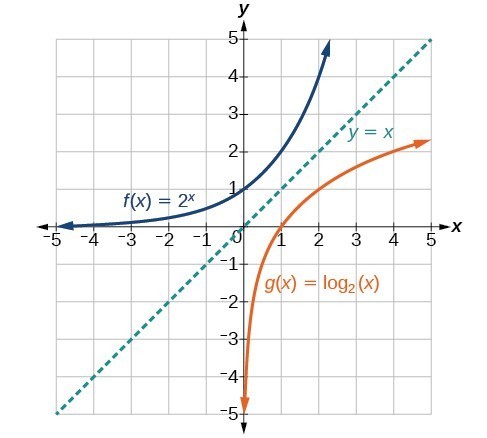
Figure 2. Notice that the graphs of [latex]f\left(x\right)={2}^{x}[/latex] and [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex] are reflections about the line y = x.
Observe the following from the graph:
- [latex]f\left(x\right)={2}^{x}[/latex] has a y-intercept at [latex]\left(0,1\right)[/latex] and [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex] has an x-intercept at [latex]\left(1,0\right)[/latex].
- The domain of [latex]f\left(x\right)={2}^{x}[/latex], [latex]\left(-\infty ,\infty \right)[/latex], is the same as the range of [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex].
- The range of [latex]f\left(x\right)={2}^{x}[/latex], [latex]\left(0,\infty \right)[/latex], is the same as the domain of [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex].
A General Note: Characteristics of the Graph of the Parent Function, f(x) = logb(x)
For any real number x and constant b > 0, [latex]b\ne 1[/latex], we can see the following characteristics in the graph of [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex]:
- one-to-one function
- vertical asymptote: x = 0
- domain: [latex]\left(0,\infty \right)[/latex]
- range: [latex]\left(-\infty ,\infty \right)[/latex]
- x-intercept: [latex]\left(1,0\right)[/latex] and key point [latex]\left(b,1\right)[/latex]
- y-intercept: none
- increasing if [latex]b>1[/latex]
- decreasing if 0 < b < 1
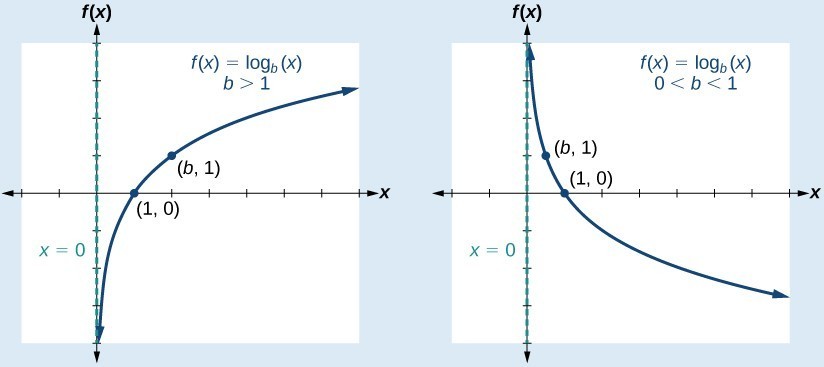 Figure 3
Figure 3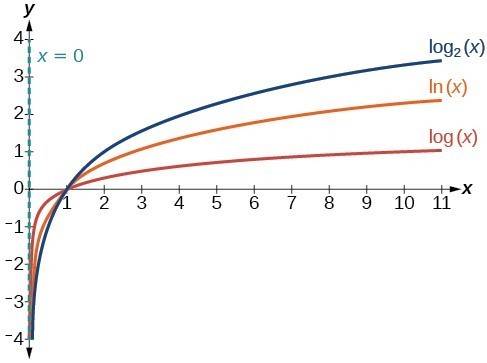 Figure 4. The graphs of three logarithmic functions with different bases, all greater than 1.
Figure 4. The graphs of three logarithmic functions with different bases, all greater than 1.How To: Given a logarithmic function with the form [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex], graph the function.
- Draw and label the vertical asymptote, x = 0.
- Plot the x-intercept, [latex]\left(1,0\right)[/latex].
- Plot the key point [latex]\left(b,1\right)[/latex].
- Draw a smooth curve through the points.
- State the domain, [latex]\left(0,\infty \right)[/latex], the range, [latex]\left(-\infty ,\infty \right)[/latex], and the vertical asymptote, x = 0.
Example 3: Graphing a Logarithmic Function with the Form [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex].
Graph [latex]f\left(x\right)={\mathrm{log}}_{5}\left(x\right)[/latex]. State the domain, range, and asymptote.
Solution
Before graphing, identify the behavior and key points for the graph.
- Since b = 5 is greater than one, we know the function is increasing. The left tail of the graph will approach the vertical asymptote x = 0, and the right tail will increase slowly without bound.
- The x-intercept is [latex]\left(1,0\right)[/latex].
- The key point [latex]\left(5,1\right)[/latex] is on the graph.
- We draw and label the asymptote, plot and label the points, and draw a smooth curve through the points.
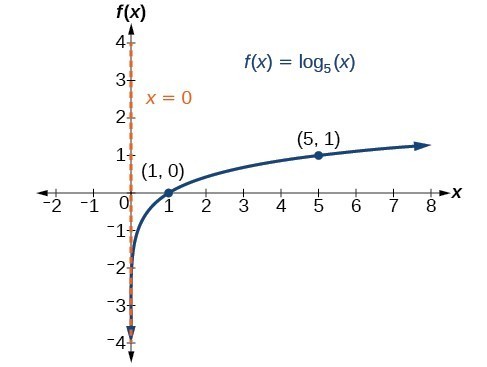
Figure 5. The domain is [latex]\left(0,\infty \right)[/latex], the range is [latex]\left(-\infty ,\infty \right)[/latex], and the vertical asymptote is x = 0.
Try It 3
Graph [latex]f\left(x\right)={\mathrm{log}}_{\frac{1}{5}}\left(x\right)[/latex]. State the domain, range, and asymptote.
SolutionLicenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
