Rational Expressions and Functions
Learning Objectives
- Recognize and define a rational expression
- Determine the domain of a rational expression
- Simplify a rational expression
- Rational functions
Determine the domain of a rational expression
One sure way you can break math is to divide by zero. Consider the following rational expression evaluated at x = 2:Evaluate [latex]\displaystyle \frac{x}{x-2}[/latex] for [latex]x=2[/latex]
Substitute [latex]x=2[/latex]
[latex]\displaystyle \begin{array}{l}\frac{2}{2-2}\\\text{}\\=\frac{2}{0}\end{array}[/latex]
This means that for the expression [latex]\displaystyle \frac{x}{x-2}[/latex], x cannot be 2 because it will result in an undefined ratio. In general, finding values for a variable that will not result in division by zero is called finding the domain. Finding the domain of a rational expression or function will help you not break math.Domain of a rational expression or equation
The domain of a rational expression or equation is a collection of the values for the variable that will not result in an undefined mathematical operation such as division by zero. For a = any real number, we can notate the domain in the following way:x is all real numbers where [latex]x\neq{a}[/latex]
Example
Identify the domain of the expression. [latex]\displaystyle \frac{x+7}{{{x}^{2}}+8x-9}[/latex]Answer: Find any values for x that would make the denominator equal to 0 by setting the denominator equal to 0 and solving the equation.
[latex]x^{2}+8x-9=0[/latex]
Solve the equation by factoring. The solutions are the values that are excluded from the domain.[latex]\begin{array}{c}(x+9)(x-1)=0\\x=-9\,\,\,\text{or}\,\,\,x=1\end{array}[/latex]
Answer
The domain is all real numbers except [latex]−9[/latex] and [latex]1[/latex].Simplify Rational Expressions
Before we dive in to simplifying rational expressions, let's review the difference between a factor, a term, and an expression. This will hopefully help you avoid another way to break math when you are simplifying rational expressions. Factors are the building blocks of multiplication. They are the numbers that you can multiply together to produce another number: 2 and 10 are factors of 20, as are 4, 5, 1, 20. Terms are single numbers, or variables and numbers connected by multiplication. -4, 6x and [latex]x^2[/latex] are all terms. Expressions are groups of terms connected by addition and subtraction. [latex]2x^2-5[/latex] is an expression. This distinction is important when you are required to divide. Let's use an example to show why this is important. Simplify: [latex]\displaystyle \large\frac{2x^2}{12x}[/latex] The numerator and denominator of this fraction consist of factors. To simplify it, we can divide without being impeded by addition or subtraction.[latex]\displaystyle \begin{array}{cc}\Large\frac{2x^2}{12x}\\=\Large\frac{2\cdot{x}\cdot{x}}{2\cdot3\cdot2\cdot{x}}\\=\Large\frac{\cancel{2}\cdot{\cancel{x}}\cdot{x}}{\cancel{2}\cdot3\cdot2\cdot{\cancel{x}}}\end{array}[/latex]
We can do this because [latex]\displaystyle \frac{2}{2}=1\text{ and }\frac{x}{x}=1[/latex], so our expression simplifies to [latex]\displaystyle \large\frac{x}{6}[/latex]
Compare that to the expression [latex]\displaystyle \large\frac{2x^2+x}{12-2x}[/latex], notice the denominator and numerator consist of two terms connected by addition and subtraction. We have to tip-toe around the addition and subtraction. When asked to simplify it is tempting to want to cancel out like terms as we did when we just had factors. But you can't do that, it will break math! Breaking Math
Breaking MathExample
Simplify and state the domain for the expression. [latex]\displaystyle \frac{x+3}{{{x}^{2}}+12x+27}[/latex]Answer: To find the domain (and the excluded values), find the values for which the denominator is equal to 0. Factor the quadratic, and apply the zero product principle.
[latex]\begin{array}{c}x+3=0\,\,\,\,\,\,\text{or}\,\,\,\,\,\,x+9=0\\x=0-3\,\,\,\,\,\,\text{or}\,\,\,\,\,\,x=0-9\\x=-3\,\,\,\,\,\,\text{or}\,\,\,\,\,\,x=-9\\\\x=-3\,\,\,\,\,\,\text{or}\,\,\,\,\,\,x=-9\end{array}[/latex]
The domain is all real numbers except [latex]x=-3[/latex] or [latex]x=-9[/latex]. Factor the numerator and denominator. Identify the factors that are the same in the numerator and denominator, and simplify.[latex]\displaystyle \large\begin{array}{c}\frac{x+3}{x^{2}+12x+27}\\\\=\frac{x+3}{\left(x+3\right)\left(x+9\right)}\\\\\frac{\cancel{x+3}}{\cancel{\left(x+3\right)}\left(x+9\right)}\\\\\normalsize=1\cdot\large\frac{1}{x+9}\end{array}[/latex]
Answer
[latex-display]\displaystyle \frac{x+3}{{{x}^{2}}+12x+27}=\frac{1}{x+9}[/latex-display] The domain is all real numbers except [latex]−3[/latex] and [latex]−9[/latex].Example
Simplify and state the domain for the expression. [latex]\displaystyle \frac{x^{2}+10x+24}{x^{3}-x^{2}-20x}[/latex]Answer: To find the domain, determine the values for which the denominator is equal to 0.
[latex]\begin{array}{r}x^{3}-x^{2}-20x=0\\x\left(x^{2}-x-20\right)=0\\x\left(x-5\right)\left(x+4\right)=0\end{array}[/latex]
The domain is all real numbers except 0, 5, and −4. To simplify, factor the numerator and denominator of the rational expression. Identify the factors that are the same in the numerator and denominator, and simplify.[latex]\displaystyle \large\begin{array}{c}\frac{x^{2}+10x+24}{x^{3}-x^{2}-20x}\\\\=\frac{\left(x+4\right)\left(x+6\right)}{x\left(x-5\right)\left(x+4\right)}\\\\=\frac{\cancel{\left(x+4\right)}\left(x+6\right)}{x\left(x-5\right)\cancel{\left(x+4\right)}}\end{array}[/latex]
Simplify. It is acceptable to either leave the denominator in factored form or to distribute multiplication.[latex]\displaystyle \frac{x+6}{x\left(x-5\right)}\,\,\,\text{or}\,\,\,\frac{x+6}{x^{2}-5x}[/latex]
Answer
[latex-display] \displaystyle \frac{x+6}{x(x-5)}[/latex] or [latex] \frac{x+6}{{{x}^{2}}-5x}[/latex-display] The domain is all real numbers except 0, 5, and [latex]−4[/latex].Example
Simplify [latex]\displaystyle \frac{{x}^{2}-9}{{x}^{2}+4x+3}[/latex], state the domain.Answer: The special product in the numerator is a difference of squares. [latex-display]\displaystyle \begin{array}\frac{\left(x+3\right)\left(x - 3\right)}{\left(x+3\right)\left(x+1\right)}\hfill & \hfill & \hfill & \hfill & \text{Factor the numerator and the denominator}.\hfill \\ \frac{x - 3}{x+1}\hfill & \hfill & \hfill & \hfill & \text{Cancel common factor }\left(x+3\right).\hfill \end{array}[/latex-display] With the denominator factored it is easier to find the domain of the expression. Determine the values for which the denominator is equal to 0. [latex-display]\begin{array}{cc}\left(x+3\right)=0,\left(x+1\right)=0\\x\ne-3,\text{ AND }x\ne-1\end{array}[/latex-display]
Answer
[latex-display]\displaystyle \frac{{x}^{2}-9}{{x}^{2}+4x+3}=\frac{x - 3}{x+1}[/latex], Domain: [latex]x\ne-3,\text{ AND }x\ne-1[/latex-display]Steps for Simplifying a Rational Expression
To simplify a rational expression, follow these steps:- Determine the domain. The excluded values are those values for the variable that result in the expression having a denominator of 0.
- Factor the numerator and denominator.
- Find common factors for the numerator and denominator and simplify.
Rational Functions
We started this section stating that a rational expression is an expression of the form [latex]\displaystyle \frac{p}{q} [/latex] where [latex]p[/latex] and [latex]q[/latex] are polynomials and [latex]q(x) \neq 0.[/latex] Similarly, we define a rational function as a function of the form:[latex]\displaystyle R(x) = \frac{p(x)}{q(x)}[/latex]
where [latex]p(x)[/latex] and [latex]q(x)[/latex] are polynomial functions and [latex]q(x)[/latex] is not zero. The domain of a rational function is all real numbers except for those values that would cause division by zero. We must eliminate any values that make [latex]q(x) = 0[/latex]. For example, [latex]\displaystyle f(x) = \frac{1}{x}[/latex] and [latex]\displaystyle f(x) = \frac{1}{x^2}[/latex] are examples of rational functions.Finding the domain of rational functions
For the rational function [latex]f\left(x\right)=\frac{1}{x}[/latex] (also called the reciprocal function), we cannot divide by 0, so we must exclude 0 from the domain. Further, 1 divided by any value can never be 0, so the range also will not include 0. In set-builder notation, we could also write [latex]\left\{x|\text{ }x\ne 0\right\}[/latex], the set of all real numbers that are not zero.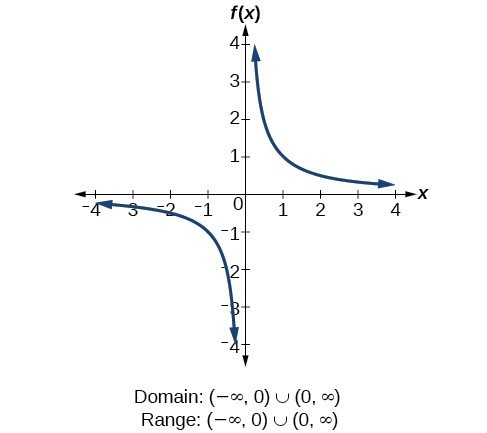 For the rational function [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex], we cannot divide by [latex]0[/latex], so we must exclude [latex]0[/latex] from the domain. There is also no [latex]x[/latex] that can give an output of 0, so 0 is excluded from the range as well. Note that the output of this function is always positive due to the square in the denominator, so the range includes only positive numbers.
For the rational function [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex], we cannot divide by [latex]0[/latex], so we must exclude [latex]0[/latex] from the domain. There is also no [latex]x[/latex] that can give an output of 0, so 0 is excluded from the range as well. Note that the output of this function is always positive due to the square in the denominator, so the range includes only positive numbers.
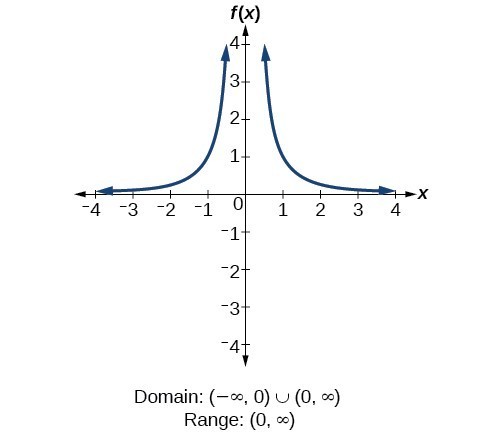
How To: Given a rational function, find the domain.
- Identify the input values.
- Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for [latex]x[/latex] . If the function’s formula contains an even root, set the radicand greater than or equal to 0, and then solve.
- Write the domain in interval form, making sure to exclude any restricted values from the domain.
Example: Finding the Domain of a Rational Function
Find the domain of the function [latex]\displaystyle f\left(x\right)=\frac{x+1}{2-x}[/latex].Answer: When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for [latex]x[/latex].
[latex]\begin{cases}2-x=0\hfill \\ -x=-2\hfill \\ x=2\hfill \end{cases}[/latex]
Now, we will exclude 2 from the domain. The answers are all real numbers where [latex]x<2[/latex] or [latex]x>2[/latex]. We can use a symbol known as the union, [latex]\cup [/latex], to combine the two sets. In interval notation, we write the solution: [latex]\left(\mathrm{-\infty },2\right)\cup \left(2,\infty \right)[/latex].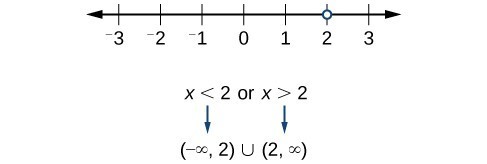 In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,2\right)\cup \left(2,\infty \right)[/latex].
In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,2\right)\cup \left(2,\infty \right)[/latex].
Example
Find the domain of the function: [latex]\displaystyle f\left(x\right)=\frac{1+4x}{2x - 1}[/latex].Answer: [latex]\left(-\infty ,\frac{1}{2}\right)\cup \left(\frac{1}{2},\infty \right)[/latex]
Try It!
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Unit 15: Rational Expressions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
- Simplify and Give the Domain of Rational Expressions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- College Algebra. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: Public Domain: No Known Copyright. License terms: Download for free at :http://cnx.org/contents/[email protected]:1/Preface.
- Question ID#61836. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
