We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra: Co-requisite Course

Counting Principles*

A new company sells customizable cases for tablets and smartphones. Each case comes in a variety of colors and can be personalized for an additional fee with images or a monogram. A customer can choose not to personalize or could choose to have one, two, or three images or a monogram. The customer can choose the order of the images and the letters in the monogram. The company is working with an agency to develop a marketing campaign with a focus on the huge number of options they offer. Counting the possibilities is challenging! We encounter a wide variety of counting problems every day. There is a branch of mathematics devoted to the study of counting problems such as this one. Other applications of counting include secure passwords, horse racing outcomes, and college scheduling choices. We will examine this type of mathematics in this section.

Permutations

Using the Addition Principle

The company that sells customizable cases offers cases for tablets and smartphones. There are 3 supported tablet models and 5 supported smartphone models. The Addition Principle tells us that we can add the number of tablet options to the number of smartphone options to find the total number of options. By the Addition Principle, there are 8 total options. The addition of 3 iPods and 4 iPhones.

A General Note: The Addition Principle

According to the Addition Principle, if one event can occur in [latex]m[/latex] ways and a second event with no common outcomes can occur in [latex]n[/latex] ways, then the first or second event can occur in [latex]m+n[/latex] ways.

Example: Using the Addition Principle

There are 2 vegetarian entrée options and 5 meat entrée options on a dinner menu. What is the total number of entrée options?

Answer: We can add the number of vegetarian options to the number of meat options to find the total number of entrée options. The addition of the type of options for an entree. There are 7 total options.

Try It

A student is shopping for a new computer. He is deciding among 3 desktop computers and 4 laptop computers. What is the total number of computer options?

Answer: 7

Using the Multiplication Principle

The Multiplication Principle applies when we are making more than one selection. Suppose we are choosing an appetizer, an entrée, and a dessert. If there are 2 appetizer options, 3 entrée options, and 2 dessert options on a fixed-price dinner menu, there are a total of 12 possible choices of one each as shown in the tree diagram. A tree diagram of the different menu combinations. The possible choices are:
  1. soup, chicken, cake
  2. soup, chicken, pudding
  3. soup, fish, cake
  4. soup, fish, pudding
  5. soup, steak, cake
  6. soup, steak, pudding
  7. salad, chicken, cake
  8. salad, chicken, pudding
  9. salad, fish, cake
  10. salad, fish, pudding
  11. salad, steak, cake
  12. salad, steak, pudding
We can also find the total number of possible dinners by multiplying. We could also conclude that there are 12 possible dinner choices simply by applying the Multiplication Principle. Number of appetizer options (2) times number of entree options (3) times number of dessert options (2)

A General Note: The Multiplication Principle

According to the Multiplication Principle, if one event can occur in [latex]m[/latex] ways and a second event can occur in [latex]n[/latex] ways after the first event has occurred, then the two events can occur in [latex]m\times n[/latex] ways. This is also known as the Fundamental Counting Principle.

Example: Using the Multiplication Principle

Diane packed 2 skirts, 4 blouses, and a sweater for her business trip. She will need to choose a skirt and a blouse for each outfit and decide whether to wear the sweater. Use the Multiplication Principle to find the total number of possible outfits.

Answer: To find the total number of outfits, find the product of the number of skirt options, the number of blouse options, and the number of sweater options. The multiplication of number of skirt options (2) times the number of blouse options (4) times the number of sweater options (2) which equals 16. There are 16 possible outfits.

Try It

A restaurant offers a breakfast special that includes a breakfast sandwich, a side dish, and a beverage. There are 3 types of breakfast sandwiches, 4 side dish options, and 5 beverage choices. Find the total number of possible breakfast specials.

Answer: There are 60 possible breakfast specials.

The Multiplication Principle can be used to solve a variety of problem types. One type of problem involves placing objects in order. We arrange letters into words and digits into numbers, line up for photographs, decorate rooms, and more. An ordering of objects is called a permutation.

Finding the Number of Permutations of n Distinct Objects Using the Multiplication Principle

To solve permutation problems, it is often helpful to draw line segments for each option. That enables us to determine the number of each option so we can multiply. For instance, suppose we have four paintings, and we want to find the number of ways we can hang three of the paintings in order on the wall. We can draw three lines to represent the three places on the wall. There are four options for the first place, so we write a 4 on the first line. Four times two blanks spots. After the first place has been filled, there are three options for the second place so we write a 3 on the second line. Four times three times one blank spot. After the second place has been filled, there are two options for the third place so we write a 2 on the third line. Finally, we find the product. There are 24 possible permutations of the paintings.

How To: Given [latex]n[/latex] distinct options, determine how many permutations there are.

  1. Determine how many options there are for the first situation.
  2. Determine how many options are left for the second situation.
  3. Continue until all of the spots are filled.
  4. Multiply the numbers together.

Example: Finding the Number of Permutations Using the Multiplication Principle

At a swimming competition, nine swimmers compete in a race.
  1. How many ways can they place first, second, and third?
  2. How many ways can they place first, second, and third if a swimmer named Ariel wins first place? (Assume there is only one contestant named Ariel.)
  3. How many ways can all nine swimmers line up for a photo?

Answer:

  1. Draw lines for each place.There are 9 options for first place. Once someone has won first place, there are 8 remaining options for second place. Once first and second place have been won, there are 7 remaining options for third place.Multiply to find that there are 504 ways for the swimmers to place.
  2. Draw lines for describing each place.We know Ariel must win first place, so there is only 1 option for first place. There are 8 remaining options for second place, and then 7 remaining options for third place.Multiply to find that there are 56 ways for the swimmers to place if Ariel wins first.
  3. Draw lines for describing each place in the photo.There are 9 choices for the first spot, then 8 for the second, 7 for the third, 6 for the fourth, and so on until only 1 person remains for the last spot.There are 362,880 possible permutations for the swimmers to line up.

Analysis of the Solution

Note that in part c, we found there were 9! ways for 9 people to line up. The number of permutations of [latex]n[/latex] distinct objects can always be found by [latex]n![/latex].

Try It

A family of five is having portraits taken. Use the Multiplication Principle to find the following. How many ways can the family line up for the portrait?

Answer: 120

How many ways can the photographer line up 3 family members?

Answer: 60

How many ways can the family line up for the portrait if the parents are required to stand on each end?

Answer: 12

Finding the Number of Permutations of n Distinct Objects Using a Formula

For some permutation problems, it is inconvenient to use the Multiplication Principle because there are so many numbers to multiply. Fortunately, we can solve these problems using a formula. Before we learn the formula, let’s look at two common notations for permutations. If we have a set of [latex]n[/latex] objects and we want to choose [latex]r[/latex] objects from the set in order, we write [latex]P\left(n,r\right)[/latex]. Another way to write this is [latex]{n}_{}{P}_{r}[/latex], a notation commonly seen on computers and calculators. To calculate [latex]P\left(n,r\right)[/latex], we begin by finding [latex]n![/latex], the number of ways to line up all [latex]n[/latex] objects. We then divide by [latex]\left(n-r\right)![/latex] to cancel out the [latex]\left(n-r\right)[/latex] items that we do not wish to line up. Let’s see how this works with a simple example. Imagine a club of six people. They need to elect a president, a vice president, and a treasurer. Six people can be elected president, any one of the five remaining people can be elected vice president, and any of the remaining four people could be elected treasurer. The number of ways this may be done is [latex]6\times 5\times 4=120[/latex]. Using factorials, we get the same result.

[latex]\frac{6!}{3!}=\frac{6\cdot 5\cdot 4\cdot 3!}{3!}=6\cdot 5\cdot 4=120[/latex]

There are 120 ways to select 3 officers in order from a club with 6 members. We refer to this as a permutation of 6 taken 3 at a time. The general formula is as follows.

[latex]P\left(n,r\right)=\frac{n!}{\left(n-r\right)!}[/latex]

Note that the formula stills works if we are choosing all [latex]n[/latex] objects and placing them in order. In that case we would be dividing by [latex]\left(n-n\right)![/latex] or [latex]0![/latex], which we said earlier is equal to 1. So the number of permutations of [latex]n[/latex] objects taken [latex]n[/latex] at a time is [latex]\frac{n!}{1}[/latex] or just [latex]n!\text{.}[/latex]

A General Note: Formula for Permutations of n Distinct Objects

Given [latex]n[/latex] distinct objects, the number of ways to select [latex]r[/latex] objects from the set in order is

[latex]P\left(n,r\right)=\frac{n!}{\left(n-r\right)!}[/latex]

How To: Given a word problem, evaluate the possible permutations.

  1. Identify [latex]n[/latex] from the given information.
  2. Identify [latex]r[/latex] from the given information.
  3. Replace [latex]n[/latex] and [latex]r[/latex] in the formula with the given values.
  4. Evaluate.

Example: Finding the Number of Permutations Using the Formula

A professor is creating an exam of 9 questions from a test bank of 12 questions. How many ways can she select and arrange the questions?

Answer: Substitute [latex]n=12[/latex] and [latex]r=9[/latex] into the permutation formula and simplify.

[latex]\begin{array}{l}\text{ }P\left(n,r\right)=\frac{n!}{\left(n-r\right)!}\hfill \\ P\left(12,9\right)=\frac{12!}{\left(12 - 9\right)!}=\frac{12!}{3!}=79\text{,}833\text{,}600\hfill \end{array}[/latex]

There are 79,833,600 possible permutations of exam questions!

Analysis of the Solution

We can also use a calculator to find permutations. For this problem, we would enter 15, press the [latex]{}_{n}{P}_{r}[/latex] function, enter 12, and then press the equal sign. The [latex]{}_{n}{P}_{r}[/latex] function may be located under the MATH menu with probability commands.

Q & A

Could we have solved  using the Multiplication Principle?

Yes. We could have multiplied [latex]15\cdot 14\cdot 13\cdot 12\cdot 11\cdot 10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4[/latex] to find the same answer.

Try It

A play has a cast of 7 actors preparing to make their curtain call. Use the permutation formula to find the following. How many ways can the 7 actors line up?

Answer: [latex]P\left(7,7\right)=5,040[/latex]

How many ways can 5 of the 7 actors be chosen to line up?

Answer: [latex]P\left(7,5\right)=2,520[/latex]

Finding the Number of Permutations of n Non-Distinct Objects

We have studied permutations where all of the objects involved were distinct. What happens if some of the objects are indistinguishable? For example, suppose there is a sheet of 12 stickers. If all of the stickers were distinct, there would be [latex]12![/latex] ways to order the stickers. However, 4 of the stickers are identical stars, and 3 are identical moons. Because all of the objects are not distinct, many of the [latex]12![/latex] permutations we counted are duplicates. The general formula for this situation is as follows.

[latex]\frac{n!}{{r}_{1}!{r}_{2}!\dots {r}_{k}!}[/latex]

In this example, we need to divide by the number of ways to order the 4 stars and the ways to order the 3 moons to find the number of unique permutations of the stickers. There are [latex]4![/latex] ways to order the stars and [latex]3![/latex] ways to order the moon.

[latex]\frac{12!}{4!3!}=3\text{,}326\text{,}400[/latex]

There are 3,326,400 ways to order the sheet of stickers.

A General Note: Formula for Finding the Number of Permutations of n Non-Distinct Objects

If there are [latex]n[/latex] elements in a set and [latex]{r}_{1}[/latex] are alike, [latex]{r}_{2}[/latex] are alike, [latex]{r}_{3}[/latex] are alike, and so on through [latex]{r}_{k}[/latex], the number of permutations can be found by

[latex]\frac{n!}{{r}_{1}!{r}_{2}!\dots {r}_{k}!}[/latex]

Example: Finding the Number of Permutations of n Non-Distinct Objects

Find the number of rearrangements of the letters in the word DISTINCT.

Answer: There are 8 letters. Both I and T are repeated 2 times. Substitute [latex]n=8, {r}_{1}=2, [/latex] and [latex] {r}_{2}=2 [/latex] into the formula.

[latex]\frac{8!}{2!2!}=10\text{,}080 [/latex]

There are 10,080 arrangements.

Try It

Find the number of rearrangements of the letters in the word CARRIER.

Answer: 840

Combinations

So far, we have looked at problems asking us to put objects in order. There are many problems in which we want to select a few objects from a group of objects, but we do not care about the order. When we are selecting objects and the order does not matter, we are dealing with combinations. A selection of [latex]r[/latex] objects from a set of [latex]n[/latex] objects where the order does not matter can be written as [latex]C\left(n,r\right)[/latex]. Just as with permutations, [latex]\text{C}\left(n,r\right)[/latex] can also be written as [latex]{}_{n}{C}_{r}[/latex]. In this case, the general formula is as follows.

[latex]\text{C}\left(n,r\right)=\frac{n!}{r!\left(n-r\right)!}[/latex]

An earlier problem considered choosing 3 of 4 possible paintings to hang on a wall. We found that there were 24 ways to select 3 of the 4 paintings in order. But what if we did not care about the order? We would expect a smaller number because selecting paintings 1, 2, 3 would be the same as selecting paintings 2, 3, 1. To find the number of ways to select 3 of the 4 paintings, disregarding the order of the paintings, divide the number of permutations by the number of ways to order 3 paintings. There are [latex]3!=3\cdot 2\cdot 1=6[/latex] ways to order 3 paintings. There are [latex]\frac{24}{6}[/latex], or 4 ways to select 3 of the 4 paintings. This number makes sense because every time we are selecting 3 paintings, we are not selecting 1 painting. There are 4 paintings we could choose not to select, so there are 4 ways to select 3 of the 4 paintings.

A General Note: Formula for Combinations of n Distinct Objects

Given [latex]n[/latex] distinct objects, the number of ways to select [latex]r[/latex] objects from the set is

[latex]\text{C}\left(n,r\right)=\frac{n!}{r!\left(n-r\right)!}[/latex]

How To: Given a number of options, determine the possible number of combinations.

  1. Identify [latex]n[/latex] from the given information.
  2. Identify [latex]r[/latex] from the given information.
  3. Replace [latex]n[/latex] and [latex]r[/latex] in the formula with the given values.
  4. Evaluate.

Example: Finding the Number of Combinations Using the Formula

A fast food restaurant offers five side dish options. Your meal comes with two side dishes.
  1. How many ways can you select your side dishes?
  2. How many ways can you select 3 side dishes?

Answer:

  1. We want to choose 2 side dishes from 5 options. [latex]\text{C}\left(5,2\right)=\frac{5!}{2!\left(5 - 2\right)!}=10[/latex]
  2. We want to choose 3 side dishes from 5 options. [latex]\text{C}\left(5,3\right)=\frac{5!}{3!\left(5 - 3\right)!}=10[/latex]

Analysis of the Solution

We can also use a graphing calculator to find combinations. Enter 5, then press [latex]{}_{n}{C}_{r}[/latex], enter 3, and then press the equal sign. The [latex]{}_{n}{C}_{r}[/latex], function may be located under the MATH menu with probability commands.

Q & A

Is it a coincidence that parts (a) and (b) in Example 4 have the same answers?

No. When we choose r objects from n objects, we are not choosing [latex]\left(n-r\right)[/latex] objects. Therefore, [latex]C\left(n,r\right)=C\left(n,n-r\right)[/latex].

Try It

An ice cream shop offers 10 flavors of ice cream. How many ways are there to choose 3 flavors for a banana split?

Answer: [latex]C\left(10,3\right)=120[/latex]

Finding the Number of Subsets of a Set

We have looked only at combination problems in which we chose exactly [latex]r[/latex] objects. In some problems, we want to consider choosing every possible number of objects. Consider, for example, a pizza restaurant that offers 5 toppings. Any number of toppings can be ordered. How many different pizzas are possible? To answer this question, we need to consider pizzas with any number of toppings. There is [latex]C\left(5,0\right)=1[/latex] way to order a pizza with no toppings. There are [latex]C\left(5,1\right)=5[/latex] ways to order a pizza with exactly one topping. If we continue this process, we get

[latex]C\left(5,0\right)+C\left(5,1\right)+C\left(5,2\right)+C\left(5,3\right)+C\left(5,4\right)+C\left(5,5\right)=32[/latex]

There are 32 possible pizzas. This result is equal to [latex]{2}^{5}[/latex]. We are presented with a sequence of choices. For each of the [latex]n[/latex] objects we have two choices: include it in the subset or not. So for the whole subset we have made [latex]n[/latex] choices, each with two options. So there are a total of [latex]2\cdot 2\cdot 2\cdot \dots \cdot 2[/latex] possible resulting subsets, all the way from the empty subset, which we obtain when we say "no" each time, to the original set itself, which we obtain when we say "yes" each time.

A General Note: Formula for the Number of Subsets of a Set

A set containing n distinct objects has [latex]{2}^{n}[/latex] subsets.

Example: Finding the Number of Subsets of a Set

A restaurant offers butter, cheese, chives, and sour cream as toppings for a baked potato. How many different ways are there to order a potato?

Answer: We are looking for the number of subsets of a set with 4 objects. Substitute [latex]n=4[/latex] into the formula.

[latex]\begin{array}{l}{2}^{n}={2}^{4}\hfill \\ \text{ }=16\hfill \end{array}[/latex]

There are 16 possible ways to order a potato.

Try It

A sundae bar at a wedding has 6 toppings to choose from. Any number of toppings can be chosen. How many different sundaes are possible?

Answer: 64 sundaes

Use the Binomial Theorem

Previously, we studied combinations. In the shortcut to finding [latex]{\left(x+y\right)}^{n}[/latex], we will need to use combinations to find the coefficients that will appear in the expansion of the binomial. In this case, we use the notation [latex]\left(\begin{array}{c}n\\ r\end{array}\right)[/latex] instead of [latex]C\left(n,r\right)[/latex], but it can be calculated in the same way. So

[latex]\left(\begin{array}{c}n\\ r\end{array}\right)=C\left(n,r\right)=\frac{n!}{r!\left(n-r\right)!}[/latex]

The combination [latex]\left(\begin{array}{c}n\\ r\end{array}\right)[/latex] is called a binomial coefficient. An example of a binomial coefficient is [latex]\left(\begin{array}{c}5\\ 2\end{array}\right)=C\left(5,2\right)=10[/latex].

A General Note: Binomial Coefficients

If [latex]n[/latex] and [latex]r[/latex] are integers greater than or equal to 0 with [latex]n\ge r[/latex], then the binomial coefficient is

[latex]\left(\begin{array}{c}n\\ r\end{array}\right)=C\left(n,r\right)=\frac{n!}{r!\left(n-r\right)!}

[/latex]

Q & A

Is a binomial coefficient always a whole number?

Yes. Just as the number of combinations must always be a whole number, a binomial coefficient will always be a whole number.

Example: Finding Binomial Coefficients

Find each binomial coefficient.
  1. [latex]\left(\begin{array}{c}5\\ 3\end{array}\right)[/latex]
  2. [latex]\left(\begin{array}{c}9\\ 2\end{array}\right)[/latex]
  3. [latex]\left(\begin{array}{c}9\\ 7\end{array}\right)[/latex]

Answer: Use the formula to calculate each binomial coefficient. You can also use the [latex]{n}_{}{C}_{r}[/latex] function on your calculator.

[latex]\left(\begin{array}{c}n\\ r\end{array}\right)=C\left(n,r\right)=\frac{n!}{r!\left(n-r\right)!}[/latex]

  1. [latex]\left(\begin{array}{c}5\\ 3\end{array}\right)=\frac{5!}{3!\left(5 - 3\right)!}=\frac{5\cdot 4\cdot 3!}{3!2!}=10[/latex]
  2. [latex]\left(\begin{array}{c}9\\ 2\end{array}\right)=\frac{9!}{2!\left(9 - 2\right)!}=\frac{9\cdot 8\cdot 7!}{2!7!}=36[/latex]
  3. [latex]\left(\begin{array}{c}9\\ 7\end{array}\right)=\frac{9!}{7!\left(9 - 7\right)!}=\frac{9\cdot 8\cdot 7!}{7!2!}=36[/latex]

Analysis of the Solution

Notice that we obtained the same result for parts (b) and (c). If you look closely at the solution for these two parts, you will see that you end up with the same two factorials in the denominator, but the order is reversed, just as with combinations.

[latex]\left(\begin{array}{c}n\\ r\end{array}\right)=\left(\begin{array}{c}n\\ n-r\end{array}\right)[/latex]

Try It

Find each binomial coefficient.
  1. [latex]\left(\begin{array}{c}7\\ 3\end{array}\right)[/latex]
  2. [latex]\left(\begin{array}{c}11\\ 4\end{array}\right)[/latex]

Answer:

  1. 35
  2. 330

When we expand [latex]{\left(x+y\right)}^{n}[/latex] by multiplying, the result is called a binomial expansion, and it includes binomial coefficients. If we wanted to expand [latex]{\left(x+y\right)}^{52}[/latex], we might multiply [latex]\left(x+y\right)[/latex] by itself fifty-two times. This could take hours! If we examine some simple binomial expansions, we can find patterns that will lead us to a shortcut for finding more complicated binomial expansions.

[latex]\begin{array}{l}{\left(x+y\right)}^{2}={x}^{2}+2xy+{y}^{2}\hfill \\ {\left(x+y\right)}^{3}={x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3}\hfill \\ {\left(x+y\right)}^{4}={x}^{4}+4{x}^{3}y+6{x}^{2}{y}^{2}+4x{y}^{3}+{y}^{4}\hfill \end{array}[/latex]

First, let’s examine the exponents. With each successive term, the exponent for [latex]x[/latex] decreases and the exponent for [latex]y[/latex] increases. The sum of the two exponents is [latex]n[/latex] for each term. Next, let’s examine the coefficients. Notice that the coefficients increase and then decrease in a symmetrical pattern. The coefficients follow a pattern:

[latex]\left(\begin{array}{c}n\\ 0\end{array}\right),\left(\begin{array}{c}n\\ 1\end{array}\right),\left(\begin{array}{c}n\\ 2\end{array}\right),...,\left(\begin{array}{c}n\\ n\end{array}\right)[/latex].

These patterns lead us to the Binomial Theorem, which can be used to expand any binomial.

[latex]\begin{array}{ll}{\left(x+y\right)}^{n}\hfill & =\sum _{k=0}^{n}\left(\begin{array}{c}n\\ k\end{array}\right){x}^{n-k}{y}^{k}\hfill \\ \hfill & ={x}^{n}+\left(\begin{array}{c}n\\ 1\end{array}\right){x}^{n - 1}y+\left(\begin{array}{c}n\\ 2\end{array}\right){x}^{n - 2}{y}^{2}+...+\left(\begin{array}{c}n\\ n - 1\end{array}\right)x{y}^{n - 1}+{y}^{n}\hfill \end{array}[/latex]

Another way to see the coefficients is to examine the expansion of a binomial in general form, [latex]x+y[/latex], to successive powers 1, 2, 3, and 4.

[latex]\begin{array}{l}{\left(x+y\right)}^{1}=x+y\hfill \\ {\left(x+y\right)}^{2}={x}^{2}+2xy+{y}^{2}\hfill \\ {\left(x+y\right)}^{3}={x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3}\hfill \\ {\left(x+y\right)}^{4}={x}^{4}+4{x}^{3}y+6{x}^{2}{y}^{2}+4x{y}^{3}+{y}^{4}\hfill \end{array}[/latex]

Can you guess the next expansion for the binomial [latex]{\left(x+y\right)}^{5}?[/latex] Graph of the function f_2. Above is an illustration the following:
  • There are [latex]n+1[/latex] terms in the expansion of [latex]{\left(x+y\right)}^{n}[/latex].
  • The degree (or sum of the exponents) for each term is [latex]n[/latex].
  • The powers on [latex]x[/latex] begin with [latex]n[/latex] and decrease to 0.
  • The powers on [latex]y[/latex] begin with 0 and increase to [latex]n[/latex].
  • The coefficients are symmetric.
To determine the expansion on [latex]{\left(x+y\right)}^{5}[/latex], we see [latex]n=5[/latex], thus, there will be 5+1 = 6 terms. Each term has a combined degree of 5. In descending order for powers of [latex]x[/latex], the pattern is as follows:
  • Introduce [latex]{x}^{5}[/latex], and then for each successive term reduce the exponent on [latex]x[/latex] by 1 until [latex]{x}^{0}=1[/latex] is reached.
  • Introduce [latex]{y}^{0}=1[/latex], and then increase the exponent on [latex]y[/latex] by 1 until [latex]{y}^{5}[/latex] is reached. [latex]{x}^{5},{x}^{4}y,{x}^{3}{y}^{2},{x}^{2}{y}^{3},x{y}^{4},{y}^{5}[/latex]
The next expansion would be

[latex]{\left(x+y\right)}^{5}={x}^{5}+5{x}^{4}y+10{x}^{3}{y}^{2}+10{x}^{2}{y}^{3}+5x{y}^{4}+{y}^{5}[/latex].

But where do those coefficients come from? The binomial coefficients are symmetric. We can see these coefficients in an array known as Pascal's Triangle.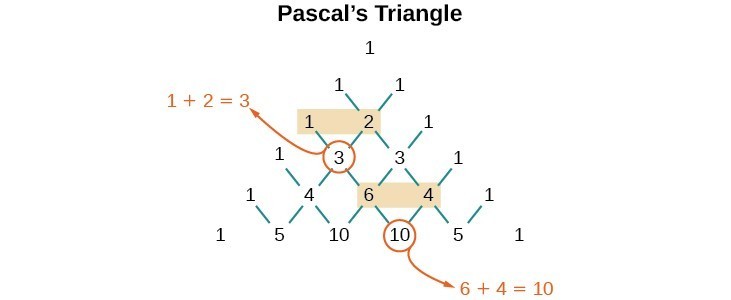 Pascal's Triangle To generate Pascal’s Triangle, we start by writing a 1. In the row below, row 2, we write two 1’s. In the 3rd row, flank the ends of the rows with 1’s, and add [latex]1+1[/latex] to find the middle number, 2. In the [latex]n\text{th}[/latex] row, flank the ends of the row with 1’s. Each element in the triangle is the sum of the two elements immediately above it. To see the connection between Pascal’s Triangle and binomial coefficients, let us revisit the expansion of the binomials in general form. 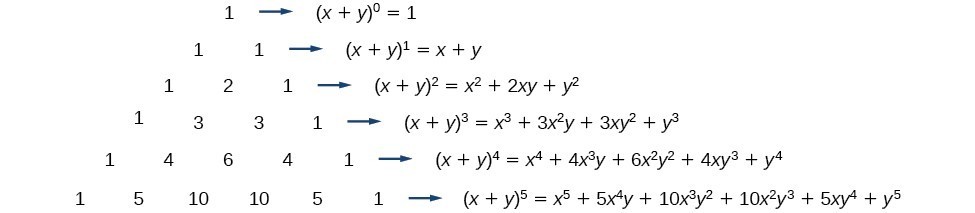Pascal's Triangle expanded to show the values of the triangle as x and y terms with exponents

A General Note: The Binomial Theorem

The Binomial Theorem is a formula that can be used to expand any binomial.

[latex]\begin{array}{ll}{\left(x+y\right)}^{n}\hfill & =\sum _{k=0}^{n}\left(\begin{array}{c}n\\ k\end{array}\right){x}^{n-k}{y}^{k}\hfill \\ \hfill & ={x}^{n}+\left(\begin{array}{c}n\\ 1\end{array}\right){x}^{n - 1}y+\left(\begin{array}{c}n\\ 2\end{array}\right){x}^{n - 2}{y}^{2}+...+\left(\begin{array}{c}n\\ n - 1\end{array}\right)x{y}^{n - 1}+{y}^{n}\hfill \end{array}[/latex]

How To: Given a binomial, write it in expanded form.

  1. Determine the value of [latex]n[/latex] according to the exponent.
  2. Evaluate the [latex]k=0[/latex] through [latex]k=n[/latex] using the Binomial Theorem formula.
  3. Simplify.

Example: Expanding a Binomial

Write in expanded form.
  1. [latex]{\left(x+y\right)}^{5}[/latex]
  2. [latex]{\left(3x-y\right)}^{4}[/latex]

Answer:

  1. Substitute [latex]n=5[/latex] into the formula. Evaluate the [latex]k=0[/latex] through [latex]k=5[/latex] terms. Simplify.
    [latex-display]\begin{array}{ll}{\left(x+y\right)}^{5}\hfill & =\left(\begin{array}{c}5\\ 0\end{array}\right){x}^{5}{y}^{0}+\left(\begin{array}{c}5\\ 1\end{array}\right){x}^{4}{y}^{1}+\left(\begin{array}{c}5\\ 2\end{array}\right){x}^{3}{y}^{2}+\left(\begin{array}{c}5\\ 3\end{array}\right){x}^{2}{y}^{3}+\left(\begin{array}{c}5\\ 4\end{array}\right){x}^{1}{y}^{4}+\left(\begin{array}{c}5\\ 5\end{array}\right){x}^{0}{y}^{5}\hfill \\ {\left(x+y\right)}^{5}\hfill & ={x}^{5}+5{x}^{4}y+10{x}^{3}{y}^{2}+10{x}^{2}{y}^{3}+5x{y}^{4}+{y}^{5}\hfill \end{array}[/latex-display]
  2. Substitute [latex]n=4[/latex] into the formula. Evaluate the [latex]k=0[/latex] through [latex]k=4[/latex] terms. Notice that [latex]3x[/latex] is in the place that was occupied by [latex]x[/latex] and that [latex]-y[/latex] is in the place that was occupied by [latex]y[/latex]. So we substitute them. Simplify.
    [latex]\begin{array}{ll}{\left(3x-y\right)}^{4}\hfill & =\left(\begin{array}{c}4\\ 0\end{array}\right){\left(3x\right)}^{4}{\left(-y\right)}^{0}+\left(\begin{array}{c}4\\ 1\end{array}\right){\left(3x\right)}^{3}{\left(-y\right)}^{1}+\left(\begin{array}{c}4\\ 2\end{array}\right){\left(3x\right)}^{2}{\left(-y\right)}^{2}+\left(\begin{array}{c}4\\ 3\end{array}\right){\left(3x\right)}^{1}{\left(-y\right)}^{3}+\left(\begin{array}{c}4\\ 4\end{array}\right){\left(3x\right)}^{0}{\left(-y\right)}^{4}\hfill \\ {\left(3x-y\right)}^{4}\hfill & =81{x}^{4}-108{x}^{3}y+54{x}^{2}{y}^{2}-12x{y}^{3}+{y}^{4}\hfill \end{array}[/latex]

Analysis of the Solution

Notice the alternating signs in part b. This happens because [latex]\left(-y\right)[/latex] raised to odd powers is negative, but [latex]\left(-y\right)[/latex] raised to even powers is positive. This will occur whenever the binomial contains a subtraction sign.

Try It

Write in expanded form.
  1. [latex]{\left(x-y\right)}^{5}[/latex]
  2. [latex]{\left(2x+5y\right)}^{3}[/latex]

Answer:

  1. [latex]{x}^{5}-5{x}^{4}y+10{x}^{3}{y}^{2}-10{x}^{2}{y}^{3}+5x{y}^{4}-{y}^{5}[/latex]
  2. [latex]8{x}^{3}+60{x}^{2}y+150x{y}^{2}+125{y}^{3}[/latex]

Using the Binomial Theorem to Find a Single Term

Expanding a binomial with a high exponent such as [latex]{\left(x+2y\right)}^{16}[/latex] can be a lengthy process. Sometimes we are interested only in a certain term of a binomial expansion. We do not need to fully expand a binomial to find a single specific term. Note the pattern of coefficients in the expansion of [latex]{\left(x+y\right)}^{5}[/latex].

[latex]{\left(x+y\right)}^{5}={x}^{5}+\left(\begin{array}{c}5\\ 1\end{array}\right){x}^{4}y+\left(\begin{array}{c}5\\ 2\end{array}\right){x}^{3}{y}^{2}+\left(\begin{array}{c}5\\ 3\end{array}\right){x}^{2}{y}^{3}+\left(\begin{array}{c}5\\ 4\end{array}\right)x{y}^{4}+{y}^{5}[/latex]

The second term is [latex]\left(\begin{array}{c}5\\ 1\end{array}\right){x}^{4}y[/latex]. The third term is [latex]\left(\begin{array}{c}5\\ 2\end{array}\right){x}^{3}{y}^{2}[/latex]. We can generalize this result.

[latex]\left(\begin{array}{c}n\\ r\end{array}\right){x}^{n-r}{y}^{r}[/latex]

A General Note: The (r+1)th Term of a Binomial Expansion

The [latex]\left(r+1\right)\text{th}[/latex] term of the binomial expansion of [latex]{\left(x+y\right)}^{n}[/latex] is:

[latex]\left(\begin{array}{c}n\\ r\end{array}\right){x}^{n-r}{y}^{r}[/latex]

How To: Given a binomial, write a specific term without fully expanding.

  1. Determine the value of [latex]n[/latex] according to the exponent.
  2. Determine [latex]\left(r+1\right)[/latex].
  3. Determine [latex]r[/latex].
  4. Replace [latex]r[/latex] in the formula for the [latex]\left(r+1\right)\text{th}[/latex] term of the binomial expansion.

Example: Writing a Given Term of a Binomial Expansion

Find the tenth term of [latex]{\left(x+2y\right)}^{16}[/latex] without fully expanding the binomial.

Answer: Because we are looking for the tenth term, [latex]r+1=10[/latex], we will use [latex]r=9[/latex] in our calculations.

[latex]\left(\begin{array}{c}n\\ r\end{array}\right){x}^{n-r}{y}^{r}[/latex]

[latex]\left(\begin{array}{c}16\\ 9\end{array}\right){x}^{16 - 9}{\left(2y\right)}^{9}=5\text{,}857\text{,}280{x}^{7}{y}^{9}[/latex]

Try It

Find the sixth term of [latex]{\left(3x-y\right)}^{9}[/latex] without fully expanding the binomial.

Answer: [latex]-10,206{x}^{4}{y}^{5}[/latex]

Key Equations

number of permutations of [latex]n[/latex] distinct objects taken [latex]r[/latex] at a time [latex]P\left(n,r\right)=\frac{n!}{\left(n-r\right)!}[/latex]
number of combinations of [latex]n[/latex] distinct objects taken [latex]r[/latex] at a time [latex]C\left(n,r\right)=\frac{n!}{r!\left(n-r\right)!}[/latex]
number of permutations of [latex]n[/latex] non-distinct objects [latex]\frac{n!}{{r}_{1}!{r}_{2}!\dots {r}_{k}!}[/latex]
Binomial Theorem [latex]{\left(x+y\right)}^{n}=\sum _{k - 0}^{n}\left(\begin{array}{c}n\\ k\end{array}\right){x}^{n-k}{y}^{k}[/latex]
[latex]\left(r+1\right)th[/latex] term of a binomial expansion [latex]\left(\begin{array}{c}n\\ r\end{array}\right){x}^{n-r}{y}^{r}[/latex]

Key Concepts

  • If one event can occur in [latex]m[/latex] ways and a second event with no common outcomes can occur in [latex]n[/latex] ways, then the first or second event can occur in [latex]m+n[/latex] ways.
  • If one event can occur in [latex]m[/latex] ways and a second event can occur in [latex]n[/latex] ways after the first event has occurred, then the two events can occur in [latex]m\times n[/latex] ways.
  • A permutation is an ordering of [latex]n[/latex] objects.
  • If we have a set of [latex]n[/latex] objects and we want to choose [latex]r[/latex] objects from the set in order, we write [latex]P\left(n,r\right)[/latex].
  • Permutation problems can be solved using the Multiplication Principle or the formula for [latex]P\left(n,r\right)[/latex].
  • A selection of objects where the order does not matter is a combination.
  • Given [latex]n[/latex] distinct objects, the number of ways to select [latex]r[/latex] objects from the set is [latex]\text{C}\left(n,r\right)[/latex] and can be found using a formula.
  • A set containing [latex]n[/latex] distinct objects has [latex]{2}^{n}[/latex] subsets.
  • For counting problems involving non-distinct objects, we need to divide to avoid counting duplicate permutations.
  • [latex]\left(\begin{array}{c}n\\ r\end{array}\right)[/latex] is called a binomial coefficient and is equal to [latex]C\left(n,r\right)[/latex].
  • The Binomial Theorem allows us to expand binomials without multiplying.
  • We can find a given term of a binomial expansion without fully expanding the binomial.

Glossary

Addition Principle if one event can occur in [latex]m[/latex] ways and a second event with no common outcomes can occur in [latex]n[/latex] ways, then the first or second event can occur in [latex]m+n[/latex] ways binomial coefficient the number of ways to choose r objects from n objects where order does not matter; equivalent to [latex]C\left(n,r\right)[/latex], denoted [latex]\left(\begin{array}{c}n\\ r\end{array}\right)[/latex] binomial expansion the result of expanding [latex]{\left(x+y\right)}^{n}[/latex] by multiplying Binomial Theorem a formula that can be used to expand any binomial combination a selection of objects in which order does not matter Fundamental Counting Principle if one event can occur in [latex]m[/latex] ways and a second event can occur in [latex]n[/latex] ways after the first event has occurred, then the two events can occur in [latex]m\times n[/latex] ways; also known as the Multiplication Principle Multiplication Principle if one event can occur in [latex]m[/latex] ways and a second event can occur in [latex]n[/latex] ways after the first event has occurred, then the two events can occur in [latex]m\times n[/latex] ways; also known as the Fundamental Counting Principle permutation a selection of objects in which order matters

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 7155. Authored by: unknown, mb Lippman,David, mb Sousa,James. License: CC BY: Attribution. License terms: IMathAS Community LicenseCC-BY + GPL.
  • Question ID 7164. Authored by: WebWork-Rochester. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 32832. Authored by: David Lippman. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Ex: Determine the Number of Ways 6 Books can be Selected from 9 Books (Combination). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Question ID 7175, 7156. Authored by: unknown, mb Lippman,David, mb Sousa,James. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 18745. Authored by: Shahbazian, Roy. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.

CC licensed content, Specific attribution