We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra: Co-requisite Course

Algebraic Operations on Polynomials

Learning Objectives

  • Anatomy of a polynomial
    • Identify the degree and leading coefficient of a polynomial
    • Evaluate a polynomial for given values
  • Sums and Products of Polynomials
    • Add and subtract polynomials
    • Find the product of polynomials
    • Find the product of two binomials using the FOIL method
  • Multiply a Trinomial and a Binomial

Anatomy of a Polynomial

In the example on the previous page, we saw how combining the formulas for different shapes provides a way to accurately predict the amount of paint needed for a construction project. The result was a polynomial. A polynomial function is a function consisting of sum or difference of terms in which each term is a real number, a variable, or the product of a real number and variables with an non-negative integer exponents. Non negative integers are 0, 1, 2, 3, 4, ... You may see a resemblance between expressions and polynomials, which we have been studying in this course.  Polynomials are a special sub-group of mathematical expressions and equations. The following table is intended to help you tell the difference between what is a polynomial and what is not.
IS a Polynomial Is NOT a Polynomial Because
[latex]2x^2-\frac{1}{2}x -9[/latex] [latex]\frac{2}{x^{2}}+x[/latex] Polynomials only have variables in the numerator
[latex]\frac{y}{4}-y^3[/latex] [latex]\frac{2}{y}+4[/latex] Polynomials only have variables in the numerator
[latex]\sqrt{12}\left(a\right)+9[/latex]  [latex]\sqrt{a}+7[/latex] Roots are equivalent to rational exponents, and polynomials only have integer exponents
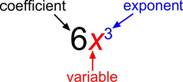The basic building block of a polynomial is a monomial. A monomial is one term and can be a number, a variable, or the product of a number and variables with an exponent. The number part of the term is called the coefficient. The expression 6x to the power of 3. 6 is the coefficient, x is the variable, and the power of 3 is the exponent. A polynomial containing two terms, such as [latex]2x - 9[/latex], is called a binomial. A polynomial containing three terms, such as [latex]-3{x}^{2}+8x - 7[/latex], is called a trinomial. We can find the degree of a polynomial by identifying the highest power of the variable that occurs in the polynomial. The term with the highest degree is called the leading term because it is usually written first. The coefficient of the leading term is called the leading coefficient. When a polynomial is written so that the powers are descending, we say that it is in standard form. It is important to note that polynomials only have integer exponents. 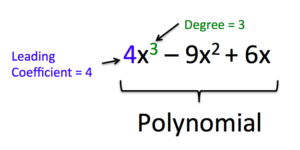4x^3 - 9x^2 + 6x, with the text

Given a polynomial expression, identify the degree and leading coefficient.

  1. Find the highest power of x to determine the degree.
  2. Identify the term containing the highest power of x to find the leading term.
  3. Identify the coefficient of the leading term.

Example

For the following polynomials, identify the degree, the leading term, and the leading coefficient.
  1. [latex]3+2{x}^{2}-4{x}^{3}[/latex]
  2. [latex]5{t}^{5}-2{t}^{3}+7t[/latex]
  3. [latex]6p-{p}^{3}-2[/latex]

Answer:

  1. The highest power of x is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-4{x}^{3}[/latex]. The leading coefficient is the coefficient of that term, [latex]-4[/latex].
  2. The highest power of t is [latex]5[/latex], so the degree is [latex]5[/latex]. The leading term is the term containing that degree, [latex]5{t}^{5}[/latex]. The leading coefficient is the coefficient of that term, [latex]5[/latex].
  3. The highest power of p is [latex]3[/latex], so the degree is [latex]3[/latex]. The leading term is the term containing that degree, [latex]-{p}^{3}[/latex], The leading coefficient is the coefficient of that term, [latex]-1[/latex].

  In the following video example, we will identify the terms, leading coefficient, and degree of a polynomial. https://youtu.be/3u16B2PN9zk The table below illustrates some examples of monomials, binomials, trinomials, and other polynomials. They are all written in standard form.
Monomials Binomials Trinomials Other Polynomials
15 [latex]3y+13[/latex] [latex]x^{3}-x^{2}+1[/latex] [latex]5x^{4}+3x^{3}-6x^{2}+2x[/latex]
[latex] \displaystyle \frac{1}{2}x[/latex] [latex]4p-7[/latex] [latex]3x^{2}+2x-9[/latex] [latex]\frac{1}{3}x^{5}-2x^{4}+\frac{2}{9}x^{3}-x^{2}+4x-\frac{5}{6}[/latex]
[latex]-4y^{3}[/latex] [latex]3x^{2}+\frac{5}{8}x[/latex] [latex]3y^{3}+y^{2}-2[/latex] [latex]3t^{3}-3t^{2}-3t-3[/latex]
[latex]16n^{4}[/latex] [latex]14y^{3}+3y[/latex] [latex]a^{7}+2a^{5}-3a^{3}[/latex] [latex]q^{7}+2q^{5}-3q^{3}+q[/latex]
When the coefficient of a polynomial term is 0, you usually do not write the term at all (because 0 times anything is 0, and adding 0 doesn’t change the value). The last binomial above could be written as a trinomial, [latex]14y^{3}+0y^{2}+3y[/latex]. A term without a variable is called a constant term, and the degree of that term is 0. For example 13 is the constant term in [latex]3y+13[/latex]. You would usually say that [latex]14y^{3}+3y[/latex] has no constant term or that the constant term is 0.

Evaluate a polynomial

You can evaluate polynomials just as you have been evaluating expressions all along. To evaluate an expression for a value of the variable, you substitute the value for the variable every time it appears. Then use the order of operations to find the resulting value for the expression.

Example

Evaluate [latex]3x^{2}-2x+1[/latex] for [latex]x=-1[/latex].

Answer: Substitute [latex]-1[/latex] for each x in the polynomial.

[latex]3\left(-1\right)^{2}-2\left(-1\right)+1[/latex]

Following the order of operations, evaluate exponents first.

[latex]3\left(1\right)-2\left(-1\right)+1[/latex]

Multiply 3 times 1, and then multiply [latex]-2[/latex] times [latex]-1[/latex].

[latex]3+\left(-2\right)\left(-1\right)+1[/latex]

Change the subtraction to addition of the opposite.

[latex]3+2+1[/latex]

Find the sum.

Answer

[latex-display]3x^{2}-2x+1=6[/latex], for [latex]x=-1[/latex-display]

Example

Evaluate [latex] \displaystyle -\frac{2}{3}p^{4}+2^{3}-p[/latex] for [latex]p = 3[/latex].

Answer: Substitute 3 for each p in the polynomial.

[latex] \displaystyle -\frac{2}{3}\left(3\right)^{4}+2\left(3\right)^{3}-3[/latex]

Following the order of operations, evaluate exponents first and then multiply.

[latex] \displaystyle -\frac{2}{3}\left(81\right)+2\left(27\right)-3[/latex]

Add and then subtract to get [latex]-3[/latex].

[latex]-54 + 54 – 3[/latex]

Answer

[latex-display] \displaystyle -\frac{2}{3}p^{4}+2p^{3}-p=-3[/latex], for [latex]p = 3[/latex-display]

 IN the following video we show more examples of evaluating polynomials for given values of the variable.

https://youtu.be/2EeFrgQP1hM

Add and Subtract Polynomials

We can add and subtract polynomials by combining like terms, which are terms that contain the same variables raised to the same exponents. For example, [latex]5{x}^{2}[/latex] and [latex]-2{x}^{2}[/latex] are like terms, and can be added to get [latex]3{x}^{2}[/latex], but [latex]3x[/latex] and [latex]3{x}^{2}[/latex] are not like terms, and therefore cannot be added.

Example

Find the sum.

[latex]\left(12{x}^{2}+9x - 21\right)+\left(4{x}^{3}+8{x}^{2}-5x+20\right)[/latex]

Answer:

[latex]\begin{array}{cc}4{x}^{3}+\left(12{x}^{2}+8{x}^{2}\right)+\left(9x - 5x\right)+\left(-21+20\right) \hfill & \text{Combine like terms}.\hfill \\ 4{x}^{3}+20{x}^{2}+4x - 1\hfill & \text{Simplify}.\hfill \end{array}[/latex]

Here is a summary of some helpful steps for adding and subtracting polynomials.

 Given multiple polynomials, add or subtract them to simplify the expressions.

  1. Combine like terms.
  2. Simplify and write in standard form.
When you subtract polynomials you will still be looking for like terms to combine, but you will need to pay attention to the sign of the terms you are combining. In the following example we will show how to distribute the negative sign to each term of a polynomial that is being subtracted from another.

Example

Find the difference.

[latex]\left(7{x}^{4}-{x}^{2}+6x+1\right)-\left(5{x}^{3}-2{x}^{2}+3x+2\right)[/latex]

Answer:

[latex]\begin{array}{cc}7{x}^{4}-5{x}^{3}+\left(-{x}^{2}+2{x}^{2}\right)+\left(6x - 3x\right)+\left(1 - 2\right)\text{ }\hfill & \text{Combine like terms}.\hfill \\ 7{x}^{4}-5{x}^{3}+{x}^{2}+3x - 1\hfill & \text{Simplify}.\hfill \end{array}[/latex]

Analysis of the Solution

Note that finding the difference between two polynomials is the same as adding the opposite of the second polynomial to the first. In the following video we show more examples of adding and subtracting polynomials. https://youtu.be/jiq3toC7wGM

Multiplying Polynomials

Multiplying polynomials is a bit more challenging than adding and subtracting polynomials. We must use the distributive property to multiply each term in the first polynomial by each term in the second polynomial. We then combine like terms. You may have used the distributive property to help you solve linear equations such as [latex]2\left(x+7\right)=21[/latex]. We can distribute the [latex]2[/latex] in [latex]2\left(x+7\right)[/latex] to obtain the equivalent expression [latex]2x+14[/latex]. When multiplying polynomials, the distributive property allows us to multiply each term of the first polynomial by each term of the second. We then add the products together and combine like terms to simplify. The following video will provide you with examples of using the distributive property to find the product of monomials and polynomials. https://youtu.be/bwTmApTV_8o Below is a summary of the steps we used to find the product of two polynomials using the distributive property.

How To: Given the multiplication of two polynomials, use the distributive property to simplify the expression.

  1. Multiply each term of the first polynomial by each term of the second.
  2. Combine like terms.
  3. Simplify.

Using FOIL to Multiply Binomials

We can also use a shortcut called the FOIL method when multiplying binomials. It is called FOIL because we multiply the first terms, the outer terms, the inner terms, and then the last terms of each binomial. Two quantities in parentheses are being multiplied, the first being: a times x plus b and the second being: c times x plus d. This expression equals ac times x squared plus ad times x plus bc times x plus bd. The terms ax and cx are labeled: First Terms. The terms ax and d are labeled: Outer Terms. The terms b and cx are labeled: Inner Terms. The terms b and d are labeled: Last Terms. The FOIL method arises out of the distributive property. We are simply multiplying each term of the first binomial by each term of the second binomial, and then combining like terms.

Example

Use FOIL to find the product. [latex](2x-18)(3x+3)[/latex]

Answer: Find the product of the first terms. Find the product of the outer terms. Find the product of the inner terms. Find the product of the last terms.

[latex]\begin{array}{cc}6{x}^{2}+6x - 54x - 54\hfill & \text{Add the products}.\hfill \\ 6{x}^{2}+\left(6x - 54x\right)-54\hfill & \text{Combine like terms}.\hfill \\ 6{x}^{2}-48x - 54\hfill & \text{Simplify}.\hfill \end{array}[/latex]

In this video, we show an example of how to use the FOIL method to multiply two binomials. https://youtu.be/_MrdEFnXNGA The following steps summarize the process for using FOIL to multiply two binomials.  It is very important to note that this process only works for the product of two binomials. If you are multiplying a binomial and a trinomial, it is better to use a table to keep track of your terms.

How To: Given two binomials, use FOIL to simplify the expression.

  1. Multiply the first terms of each binomial.
  2. Multiply the outer terms of the binomials.
  3. Multiply the inner terms of the binomials.
  4. Multiply the last terms of each binomial.
  5. Add the products.
  6. Combine like terms and simplify.

Multiply a Trinomial and a Binomial

Another type of polynomial multiplication problem is the product of a binomial and trinomial. Although the FOIL method can not be used since there are more than two terms in a trinomial, you still use the Distributive Property to organize the individual products. Using the distributive property, each term in the binomial must be multiplied by each of the terms in the trinomial. For our first examples, we will show you two ways to organize all of the terms that result from multiplying polynomials with more than two terms. The most important part of the process is finding a way to organize terms.

Example

Find the product.  [latex]\left(3x+6\right)\left(5x^{2}+3x+10\right)[/latex].

Answer: Distribute the trinomial to each term in the binomial. [latex-display]3x\left(5x^{2}+3x+10\right)+6\left(5x2+3x+10\right)[/latex-display] Use the distributive property to distribute the monomials to each term in the trinomials. [latex-display]3x\left(5x^{2}\right)+3x\left(3x\right)+3x\left(10\right)+6\left(5x^{2}\right)+6\left(3x\right)+6\left(10\right)[/latex-display] Multiply. [latex-display]15x^{3}9x^{2}+30x^{2}+18x+60[/latex-display] Group like terms. [latex-display]15x^{3}+\left(9x^{2}+30x^{2}\right)+\left(30x+18x\right)+60[/latex-display] Combine like terms.

Answer

[latex-display]\left(3x+6\right)\left(5x^{2}+3x+10\right)=15x^{3}+39x^{2}+48x+60[/latex-display]

As you can see, multiplying a binomial by a trinomial leads to a lot of individual terms! Using the same problem as above, we will show another way to organize all the terms produced by multiplying two polynomials with more than two terms.

Example

Multiply. [latex]\left(3x+6\right)\left(5x^{2}+3x+10\right)[/latex]

Answer: Set up the problem in a vertical form, and begin by multiplying [latex]3x+6[/latex] by [latex]+10[/latex]. Place the products underneath, as shown. [latex-display]\begin{array}{r}3x+\,\,\,6\,\\\underline{\times\,\,\,\,\,\,5x^{2}+\,\,3x+10}\\+30x+60\,\end{array}[/latex-display] Now multiply [latex]3x+6[/latex] by [latex]+3x[/latex]. Notice that [latex]\left(6\right)\left(3x\right)=18x[/latex]; since this term is like [latex]30x[/latex], place it directly beneath it. [latex-display]\begin{array}{r}3x\,\,\,\,\,\,+\,\,\,6\,\,\\\underline{\times\,\,\,\,\,\,5x^{2}\,\,\,\,\,\,+3x\,\,\,\,\,\,+10}\\+30x\,\,\,\,\,+60\,\,\\+9x^{2}\,\,\,+18x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex-display] Finally, multiply [latex]3x+6[/latex] by [latex]5x^{2}[/latex]. Notice that [latex]30x^{2}[/latex] is placed underneath [latex]9x^{2}[/latex]. [latex-display]\begin{array}{r}3x\,\,\,\,\,\,+\,\,\,6\,\,\\\underline{\times\,\,\,\,\,\,5x^{2}\,\,\,\,\,\,+3x\,\,\,\,\,\,+10}\\+30x\,\,\,\,\,+60\,\,\\+9x^{2}\,\,\,+18x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\underline{+15x^{3}+30x^{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}[/latex-display] Now add like terms. [latex-display]\begin{array}{r}3x\,\,\,\,\,\,+\,\,\,6\,\,\\\underline{\times\,\,\,\,\,\,5x^{2}\,\,\,\,\,\,+3x\,\,\,\,\,\,+10}\\+30x\,\,\,\,\,+60\,\,\\+9x^{2}\,\,\,+18x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\underline{+15x^{3}\,\,\,\,\,\,+30x^{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\+15x^{3}\,\,\,\,\,\,+39x^{2}\,\,\,\,+48x\,\,\,\,\,+60\end{array}[/latex-display]

Answer

[latex-display]15x^{3}+39x^{2}+48x+60[/latex-display]

Notice that although the two problems were solved using different strategies, the product is the same. Both the horizontal and vertical methods apply the Distributive Property to multiply a binomial by a trinomial. In our next example we will multiply a binomial and a trinomial that contains subtraction. Pay attention to the signs on the terms.  Forgetting a negative sign is the easiest mistake to make in this case.

Example

Find the product. [latex-display]\left(2x+1\right)\left(3{x}^{2}-x+4\right)[/latex-display]

Answer: [latex-display]\begin{array}{cc}2x\left(3{x}^{2}-x+4\right)+1\left(3{x}^{2}-x+4\right) \hfill & \text{Use the distributive property}.\hfill \\ \left(6{x}^{3}-2{x}^{2}+8x\right)+\left(3{x}^{2}-x+4\right)\hfill & \text{Multiply}.\hfill \\ 6{x}^{3}+\left(-2{x}^{2}+3{x}^{2}\right)+\left(8x-x\right)+4\hfill & \text{Combine like terms}.\hfill \\ 6{x}^{3}+{x}^{2}+7x+4 \hfill & \text{Simplify}.\hfill \end{array}[/latex-display]

Analysis of the Solution

Another way to keep track of all the terms involved in this product is to use a table, as shown below. Write one polynomial across the top and the other down the side. For each box in the table, multiply the term for that row by the term for that column. Then add all of the terms together, combine like terms, and simplify. Notice how we kept the sign on each term, for example we are subtracting [latex]x[/latex] from [latex]3x^2[/latex], so we place [latex]-x[/latex] in the table.
[latex]3{x}^{2}[/latex] [latex]-x[/latex] [latex]+4[/latex]
[latex]2x[/latex] [latex]6{x}^{3}\\[/latex] [latex]-2{x}^{2}[/latex] [latex]8x[/latex]
[latex]+1[/latex] [latex]3{x}^{2}[/latex] [latex]-x[/latex] [latex]4[/latex]

Example

Multiply.  [latex]\left(2p-1\right)\left(3p^{2}-3p+1\right)[/latex]

Answer: Distribute 2p and -1 to each term in the trinomial.

[latex]2p\left(3p^{2}-3p+1\right)-1\left(3p^{2}-3p+1\right)[/latex]

[latex]2p\left(3p^{2}\right)+2p\left(-3p\right)+2p\left(1\right)-1\left(3p^{2}\right)-1\left(-3p\right)-1\left(1\right)[/latex]

Multiply. (Notice that the subtracted 1 and the subtracted 3p have a positive product that is added.)

[latex]6p^{3}-6p^{2}+2p-3p^{2}+3p-1[/latex]

Combine like terms.

[latex]6p^{3}-9p^{2}+5p-1[/latex]

Answer

[latex-display]6p^{3}-9p^{2}+5p-1[/latex-display]

In the following video we show more examples of multiplying polynomials. https://youtu.be/bBKbldmlbqI  

Licenses & Attributions

CC licensed content, Original

  • Evaluate a Polynomial in One Variable. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
  • Ex: Multiplying Using the Distributive Property. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Multiply Binomials Using An Area Model and Using Repeated Distribution. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Multiply Binomials Using the FOIL Acronym. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Divide a Degree 3 Polynomial by a Degree 1 Polynomial (Long Division with Missing Term). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Screenshot Polynomial Generated Images. Provided by: Lumen Learning License: CC BY: Attribution.

CC licensed content, Shared previously

  • Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
  • College Algebra. Authored by: Abramson, Jay, et al.. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: Public Domain: No Known Copyright. License terms: Download for free at :http://cnx.org/contents/[email protected]:1/Preface.
  • Ex: Intro to Polynomials in One Variable. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex: Adding and Subtracting Polynomials. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Ex: Polynomial Multiplication Involving Binomials and Trinomials. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex 1: Divide a Trinomial by a Binomial Using Long Division. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Ex 6: Divide a Polynomial by a Degree Two Binomial Using Long Division. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex 1: Divide a Trinomial by a Binomial Using Synthetic Division. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex 3: Divide a Polynomial by a Binomial Using Synthetic Division. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.