We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra: Co-requisite Course

Function Notation

Learning Objectives

  • Define a function using tables
  • Define a function from a set of ordered pairs
  • Define the domain and range of a function given as a table or a set of ordered pairs
  • Write functions using algebraic notation
  • Use the vertical line test to determine whether a graph represents a function
  • Graphs of functions
  • Variable inputs
Algebra gives us a way to explore and describe relationships. Imagine tossing a ball straight up in the air and watching it rise to reach its highest point before dropping back down into your hands. As time passes, the height of the ball changes. There is a relationship between the amount of time that has elapsed since the toss and the height of the ball. In mathematics, a correspondence between variables that change together (such as time and height) is called a relation. Some, but not all, relations can also be described as functions. There are many kinds of relations. Relations are simply correspondences between sets of values or information. Think about members of your family and their ages. The pairing of each member of your family and their age is a relation. Each family member can be paired with an age in the set of ages of your family members. Another example of a relation is the pairing of a state with its United States’ senators. Each state can be matched with two individuals who have been elected to serve as senator. In turn, each senator can be matched with one specific state that he or she represents. Both of these are real-life examples of relations. The first value of a relation is an input value and the second value is the output value. A function is a specific type of relation in which each input value has one and only one output value. An input is the independent value, and the output value is the dependent value, as it depends on the value of the input. Notice in the first table below, where the input is “name” and the output is “age,” each input matches with exactly one output. This is an example of a function.
Family Member's Name (Input) Family Member's Age
Nellie 13
Marcos 11
Esther 46
Samuel 47
Nina 47
Paul 47
Katrina 21
Andrew 16
Maria 13
Ana 81
Compare this with the next table, where the input is “age” and the output is “name.” Some of the inputs result in more than one output. This is an example of a correspondence that is not a function.
Starting Information (Input) Family Member’s Age Related Information (Output) Family Member’s Name
11 Marcos
13 Nellie Maria
16 Andrew
21 Katrina
46 Esther
47 Samuel Nina Paul
81 Ana
Let’s look back at our examples to determine whether the relations are functions or not and under what circumstances. Remember that a relation is a function if there is only one output for each input.

Example

Fill in the table.
Input Output Function? Why or why not?
Name of senator Name of state
Name of state Name of senator
Time elapsed Height of a tossed ball
Height of a tossed ball Time elapsed
Number of cars Number of tires
Number of tires Number of cars

Answer:

Input Output Function? Why or why not?
Name of senator Name of state Yes For each input, there will only be one output because a senator only represents one state.
Name of state Name of senator No For each state that is an input, 2 names of senators would result because each state has two senators.
Time elapsed Height of a tossed ball Yes At a specific time, the ball has one specific height.
Height of a tossed ball Time elapsed No Remember that the ball was tossed up and fell down. So for a given height, there could be two different times when the ball was at that height. The input height can result in more than one output.
Number of cars Number of tires Yes For any input of a specific number of cars, there is one specific output representing the number of tires.
Number of tires Number of cars Yes For any input of a specific number of tires, there is one specific output representing the number of cars.

Relations can be written as ordered pairs of numbers or as numbers in a table of values. By examining the inputs (x-coordinates) and outputs (y-coordinates), you can determine whether or not the relation is a function. Remember, in a function each input has only one output. There is a name for the set of input values and another name for the set of output values for a function. The set of input values is called the domain of the function. And the set of output values is called the range of the function. If you have a set of ordered pairs, you can find the domain by listing all of the input values, which are the x-coordinates. And to find the range, list all of the output values, which are the y-coordinates. So for the following set of ordered pairs, [latex-display]\{(−2,0),(0,6),(2,12),(4,18)\}[/latex-display] You have the following: [latex-display]\begin{array}{l}\text{Domain}:\{−2,0,2,4\}\\\text{Range}:\{0,6,12,18\}\end{array}\\[/latex-display] You try it.

Example

List the domain and range for the following table of values where x is the input and y is the output.
x y
[latex]−3[/latex] [latex]4[/latex]
[latex]−2[/latex] [latex]4[/latex]
[latex]−1[/latex] [latex]4[/latex]
[latex]2[/latex] [latex]4[/latex]
[latex]3[/latex] [latex]4[/latex]

Answer: The domain describes all the inputs, and we can use set notation with brackets{} to make the list. [latex-display]\text{Domain}:\{-3,-2,-1,2,3\}\\[/latex-display] The range describes all the outputs. [latex-display]\text{Range}:\{4\}\\[/latex-display] We only listed 4 once because it is not necessary to list it every time it appears in the range.

In the following video we provide another example of identifying whether a table of values represents a function, as well as determining the domain and range of the sets. https://youtu.be/y2TqnP_6M1s

Example

Define the domain and range for the following set of ordered pairs, and determine whether the relation given is a function.

[latex]\{(−3,−6),(−2,−1),(1,0),(1,5),(2,0)\}[/latex]

Answer: We list all of the input values as the domain.  The input values are represented first in the ordered pair as a matter of convention. Domain: {-3,-2,1,2} Note how we didn't enter repeated values more than once, it is not necessary. The range is the list of outputs for the relation, they are entered second in the ordered pair. Range: {-6, -1, 0, 5} Organizing the ordered pairs in a table can help you tell whether this relation is a function.  By definition, the inputs in a function have only one output.

x y
[latex]−3[/latex] [latex]−6[/latex]
[latex]−2[/latex] [latex]−1[/latex]
[latex]1[/latex] [latex]0[/latex]
[latex]1[/latex] [latex]5[/latex]
[latex]2[/latex] [latex]0[/latex]

Answer

Domain: {-3,-2,1,2} Range: {-6, -1, 0, 5} The relation is not a function because the input 1 has two outputs: 0 and 5.

In the following video we show how to determine whether a relation is a function, and define the domain and range. https://youtu.be/kzgLfwgxE8g

Example

Define the domain and range of this relation and determine whether it is a function.

[latex]\{(−3, 4),(−2, 4),( −1, 4),(2, 4),(3, 4)\}[/latex]

Answer: Domain: {-3, -2, -1, 2, 3} Range: {4} To help you determine whether this is a function, you could reorganize the information by creating a table.

x y
[latex]−3[/latex] [latex]4[/latex]
[latex]−2[/latex] [latex]4[/latex]
[latex]−1[/latex] [latex]4[/latex]
[latex]2[/latex] [latex]4[/latex]
[latex]3[/latex] [latex]4[/latex]
Each input has only one output, and the fact that it is the same output (4) does not matter.

Answer

Domain: {-3, -2, -1, 2, 3} Range: {4} This relation is a function.

Some people think of functions as “mathematical machines.” Imagine you have a machine that changes a number according to a specific rule, such as “multiply by 3 and add 2” or “divide by 5, add 25, and multiply by [latex]−1[/latex].” If you put a number into the machine, a new number will pop out the other end, having been changed according to the rule. The number that goes in is called the input, and the number that is produced is called the output. You can also call the machine “[latex]f[/latex]” for function. If you put [latex]x[/latex] into the box, [latex]f(x)[/latex], comes out. Mathematically speaking, [latex]x[/latex] is the input, or the “independent variable,” and [latex]f(x)[/latex] is the output, or the “dependent variable,” since it depends on the value of [latex]x[/latex]. [latex]f(x)=4x+1[/latex] is written in function notation and is read “[latex]f[/latex] of [latex]x[/latex] equals [latex]4x[/latex] plus 1.” It represents the following situation: A function named [latex]f[/latex] acts upon an input, [latex]x[/latex], and produces [latex]f(x)[/latex] which is equal to [latex]4x+1[/latex]. This is the same as the equation as [latex]y=4x+1[/latex]. Function notation gives you more flexibility because you don’t have to use [latex]y[/latex] for every equation. Instead, you could use [latex]f(x)[/latex]  or [latex]g(x)[/latex] or [latex]c(x)[/latex]. This can be a helpful way to distinguish equations of functions when you are dealing with more than one at a time.

Using Function Notation

Once we determine that a relationship is a function, we need to display and define the functional relationships so that we can understand and use them, and sometimes also so that we can program them into computers. There are various ways of representing functions. A standard function notation is one representation that facilitates working with functions. Now you try it.

Example

Represent height as a function of age using function notation.

Answer: To represent "height is a function of age," we start by identifying the descriptive variables [latex]h[/latex] for height and [latex]a[/latex] for age. [latex-display]\begin{array}{ccc}h\text{ is }f\text{ of }a\hfill & \hfill & \hfill & \hfill & \text{We name the function }f;\text{ height is a function of age}.\hfill \\ h=f\left(a\right)\hfill & \hfill & \hfill & \hfill & \text{We use parentheses to indicate the function input}\text{. }\hfill \\ f\left(a\right)\hfill & \hfill & \hfill & \hfill & \text{We name the function }f;\text{ the expression is read as ''}f\text{ of }a\text{.''}\hfill \end{array}[/latex-display]

Analysis of the solution

We can use any letter to name the function; the notation [latex]h\left(a\right)[/latex] shows us that [latex]h[/latex] depends on [latex]a[/latex]. The value [latex]a[/latex] must be put into the function [latex]h[/latex] to get a result. The parentheses indicate that age is input into the function; they do not indicate multiplication. Let's try another.

Example

  1. Write the formula for perimeter of a square, [latex]P=4s[/latex], as a function.
  2. Write the formula for area of a square, [latex]A=l^{2}[/latex], as a function.

Answer:

  1. Name the function P. P is a function of the length of the sides, s. Perimeter as a function of side length is equal to 4 times side length. [latex]P(s)=4s[/latex]
  2. Name the function A.  Area as a function of the length of the sides is equal to the length squared.[latex]A(l)=l^{2}[/latex].

This would make it easy to graph both functions on the same graph without confusion about the variables. We can also give an algebraic expression as the input to a function. For example [latex]f\left(a+b\right)[/latex] means "first add [latex]a[/latex] and [latex]b[/latex], and the result is the input for the function [latex]f[/latex]." The operations must be performed in this order to obtain the correct result.

A General Note: Function Notation

The notation [latex]y=f\left(x\right)[/latex] defines a function named [latex]f[/latex]. This is read as "[latex]y[/latex] is a function of [latex]x[/latex]." The letter [latex]x[/latex] represents the input value, or independent variable. The letter y  or [latex]f\left(x\right)[/latex], represents the output value, or dependent variable.

Example

Use function notation to represent a function whose input is the name of a month and output is the number of days in that month.

Answer: The number of days in a month is a function of the name of the month, so if we name the function [latex]f[/latex], we write [latex]\text{days}=f\left(\text{month}\right)[/latex] or [latex]d=f\left(m\right)[/latex]. The name of the month is the input to a "rule" that associates a specific number (the output) with each input. The function 31 = f(January) where 31 is the output, f is the rule, and January is the input. For example, [latex]f\left(\text{March}\right)=31[/latex], because March has 31 days. The notation [latex]d=f\left(m\right)[/latex] reminds us that the number of days, [latex]d[/latex] (the output), is dependent on the name of the month, [latex]m[/latex] (the input).

Note that the inputs to a function do not have to be numbers; function inputs can be names of people, labels of geometric objects, or any other element that determines some kind of output. However, most of the functions we will work with in this book will have numbers as inputs and outputs.

Example

A function [latex]N=f\left(y\right)[/latex] gives the number of police officers, [latex]N[/latex], in a town in year [latex]y[/latex]. What does [latex]f\left(2005\right)=300[/latex] represent?

Answer: When we read [latex]f\left(2005\right)=300[/latex], we see that the input year is 2005. The value for the output, the number of police officers [latex]\left(N\right)[/latex], is 300. Remember, [latex]N=f\left(y\right)[/latex]. The statement [latex]f\left(2005\right)=300[/latex] tells us that in the year 2005 there were 300 police officers in the town.

In the following videos we show two more examples of how to express a relationship using function notation. https://youtu.be/lF0fzdaxU_8 https://youtu.be/nAF_GZFwU1g

Graphs of functions

When both the independent quantity (input) and the dependent quantity (output) are real numbers, a function can be represented by a graph in the coordinate plane. The independent value is plotted on the x-axis and the dependent value is plotted on the y-axis. The fact that each input value has exactly one output value means graphs of functions have certain characteristics. For each input on the graph, there will be exactly one output. For a function defined as [latex]y = f(x)[/latex], or [latex]y[/latex] is a function of [latex]x[/latex], we would write ordered pairs [latex](x, f(x))[/latex] using function notation instead of [latex](x,y)[/latex] as you may have seen previously. Coordinate axes with y-axis labeled f(x) and the x axis labeled x. We can identify whether the graph of a relation represents a function because for each x-coordinate there will be exactly one y-coordinate.

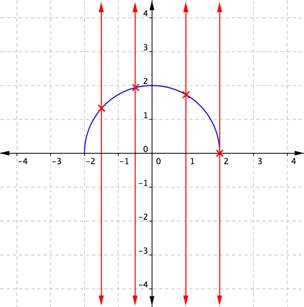
A graph of a semicircle. Four vertical lines cross the semicircle at one point each.

When a vertical line is placed across the plot of this relation, it does not intersect the graph more than once for any values of [latex]x[/latex]. If, on the other hand, a graph shows two or more intersections with a vertical line, then an input (x-coordinate) can have more than one output (y-coordinate), and [latex]y[/latex] is not a function of [latex]x[/latex]. Examining the graph of a relation to determine if a vertical line would intersect with more than one point is a quick way to determine if the relation shown by the graph is a function. This method is often called the “vertical line test.” You try it.

Example

Use the vertical line test to determine whether the relation plotted on this graph is a function. Graph with circle plotted - center at (0,0) radius = 2, more points include (2,0), (-2,0)

Answer: This relationship cannot be a function, because some of the x-coordinates have two corresponding y-coordinates.

A circle with four vertical lines through it. Three of the lines cross the circle at two points, and one line crosses the edge of the circle at one point.

The vertical line method can also be applied to a set of ordered pairs plotted on a coordinate plane to determine if the relation is a function.

Example

Consider the ordered pairs [latex]\{(−1,3),(−2,5),(−3,3),(−5,−3)\}[/latex], plotted on the graph below. Use the vertical line test to determine whether the set of ordered pairs represents a function.

The points (−1,3); (−2,5); (−3,3); and (−5,−3).

Answer:

Drawing vertical lines through each point results in each line only touching one point. This means that none of the x-coordinates have two corresponding y-coordinates, so this is a function.

Edit_Page_‹_Intermediate_Algebra_—_Pressbooks

In another set of ordered pairs, [latex]\{(3,−1),(5,−2),(3,−3),(−3,5)\}[/latex], one of the inputs, 3, can produce two different outputs, [latex]−1[/latex] and [latex]−3[/latex]. You know what that means—this set of ordered pairs is not a function. A plot confirms this.

The point negative 3, 5; the point 5, negative 2. A line through the points negative 1, 3; and the point negative 3, negative 3.

Notice that a vertical line passes through two plotted points. One x-coordinate has multiple y-coordinates. This relation is not a function. In the following video we show another example of determining whether a graph represents a function using the vertical line test. https://youtu.be/5Z8DaZPJLKY

Evaluate Functions

Throughout this course, you have been working with algebraic equations. Many of these equations are functions. For example, [latex]y=4x+1[/latex] is an equation that can also represent a function. When you input values for [latex]x[/latex], you can determine a single output for [latex]y[/latex]. In this case, if you substitute [latex]x=10[/latex] into the equation you will find that y must be 41; there is no other value of y that would make the equation true. Rather than using the variable [latex]y[/latex], the equations of functions can be written using function notation. Function notation is very useful when you are working with more than one function at a time, and substituting more than one variable in for [latex]x[/latex]. Equations written using function notation can also be evaluated. With function notation, you might see a problem like this. Given [latex]f(x)=4x+1[/latex], find [latex]f(2)[/latex] You read this problem like this: “given [latex]f[/latex] of [latex]x[/latex] equals [latex]4x[/latex] plus one, find [latex]f[/latex] of 2.” While the notation and wording is different, the process of evaluating a function is the same as evaluating an equation: in both cases, you substitute 2 for x, multiply it by 4 and add 1, simplifying to get 9. In both a function and an equation, an input of 2 results in an output of 9.

[latex]f(x)=4x+1\\f(2)=4(2)+1=8+1=9[/latex]

You can simply apply what you already know about evaluating expressions to evaluate a function. It’s important to note that the parentheses that are part of function notation do not mean multiply. The notation [latex]<i>f</i>(<i>x</i>)[/latex] does not mean [latex]f[/latex] multiplied by [latex]x[/latex]. Instead the notation means “[latex]f[/latex] of [latex]x[/latex]” or “the function of [latex]x[/latex]” To evaluate the function, take the value given for [latex]x[/latex], and substitute that value in for [latex]x[/latex] in the expression. Let’s look at a couple of examples.

Example

Given [latex]f(x)=3x–4[/latex], find [latex]f(5)[/latex].

Answer: Substitute 5 in for x in the function.

[latex]f(5)=3(5)-4[/latex]

Simplify the expression on the right side of the equation.

[latex]f(5)=15-4\\f(5)=11[/latex]

Answer

Given [latex]f(x)=3x–4[/latex], [latex]f(5)=11[/latex].

Functions can be evaluated for negative values of [latex]x[/latex], too. Keep in mind the rules for integer operations.

Example

Given [latex]p(x)=2x^{2}+5[/latex], find [latex]p(−3)[/latex].

Answer: Substitute [latex]-3[/latex] in for x in the function.

[latex]p(−3)=2(−3)^{2}+5[/latex]

Simplify the expression on the right side of the equation.

[latex]p(−3)=2(9)+5\\p(−3)=18+5\\p(−3)=23[/latex]

Answer

Given [latex]p(x)=2x^{2}+5[/latex], [latex]p(−3)=23[/latex].

You may also be asked to evaluate a function for more than one value as shown in the example that follows.

Example

Given [latex]f(x)=|4x-3|[/latex], find [latex]f(0)[/latex], [latex]f(2)[/latex], and [latex]f(−1)[/latex].

Answer: Treat each of these like three separate problems. In each case, you substitute the value in for x and simplify. Start with [latex]x=0[/latex].

[latex]f(0)=|4(0)-3|\\=|-3|\\f(0)=3[/latex]

Evaluate for [latex]x=2[/latex].

[latex]f(2)=|4(2)-3|\\=|5|\\f(2)=5[/latex]

Evaluate for [latex]x=−1[/latex].

[latex]f(−1)=|4(-1)-3|\\=|-7|\\f(-1)=7[/latex]

Answer

Given [latex]f(x)=|4x-3|[/latex], [latex]f(0)=3[/latex], [latex]f(2)=5[/latex], and [latex]f(‒1)=7[/latex].

Variable Inputs

So far, you have evaluated functions for inputs that have been constants. Functions can also be evaluated for inputs that are variables or expressions. The process is the same, but the simplified answer will contain a variable. The following examples show how to evaluate a function for a variable input.

Example

Given [latex]f(x)=3x^2+2x+1[/latex] find [latex]f(b)[/latex]

Answer: This problem is asking you to evaluate the function for [latex]b[/latex]. This means substitute [latex]b[/latex] in the equation for [latex]x[/latex]. [latex-display]f(b)=3b^{2}+2b+1[/latex-display] (That’s it—you’re done.)

Answer

Given [latex]f(x)=3x^{2}+2x+1[/latex], [latex]f(b)=3b^{2}+2b+1[/latex].

In the following example, you evaluate a function for an expression. So here you will substitute the entire expression in for [latex]x[/latex] and simplify.

Example

Given [latex]f(x)=4x+1[/latex], find [latex]f(h+1)[/latex].

Answer: This time, you substitute [latex](h+1)[/latex] into the equation for x. [latex]f(h+1)=4(h+1)+1[/latex]  Use the distributive property on the right side, and then combine like terms to simplify. [latex-display]f(h+1)=4h+4+1=4h+5[/latex-display]

Answer

Given [latex]f(x)=4x+1[/latex], [latex]f(h+1)=4h+5[/latex].

In the following video we show more examples of evaluating functions for both integer and variable inputs. https://youtu.be/_bi0B2zibOg  

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Ex 1: Find Domain and Range of Ordered Pairs, Function or Not. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • College Algebra. Provided by: OpenStax Located at: https://cnx.org/contents/[email protected]:1/Preface.. License: CC BY: Attribution.
  • Ex: Give the Domain and Range Given the Points in a Table. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex: Determine if a Table of Values Represents a Function. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex: Function Notation Application Problem. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Function Notation Application. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • College Algebra. Provided by: OpenStax Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution. License terms: Download for free at : http://cnx.org/contents/[email protected]:1/Preface.
  • Ex: Determine if a Table of Values Represents a Function. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex: Determine Various Function Outputs for a Quadratic Function. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.