Examples

Example 1: The population of elk in a national forest was measured to be 12,000 in 2003, and was measured again to be 15,000 in 2007. If the population continues to grow linearly at this rate, what will the elk population be in 2014?

Answer: The key phrase in this problem is "grow linearly."  This tells us that we will use a linear equation (or model).  To create our equation, we need to identify P­₀ and d.   First, we need to define how we’re going to measure n.   Remember that P­₀ is the population when n = 0, so we probably don’t want to literally use the year 0. Since we already know the population in 2003, let us define n to be the number of years since 2003.  Then, n = 0 corresponds to the year 2003 so that P­₀ = 12,000.   Next we need to find d. Remember d is the growth per time period, in this case growth per year. Between the two measurements, the population grew by 15,000-12,000 = 3,000, but it took 2007-2003 = 4 years to grow that much. To find the growth per year, we can divide: 3000 elk / 4 years = 750 elk in 1 year. Alternatively, you can use the slope formula from algebra to determine the common difference, noting that the population is the output of the formula, and time (number of years since 2003) is the input. [latex-display]d=\text{ slope }=\frac{\text{change in output}}{\text{change in input}}=\frac{15,000-12,000}{4-0}\frac{\text { elk}}{\text{ year }}=\frac{3000}{4} \frac{\text { elk}}{\text{ year }}=750 \text{ elk per year}[/latex-display] We can now write our equation:

P­_n = 12,000 + 750n

  To answer the question, we need to first note that the year 2014 will be n = 11, since 2014 is 11 years after 2003. Then we plug in 11 for n.

P­₁₁ = 12,000 + 750(11) = 20,250 elk

Thus, in 2014, this model predicts that there will be 20,250 elk in the national forest.  

This example is worked out in the following video.  Note that 43 seconds into the video, the presenter briefly mentions a "recursive" model--you may safely ignore this phrase since we have omitted this type of model from our course discussion. https://youtu.be/J1XqqlKzYGs

---

Example 2:  The cost, in dollars, of a gym membership for n months can be described by the explicit equation P­_n = 70 + 30n. What does this equation tell us?

Answer: The value for P­₀ in this equation is 70, so the initial starting cost is $70. This tells us that there must be an initiation or start-up fee of $70 to join the gym. The value for d in the equation is 30, so the cost increases by $30 each month. This tells us that the monthly membership fee for the gym is $30 a month.

The explanation for this example is detailed in the video below. https://youtu.be/0Uwz5dmLTtk

Example

Gasoline consumption in the US has been increasing steadily. Gasoline consumption data from 1992 to 2004 are shown below.[footnote]http://www.bts.gov/publications/national_transportation_statistics/2005/html/table_04_10.html[/footnote]

Year	'92	'93	'94	'95	'96	'97	'98	'99	'00	'01	'02	'03	'04
Consumption (billion of gallons)	110	111	113	116	118	119	123	125	126	128	131	133	136

1. Find a model for these data, and use it to predict consumption in 2016.
2. If the trend continues, when do you predict gasoline consumption to reach 200 billion gallons?

 

Answer: Since we are given data points, it is a great idea to begin by plotting these data: Notice that the data appear to have an approximately (not precisely) linear relationship.   While there are many advanced modeling and statistical techniques that can be used to find an equation to model the data, to get an idea of what is happening, we can find an equation by using two pieces of the data – perhaps the data from 1993 and 2003.  [Note: You could have chosen any two years but do note that your answers would likely be a little different from ours--and this is OKAY!  We are creating an imperfect model (an approximating model) for data that are only approximately linear.]   Let's define n be the number of years since 1993.  Then, n = 0 corresponds with 1993 giving P­₀ = 111 billion gallons and n = 10 corresponds with 2003. To find d, we need to know how much the gas consumption increased each year, on average. From 1993 to 2003 the gas consumption increased from 111 billion gallons to 133 billion gallons, a total change of 133 – 111 = 22 billion gallons over 10 years. This gives us an average change of 22 billion gallons / 10 year = 2.2 billion gallons per year. Equivalently, [latex]d=\text{ slope }=\frac{\text{change in output}}{\text{change in input}}=\frac{133-111}{10-0} \frac{\text{ billion gallons }}{\text{ year }}=\frac{22}{10} \frac{\text{ billion gallons }}{\text{ year }}=2.2[/latex] billion gallons per year. Thus, gas consumption is changing, on average, by approximately 2.2 billion gallons per year.  We now have enough information to write our equation: P­_n = 111 + 2.2n 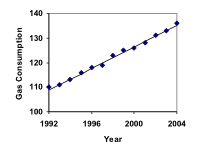  Calculating values using the explicit form and plotting them with the original data shows how well our model fits the data.  It looks like a pretty good approximation to the given data.  Now, we can use our model to make predictions about the future (or even the past!), assuming that this data trend is consistent before 1992 and after 2004. To predict the gasoline consumption in 2016, notice that n = 23 since 2016 – 1993 = 23 years.

P_­23 = 111 + 2.2(23) = 161.6

Our model predicts that the US will consume 161.6 billion gallons of gasoline in 2016, if the current trend continues.  This is the answer to our first question.   Next, we need to find when the gasoline consumption will reach 200 billion gallons.  We need to set the output, P­_n  equal to 200, and solve for n:

P_n = 200                                  Replace P_n with our model

200 = 111 + 2.2n                     Subtract 111 from both sides

 89  = 2.2n                               Divide both sides by 2.2

40.4545 = n

Our model predicts that gasoline consumption will reach 200 billion about 40 years after 1993, which would be in the year 2033.

  The steps for reaching this answer are detailed in the following video.   https://youtu.be/ApFxDWd6IbE

Example

Suppose a four year old boy is currently 39 inches tall, and you are told to expect him to grow 2.5 inches a year.  We can set up a growth model, with n defined to be the number of years past 4 (years old).  That is, n = 0 corresponds to when the child is 4 years old.  Thus, P₀ = 39 inches and d = 2.5 inches per year giving us the model:

P­_n = 39 + 2.5n

So at 6 years old, we would expect him to be: P­₂ = 39 + 2.5(2) = 44 inches tall   Of course, we wouldn’t expect this boy to continue to grow at the same rate all his life. If he did, at age 50 he would be P_­46 = 39 + 2.5(46) = 154 inches tall = 12.8 feet tall!   Important Idea: When using any mathematical model, we have to consider which inputs are reasonable to use. Whenever we make predictions into the future (the mathematical word for this is we extrapolate), we are making an assumption that the model will continue to be valid.  We must take care to ensure that this is indeed a reasonable assumption to make.   View a video explanation of this breakdown of the linear growth model here. https://youtu.be/6zfXCsmcDzI