Elements of Graph Theory
Learning Outcomes
- Identify the vertices, edges, and loops of a graph
- Identify the degree of a vertex
- Identify and draw both a path and a circuit through a graph
- Determine whether a graph is connected or disconnected
In the modern world, planning efficient routes is essential for business and industry, with applications as varied as product distribution, laying new fiber optic lines for broadband internet, and suggesting new friends within social network websites like Facebook.
This field of mathematics started nearly 300 years ago as a look into a mathematical puzzle (we’ll look at it in a bit). The field has exploded in importance in the last century, both because of the growing complexity of business in a global economy and because of the computational power that computers have provided us.
mathematical vocabulary
In mathematics, familiar words are often used in ways that are not familiar to you. That's because, as a new branch of mathematics is developed, a new vocabulary is built to describe it using the vernacular of the place and time in which it was developed. Graph theory is a relatively young branch of mathematics so it borrowed from words that are used commonly in our language.
A good way to make new mathematical usages familiar is by using flashcards. Write the word on one side and the definition on the other. Work your way through the pile once by looking at the definition, trying to give the proper word. Then, shuffle the cards and work through them again by looking at the word and trying to give the proper definition.
After working through the flashcards to memorize the new usages, build long-term memory by using the words in context. Read the text sections and try the examples and Try It problems, being careful to use the words in context. If possible, look for opportunities to use the vocabulary aloud in class.
This section contains a large number of new word usages. Don't gloss over these words and their mathematical definitions!
Drawing Graphs
Example
Here is a portion of a housing development from Missoula, Montana. As part of her job, the development’s lawn inspector has to walk down every street in the development making sure homeowners’ landscaping conforms to the community requirements.

Naturally, she wants to minimize the amount of walking she has to do. Is it possible for her to walk down every street in this development without having to do any backtracking? While you might be able to answer that question just by looking at the picture for a while, it would be ideal to be able to answer the question for any picture regardless of its complexity.
To do that, we first need to simplify the picture into a form that is easier to work with. We can do that by drawing a simple line for each street. Where streets intersect, we will place a dot.
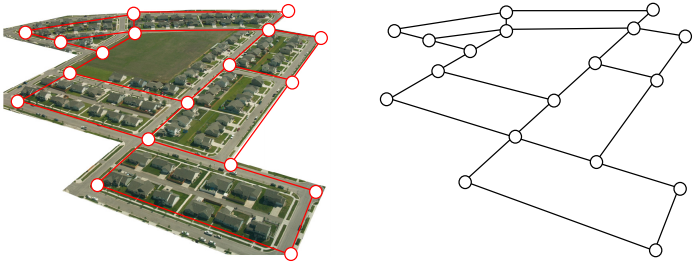
This type of simplified picture is called a graph.
Graphs, Vertices, and Edges
A graph consists of a set of dots, called vertices, and a set of edges connecting pairs of vertices.
While we drew our original graph to correspond with the picture we had, there is nothing particularly important about the layout when we analyze a graph. Both of the graphs below are equivalent to the one drawn above.
 You probably already noticed that we are using the term graph differently than you may have used the term in the past to describe the graph of a mathematical function.
Watch the video below to get another perspective of drawing a street network graph.
https://youtu.be/gyQhW24Dr2E
You probably already noticed that we are using the term graph differently than you may have used the term in the past to describe the graph of a mathematical function.
Watch the video below to get another perspective of drawing a street network graph.
https://youtu.be/gyQhW24Dr2E
Example

Back in the 18th century in the Prussian city of Königsberg, a river ran through the city and seven bridges crossed the forks of the river. The river and the bridges are highlighted in the picture to the right.[footnote]Bogdan Giuşcă. http://en.wikipedia.org/wiki/File:Konigsberg_bridges.png[/footnote]
As a weekend amusement, townsfolk would see if they could find a route that would take them across every bridge once and return them to where they started.
In the following video we present another view of the Königsberg bridge problem.
https://youtu.be/yn-OD8OBSDM
Leonard Euler (pronounced OY-lur), one of the most prolific mathematicians ever, looked at this problem in 1735, laying the foundation for graph theory as a field in mathematics. To analyze this problem, Euler introduced edges representing the bridges:
 Since the size of each land mass it is not relevant to the question of bridge crossings, each can be shrunk down to a vertex representing the location:
Since the size of each land mass it is not relevant to the question of bridge crossings, each can be shrunk down to a vertex representing the location:
 Notice that in this graph there are two edges connecting the north bank and island, corresponding to the two bridges in the original drawing. Depending upon the interpretation of edges and vertices appropriate to a scenario, it is entirely possible and reasonable to have more than one edge connecting two vertices.
While we haven’t answered the actual question yet of whether or not there is a route which crosses every bridge once and returns to the starting location, the graph provides the foundation for exploring this question.
Notice that in this graph there are two edges connecting the north bank and island, corresponding to the two bridges in the original drawing. Depending upon the interpretation of edges and vertices appropriate to a scenario, it is entirely possible and reasonable to have more than one edge connecting two vertices.
While we haven’t answered the actual question yet of whether or not there is a route which crosses every bridge once and returns to the starting location, the graph provides the foundation for exploring this question.
Definitions
While we loosely defined some terminology earlier, we now will try to be more specific.
Vertex
A vertex is a dot in the graph that could represent an intersection of streets, a land mass, or a general location, like “work” or “school”. Vertices are often connected by edges. Note that vertices only occur when a dot is explicitly placed, not whenever two edges cross. Imagine a freeway overpass—the freeway and side street cross, but it is not possible to change from the side street to the freeway at that point, so there is no intersection and no vertex would be placed.
Edges
Edges connect pairs of vertices. An edge can represent a physical connection between locations, like a street, or simply that a route connecting the two locations exists, like an airline flight.
Loop
A loop is a special type of edge that connects a vertex to itself. Loops are not used much in street network graphs.

Path
A path is a sequence of vertices using the edges. Usually we are interested in a path between two vertices. For example, a path from vertex A to vertex M is shown below. It is one of many possible paths in this graph.

Circuit
A circuit is a path that begins and ends at the same vertex. A circuit starting and ending at vertex A is shown below.

Connected
A graph is connected if there is a path from any vertex to any other vertex. Every graph drawn so far has been connected. The graph below is
disconnected; there is no way to get from the vertices on the left to the vertices on the right.

Weights
Depending upon the problem being solved, sometimes weights are assigned to the edges. The weights could represent the distance between two locations, the travel time, or the travel cost. It is important to note that the distance between vertices in a graph does not necessarily correspond to the weight of an edge.
Try It
1.The graph below shows 5 cities. The weights on the edges represent the airfare for a one -way flight between the cities.
a. How many vertices and edges does the graph have?
b. Is the graph connected?
c. What is the degree of the vertex representing LA?
d. If you fly from Seattle to Dallas to Atlanta, is that a path or a circuit?
e. If you fly from LA to Chicago to Dallas to LA, is that a path or a circuit.

[embed]https://www.myopenmath.com/multiembedq.php?id=6883&theme=oea&iframe_resize_id=mom5[/embed]
[embed]https://www.myopenmath.com/multiembedq.php?id=6885&theme=oea&iframe_resize_id=mom1[/embed]
Licenses & Attributions
CC licensed content, Original
CC licensed content, Shared previously
- Graph Theory. Authored by: David Lippman. Located at: http://www.opentextbookstore.com/mathinsociety/. License: CC BY: Attribution.
- Pleasant View housing development. Authored by: Sam Beebe. Located at: https://www.flickr.com/photos/sbeebe/2850476641/. License: CC BY: Attribution.
- Drawing a street network graph. License: Public Domain: No Known Copyright.
- Drawing a graph for bridges. Authored by: OCLPhase2. License: CC BY: Attribution.
- Question ID 6885, 6883. Authored by: Lippman, David. License: CC BY: Attribution. License terms: IMathAS Community License, CC-BY + GPL.
 Naturally, she wants to minimize the amount of walking she has to do. Is it possible for her to walk down every street in this development without having to do any backtracking? While you might be able to answer that question just by looking at the picture for a while, it would be ideal to be able to answer the question for any picture regardless of its complexity.
To do that, we first need to simplify the picture into a form that is easier to work with. We can do that by drawing a simple line for each street. Where streets intersect, we will place a dot.
Naturally, she wants to minimize the amount of walking she has to do. Is it possible for her to walk down every street in this development without having to do any backtracking? While you might be able to answer that question just by looking at the picture for a while, it would be ideal to be able to answer the question for any picture regardless of its complexity.
To do that, we first need to simplify the picture into a form that is easier to work with. We can do that by drawing a simple line for each street. Where streets intersect, we will place a dot.

 You probably already noticed that we are using the term graph differently than you may have used the term in the past to describe the graph of a mathematical function.
Watch the video below to get another perspective of drawing a street network graph.
https://youtu.be/gyQhW24Dr2E
You probably already noticed that we are using the term graph differently than you may have used the term in the past to describe the graph of a mathematical function.
Watch the video below to get another perspective of drawing a street network graph.
https://youtu.be/gyQhW24Dr2E
 Back in the 18th century in the Prussian city of Königsberg, a river ran through the city and seven bridges crossed the forks of the river. The river and the bridges are highlighted in the picture to the right.[footnote]Bogdan Giuşcă. http://en.wikipedia.org/wiki/File:Konigsberg_bridges.png[/footnote]
As a weekend amusement, townsfolk would see if they could find a route that would take them across every bridge once and return them to where they started.
Back in the 18th century in the Prussian city of Königsberg, a river ran through the city and seven bridges crossed the forks of the river. The river and the bridges are highlighted in the picture to the right.[footnote]Bogdan Giuşcă. http://en.wikipedia.org/wiki/File:Konigsberg_bridges.png[/footnote]
As a weekend amusement, townsfolk would see if they could find a route that would take them across every bridge once and return them to where they started.
 Since the size of each land mass it is not relevant to the question of bridge crossings, each can be shrunk down to a vertex representing the location:
Since the size of each land mass it is not relevant to the question of bridge crossings, each can be shrunk down to a vertex representing the location:
 Notice that in this graph there are two edges connecting the north bank and island, corresponding to the two bridges in the original drawing. Depending upon the interpretation of edges and vertices appropriate to a scenario, it is entirely possible and reasonable to have more than one edge connecting two vertices.
While we haven’t answered the actual question yet of whether or not there is a route which crosses every bridge once and returns to the starting location, the graph provides the foundation for exploring this question.
Notice that in this graph there are two edges connecting the north bank and island, corresponding to the two bridges in the original drawing. Depending upon the interpretation of edges and vertices appropriate to a scenario, it is entirely possible and reasonable to have more than one edge connecting two vertices.
While we haven’t answered the actual question yet of whether or not there is a route which crosses every bridge once and returns to the starting location, the graph provides the foundation for exploring this question.







 [embed]https://www.myopenmath.com/multiembedq.php?id=6883&theme=oea&iframe_resize_id=mom5[/embed]
[embed]https://www.myopenmath.com/multiembedq.php?id=6885&theme=oea&iframe_resize_id=mom1[/embed]
[embed]https://www.myopenmath.com/multiembedq.php?id=6883&theme=oea&iframe_resize_id=mom5[/embed]
[embed]https://www.myopenmath.com/multiembedq.php?id=6885&theme=oea&iframe_resize_id=mom1[/embed]
