We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Mathematics for the Liberal Arts Corequisite

Finding the Least Common Multiple of Two Numbers

Learning Outcomes

  • Find the least common multiple of two numbers by listing multiples
  • Find the least common multiple of two numbers by prime factorization
One of the reasons we find multiples and primes is to use them to find the least common multiple of two numbers. This will be useful when we add and subtract fractions with different denominators.

Listing Multiples Method

A common multiple of two numbers is a number that is a multiple of both numbers. Suppose we want to find common multiples of [latex]10[/latex] and [latex]25[/latex]. We can list the first several multiples of each number. Then we look for multiples that are common to both lists—these are the common multiples.

[latex]\begin{array}{c}10\text{ : }10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110\ldots \hfill \\ 25\text{ : }25, 50,75, 100, 125\ldots \hfill \end{array}[/latex]

We see that [latex]50[/latex] and [latex]100[/latex] appear in both lists. They are common multiples of [latex]10[/latex] and [latex]25[/latex]. We would find more common multiples if we continued the list of multiples for each. The smallest number that is a multiple of two numbers is called the least common multiple (LCM). So the least LCM of [latex]10[/latex] and [latex]25[/latex] is [latex]50[/latex].

Find the least common multiple (LCM) of two numbers by listing multiples

  1. List the first several multiples of each number.
  2. Look for multiples common to both lists. If there are no common multiples in the lists, write out additional multiples for each number.
  3. Look for the smallest number that is common to both lists.
  4. This number is the LCM.
 

example

Find the LCM of [latex]15[/latex] and [latex]20[/latex] by listing multiples. Solution: List the first several multiples of [latex]15[/latex] and of [latex]20[/latex]. Identify the first common multiple.

[latex]\begin{array}{l}\text{15: }15,30,45,60,75,90,105,120\hfill \\ \text{20: }20,40,60,80,100,120,140,160\hfill \end{array}[/latex]

The smallest number to appear on both lists is [latex]60[/latex], so [latex]60[/latex] is the least common multiple of [latex]15[/latex] and [latex]20[/latex]. Notice that [latex]120[/latex] is on both lists, too. It is a common multiple, but it is not the least common multiple.
 

try it

[ohm_question]145458[/ohm_question]
In the next video we show an example of how to find the Least Common Multiple by listing multiples of each number. https://youtu.be/7twRSmgcrLM

Prime Factors Method

Another way to find the least common multiple of two numbers is to use their prime factors. We’ll use this method to find the LCM of [latex]12[/latex] and [latex]18[/latex]. We start by finding the prime factorization of each number.

[latex]12=2\cdot 2\cdot 318=2\cdot 3\cdot 3[/latex]

Then we write each number as a product of primes, matching primes vertically when possible.

[latex]\begin{array}{l}12=2\cdot 2\cdot 3\hfill \\ 18=2\cdot 3\cdot 3\end{array}[/latex]

Now we bring down the primes in each column. The LCM is the product of these factors.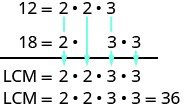 The image shows the prime factorization of 12 written as the equation 12 equals 2 times 2 times 3. Below this equation is another showing the prime factorization of 18 written as the equation 18 equals 2 times 3 times 3. The two equations line up vertically at the equal symbol. The first 2 in the prime factorization of 12 aligns with the 2 in the prime factorization of 18. Under the second 2 in the prime factorization of 12 is a gap in the prime factorization of 18. Under the 3 in the prime factorization of 12 is the first 3 in the prime factorization of 18. The second 3 in the prime factorization has no factors above it from the prime factorization of 12. A horizontal line is drawn under the prime factorization of 18. Below this line is the equation LCM equal to 2 times 2 times 3 times 3. Arrows are drawn down vertically from the prime factorization of 12 through the prime factorization of 18 ending at the LCM equation. The first arrow starts at the first 2 in the prime factorization of 12 and continues down through the 2 in the prime factorization of 18. Ending with the first 2 in the LCM. The second arrow starts at the next 2 in the prime factorization of 12 and continues down through the gap in the prime factorization of 18. Ending with the second 2 in the LCM. The third arrow starts at the 3 in the prime factorization of 12 and continues down through the first 3 in the prime factorization of 18. Ending with the first 3 in the LCM. The last arrow starts at the second 3 in the prime factorization of 18 and points down to the second 3 in the LCM. Notice that the prime factors of [latex]12[/latex] and the prime factors of [latex]18[/latex] are included in the LCM. By matching up the common primes, each common prime factor is used only once. This ensures that [latex]36[/latex] is the least common multiple.

Find the LCM using the prime factors method

  1. Find the prime factorization of each number.
  2. Write each number as a product of primes, matching primes vertically when possible.
  3. Bring down the primes in each column.
  4. Multiply the factors to get the LCM.
 

example

Find the LCM of [latex]15[/latex] and [latex]18[/latex] using the prime factors method.

Answer: Solution:

Write each number as a product of primes. .
Write each number as a product of primes, matching primes vertically when possible. .
Bring down the primes in each column. .
Multiply the factors to get the LCM. [latex]\text{LCM}=2\cdot 3\cdot 3\cdot 5[/latex]The LCM of [latex]15\text{ and }18\text{ is } 90[/latex].

 

try it

[embed]
 

example

Find the LCM of [latex]50[/latex] and [latex]100[/latex] using the prime factors method.

Answer: Solution:

Write the prime factorization of each number. [latex]50=2\cdot{5}\cdot{5}\quad\quad\quad{100=2\cdot{2}\cdot{5}\cdot{5}}[/latex]
Write each number as a product of primes, matching primes vertically when possible. [latex]50=\quad{2\cdot{5}\cdot{5}}[/latex][latex]100=2\cdot{2}\cdot{5}\cdot{5}[/latex]
Bring down the primes in each column. .
Multiply the factors to get the LCM. [latex]\text{LCM}=2\cdot 2\cdot 5\cdot 5[/latex]The LCM of [latex]50\text{ and } 100\text{ is } 100[/latex].

 

try it

[ohm_question]145462[/ohm_question]
In the next video we show how to find the Least Common Multiple by using prime factorization. https://youtu.be/hZvRDG-HgMY

Licenses & Attributions

CC licensed content, Original

  • Question ID: 145462, 145459, 145458. Authored by: Alyson Day. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.

CC licensed content, Shared previously

  • Example: Determining the Least Common Multiple Using a List of Multiples. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Example: Determining the Least Common Multiple Using Prime Factorization. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.

CC licensed content, Specific attribution