We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

学習ガイド > College Algebra CoRequisite Course

Synthetic Division

Learning Outcomes

  • Use synthetic division to divide polynomials.
As we’ve seen, long division with polynomials can involve many steps and be quite cumbersome. Synthetic division is a shorthand method of dividing polynomials for the special case of dividing by a linear factor whose leading coefficient is 1. To illustrate the process, recall the example at the beginning of the section. Divide [latex]2{x}^{3}-3{x}^{2}+4x+5[/latex] by [latex]x+2[/latex] using the long division algorithm. The final form of the process looked like this: cnx_precalc_revised_eq_42 There is a lot of repetition in the table. If we don’t write the variables but instead line up their coefficients in columns under the division sign and also eliminate the partial products, we already have a simpler version of the entire problem. Synthetic division of the polynomial 2x^3-3x^2+4x+5 by x+2 in which it only contains the coefficients of each polynomial.   Synthetic division carries this simplification even a few more steps. Collapse the table by moving each of the rows up to fill any vacant spots. Also, instead of dividing by 2, as we would in division of whole numbers, and then multiplying and subtracting the middle product, we change the sign of the "divisor" to –2, multiply, and add. The process starts by bringing down the leading coefficient. Synthetic division of the polynomial 2x^3-3x^2+4x+5 by x+2 in which it only contains the coefficients of each polynomial. We then multiply it by the "divisor" and add, repeating this process column by column until there are no entries left. The bottom row represents the coefficients of the quotient; the last entry of the bottom row is the remainder. In this case, the quotient is [latex]2x{^2} -7x+18[/latex] and the remainder is –31. The process will be made more clear in the examples that follow.

A General Note: Synthetic Division

Synthetic division is a shortcut that can be used when the divisor is a binomial in the form x – k. In synthetic division, only the coefficients are used in the division process.

How To: Given two polynomials, use synthetic division to divide

  1. Write k for the divisor.
  2. Write the coefficients of the dividend.
  3. Bring the leading coefficient down.
  4. Multiply the leading coefficient by k. Write the product in the next column.
  5. Add the terms of the second column.
  6. Multiply the result by k. Write the product in the next column.
  7. Repeat steps 5 and 6 for the remaining columns.
  8. Use the bottom numbers to write the quotient. The number in the last column is the remainder and has degree 0, the next number from the right has degree 1, the next number from the right has degree 2, and so on.

Example: Using Synthetic Division to Divide a Second-Degree Polynomial

Use synthetic division to divide [latex]5{x}^{2}-3x - 36[/latex] by [latex]x - 3[/latex].

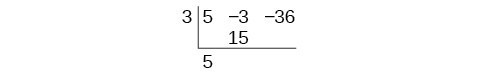Answer: Begin by setting up the synthetic division. Write k and the coefficients. A collapsed version of the previous synthetic division.   Bring down the leading coefficient. Multiply the leading coefficient by k. The set-up of the synthetic division for the polynomial 5x^2-3x-36 by x-3, which renders {5, -3, -36} by 3.   Continue by adding the numbers in the second column. Multiply the resulting number by k. Write the result in the next column. Then add the numbers in the third column. Multiplied by the lead coefficient, 5, in the second column, and the lead coefficient is brought down to the second row.   The result is [latex]5x+12[/latex]. The remainder is 0. So [latex]x - 3[/latex] is a factor of the original polynomial.

Analysis of the Solution

Just as with long division, we can check our work by multiplying the quotient by the divisor and adding the remainder. [latex-display]\left(x - 3\right)\left(5x+12\right)+0=5{x}^{2}-3x - 36[/latex-display]

Example: Using Synthetic Division to Divide a Third-Degree Polynomial

Use synthetic division to divide [latex]4{x}^{3}+10{x}^{2}-6x - 20[/latex] by [latex]x+2[/latex].

Answer: The binomial divisor is [latex]x+2[/latex], so [latex]k=-2[/latex]. Add each column, multiply the result by –2, and repeat until the last column is reached. Synthetic division of 4x^3+10x^2-6x-20 divided by x+2. The result is [latex]4{x}^{2}+2x - 10[/latex]. The remainder is 0. Thus, [latex]x+2[/latex] is a factor of [latex]4{x}^{3}+10{x}^{2}-6x - 20[/latex].

Analysis of the Solution

The graph of the polynomial function [latex]f\left(x\right)=4{x}^{3}+10{x}^{2}-6x - 20[/latex] shows a zero at [latex]x=-2[/latex]. This confirms that [latex]x+2[/latex] is a factor of [latex]4{x}^{3}+10{x}^{2}-6x - 20[/latex]. Synthetic division of 4x^3+10x^2-6x-20 divided by x+2.

Example: Using Synthetic Division to Divide a Fourth-Degree Polynomial

Use synthetic division to divide [latex]-9{x}^{4}+10{x}^{3}+7{x}^{2}-6[/latex] by [latex]x - 1[/latex].

Answer: Notice there is no x term. We will use a zero as the coefficient for that term. . The result is [latex]-9{x}^{3}+{x}^{2}+8x+8+\frac{2}{x - 1}[/latex].

Try It

Use synthetic division to divide [latex]3{x}^{4}+18{x}^{3}-3x+40[/latex] by [latex]x+7[/latex].

Answer: [latex]3{x}^{3}-3{x}^{2}+21x - 150+\frac{1,090}{x+7}[/latex]

Polynomial division can be used to solve a variety of application problems involving expressions for area and volume. We looked at an application at the beginning of this section. Now we will solve that problem in the following example.

Example: Using Polynomial Division in an Application Problem

The volume of a rectangular solid is given by the polynomial [latex]3{x}^{4}-3{x}^{3}-33{x}^{2}+54x[/latex]. The length of the solid is given by 3x and the width is given by x – 2. Find the height of the solid.

Answer: There are a few ways to approach this problem. We need to divide the expression for the volume of the solid by the expressions for the length and width. Let us create a sketch. Graph of f(x)=4x^3+10x^2-6x-20 with a close up on x+2. We can now write an equation by substituting the known values into the formula for the volume of a rectangular solid.

[latex]\begin{array}{l}V=l\cdot w\cdot h\\ 3{x}^{4}-3{x}^{3}-33{x}^{2}+54x=3x\cdot \left(x - 2\right)\cdot h\end{array}[/latex]

To solve for h, first divide both sides by 3x.

[latex]\begin{array}{l}\frac{3x\cdot \left(x - 2\right)\cdot h}{3x}=\frac{3{x}^{4}-3{x}^{3}-33{x}^{2}+54x}{3x}\\ \left(x - 2\right)h={x}^{3}-{x}^{2}-11x+18\end{array}[/latex]

Now solve for h using synthetic division.

[latex]h=\frac{{x}^{3}-{x}^{2}-11x+18}{x - 2}[/latex]

Synthetic division with 2 as the divisor and {1, -1, -11, 18} as the quotient. The result is {1, 1, -9, 0} The quotient is [latex]{x}^{2}+x - 9[/latex] and the remainder is 0. The height of the solid is [latex]{x}^{2}+x - 9[/latex].

Try It

The area of a rectangle is given by [latex]3{x}^{3}+14{x}^{2}-23x+6[/latex]. The width of the rectangle is given by x + 6. Find an expression for the length of the rectangle.

Answer: [latex]3{x}^{2}-4x+1[/latex]

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Question ID 29483. Authored by: McClure,Caren. License: Other. License terms: IMathAS Community License CC-BY + GPL.
  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].