Solve Systems of Three Equations in Three Variables
Learning Outcomes
- Determine whether an ordered triple is a solution to a system of three equations.
- Use back substitution to find a solution to a system of three equations.
- Write the equations for a system given a scenario, and solve.
- Interchange the order of any two equations.
- Multiply both sides of an equation by a nonzero constant.
- Add a nonzero multiple of one equation to another equation.
A General Note: Number of Possible Solutions
The planes illustrate possible solution scenarios for three-by-three systems.- Systems that have a single solution are those which, after elimination, result in a solution set consisting of an ordered triple [latex]\left\{\left(x,y,z\right)\right\}[/latex]. Graphically, the ordered triple defines a point that is the intersection of three planes in space.
- Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as [latex]0=0[/latex]. Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space.
- Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as [latex]3=0[/latex]. Graphically, a system with no solution is represented by three planes with no point in common.
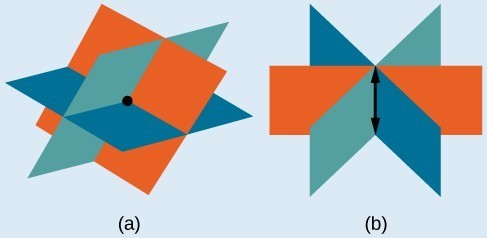 (a)Three planes intersect at a single point, representing a three-by-three system with a single solution. (b) Three planes intersect in a line, representing a three-by-three system with infinite solutions.
(a)Three planes intersect at a single point, representing a three-by-three system with a single solution. (b) Three planes intersect in a line, representing a three-by-three system with infinite solutions.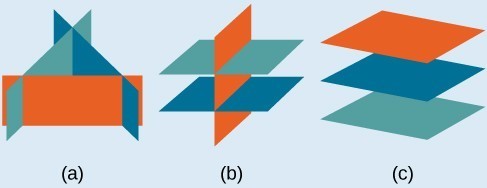
Example: Determining Whether an Ordered Triple Is a Solution to a System
Determine whether the ordered triple [latex]\left(3,-2,1\right)[/latex] is a solution to the system.[latex]\begin{array}{l}\text{ }x+y+z=2\hfill \\ 6x - 4y+5z=31\hfill \\ 5x+2y+2z=13\hfill \end{array}[/latex]
Answer: We will check each equation by substituting in the values of the ordered triple for [latex]x,y[/latex], and [latex]z[/latex].
[latex]\begin{align} x+y+z=2\\ \left(3\right)+\left(-2\right)+\left(1\right)=2\\ \text{True}\end{align}\hspace{5mm}[/latex] [latex]\hspace{5mm}\begin{align} 6x - 4y+5z=31\\ 6\left(3\right)-4\left(-2\right)+5\left(1\right)=31\\ 18+8+5=31\\ \text{True}\end{align}\hspace{5mm}[/latex] [latex]\hspace{5mm}\begin{align}5x+2y+2z=13\\ 5\left(3\right)+2\left(-2\right)+2\left(1\right)=13\\ 15 - 4+2=13\\ \text{True}\end{align}[/latex]
The ordered triple [latex]\left(3,-2,1\right)[/latex] is indeed a solution to the system.How To: Given a linear system of three equations, solve for three unknowns.
- Pick any pair of equations and solve for one variable.
- Pick another pair of equations and solve for the same variable.
- You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
- Back-substitute known variables into any one of the original equations and solve for the missing variable.
tip for success
Work through the following examples on paper in the order given. They slowly build up the technique of solving a three-by-three system in stages. Then you will have an opportunity to practice the 4-step process given in the How To box above.Example
Solve the given system. [latex-display]\displaystyle\begin{cases}x-\dfrac{1}{3}y+\dfrac{1}{2}z=1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,y-\dfrac{1}{2}z=4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,z=-1\end{cases}[/latex-display]Answer: The third equation states that [latex]z = −1[/latex], so we substitute this into the second equation to obtain a solution for [latex]y[/latex]. [latex-display]\begin{array}{l}y-\dfrac{1}{2}(-1)=4\\y+\dfrac{1}{2}=4\\y=4-\dfrac{1}{2}\\y=\dfrac{8}{2}-\dfrac{1}{2}\\y=\dfrac{7}{2}\end{array}[/latex-display] Now we have two of our solutions, and we can substitute them both into the first equation to solve for [latex]x[/latex]. [latex-display]\begin{array}{l}x-\dfrac{1}{3}\left(\dfrac{7}{2}\right)+\dfrac{1}{2}\left(-1\right)=1\\x-\dfrac{7}{6}-\dfrac{1}{2}=1\\x-\dfrac{7}{6}-\dfrac{3}{6}=1\\x-\dfrac{10}{6}=1\\x=1+\dfrac{10}{6}\\x=\dfrac{6}{6}+\dfrac{10}{6}\\x=\dfrac{16}{6}=\dfrac{8}{3}\end{array}[/latex-display] Now we have our ordered triple; remember to place each variable solution in order. [latex-display](x,y,z)=\left(\dfrac{8}{3},\dfrac{7}{2},-1\right)[/latex-display] Analysis of the Solution: Each of the lines in the system above represents a plane (think about a sheet of paper). If you imagine three sheets of notebook paper each representing a portion of these planes, you will start to see the complexities involved in how three such planes can intersect. Below is a sketch of the three planes. It turns out that any two of these planes intersect in a line, so our intersection point is where all three of these lines meet.
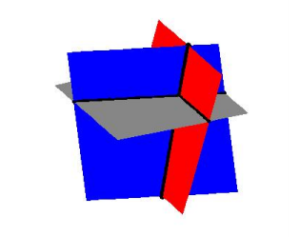 Three planes intersecting.
Three planes intersecting.Example
Find a solution to the following system:Answer: We labeled the equations this time to be able to keep track of things a little more easily. The most obvious first step here is to eliminate [latex]y[/latex] by adding equations (2) and (3).
[latex]\begin{array}{rrr}-2y+(6)=6\\-2y=6-6\\-2y=0\\\,\,\,\,y=0\end{array}[/latex]
Be careful here not to get confused with a solution of [latex]y = 0[/latex] and an inconsistent solution. It is ok for variables to equal [latex]0[/latex]. Now we can substitute [latex]z = 6[/latex] and [latex]y = 0[/latex] back into the first equation.[latex]\begin{array}{rrr}x-y+z=5\\x-0+6=5\\x+6=5\\x=5-6\\x=-1\end{array}[/latex]
[latex-display](x,y,z)=(-1,0,6)[/latex-display]Example: Solving a System of Three Equations in Three Variables by Elimination
Find a solution to the following system:[latex]\begin{align}x - 2y+3z=9& &\text{(1)} \\ -x+3y-z=-6& &\text{(2)} \\ 2x - 5y+5z=17& &\text{(3)} \end{align}[/latex]
Answer: There will always be several choices as to where to begin, but the most obvious first step here is to eliminate [latex]x[/latex] by adding equations (1) and (2).
[latex]\begin{align}x - 2y+3z&=9\\ -x+3y-z&=-6 \\ \hline y+2z&=3 \end{align}[/latex][latex]\hspace{5mm}\begin{gathered}\text{(1})\\ \text{(2)}\\ \text{(4)}\end{gathered}[/latex]
The second step is multiplying equation (1) by [latex]-2[/latex] and adding the result to equation (3). These two steps will eliminate the variable [latex]x[/latex].[latex]\begin{align}−2x+4y−6z&=−18 \\ 2x−5y+5z&=17 \\ \hline −y−z&=−1\end{align}[/latex][latex]\hspace{5mm}\begin{align}&\text{(2) multiplied by }−2\\&\left(3\right)\\&(5)\end{align}[/latex]
In equations (4) and (5), we have created a new two-by-two system. We can solve for [latex]z[/latex] by adding the two equations.[latex]\begin{align}y+2z&=3 \\ -y-z&=-1 \\ \hline z&=2 \end{align}[/latex][latex]\hspace{5mm}\begin{align}(4)\\(5)\\(6)\end{align}[/latex]
Choosing one equation from each new system, we obtain the upper triangular form:[latex]\begin{align}x - 2y+3z&=9 && \left(1\right) \\ y+2z&=3 && \left(4\right) \\ z&=2 && \left(6\right) \end{align}[/latex]
Next, we back-substitute [latex]z=2[/latex] into equation (4) and solve for [latex]y[/latex].[latex]\begin{align}y+2\left(2\right)&=3 \\ y+4&=3 \\ y&=-1 \end{align}[/latex]
Finally, we can back-substitute [latex]z=2[/latex] and [latex]y=-1[/latex] into equation (1). This will yield the solution for [latex]x[/latex].[latex]\begin{align} x - 2\left(-1\right)+3\left(2\right)&=9\\ x+2+6&=9\\ x&=1\end{align}[/latex]
The solution is the ordered triple [latex]\left(1,-1,2\right)[/latex].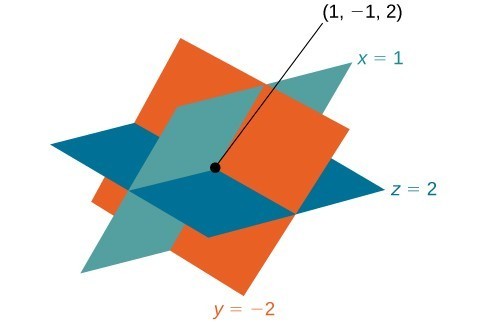
Try It
Solve the system of equations in three variables.[latex]\begin{array}{l}2x+y - 2z=-1\hfill \\ 3x - 3y-z=5\hfill \\ x - 2y+3z=6\hfill \end{array}[/latex]
Answer: [latex-display]\left(1,-1,1\right)[/latex-display]
[embed]Applications of Systems of Three Equations in Three Variables
Now we are ready to handle the problem we encountered as we began this section by using what we know about linear equations to translate the situation into a system of three equations. Then, we'll use our new understanding of three-by-three systems to find the solution.Tip for success
Applications of three-by-three systems are complicated. Work through each of the examples below perhaps more than once or twice. Don't be discouraged if you don't understand the process right away. It will take time and practice to become familiar with it.Example: Solving a Real-World Problem Using a System of Three Equations in Three Variables
In the problem posed at the beginning of the section, John invested his inheritance of $12,000 in three different funds: part in a money-market fund paying 3% interest annually; part in municipal bonds paying 4% annually; and the rest in mutual funds paying 7% annually. John invested $4,000 more in mutual funds than he invested in municipal bonds. The total interest earned in one year was $670. How much did he invest in each type of fund?Answer: To solve this problem, we use all of the information given and set up three equations. First, we assign a variable to each of the three investment amounts:
[latex]\begin{align}&x=\text{amount invested in money-market fund} \\ &y=\text{amount invested in municipal bonds} \\ z&=\text{amount invested in mutual funds} \end{align}[/latex]
The first equation indicates that the sum of the three principal amounts is $12,000.[latex]x+y+z=12{,}000[/latex]
We form the second equation according to the information that John invested $4,000 more in mutual funds than he invested in municipal bonds.[latex]z=y+4{,}000[/latex]
The third equation shows that the total amount of interest earned from each fund equals $670.[latex]0.03x+0.04y+0.07z=670[/latex]
Then, we write the three equations as a system.[latex]\begin{align}x+y+z=12{,}000 \\ -y+z=4{,}000 \\ 0.03x+0.04y+0.07z=670 \end{align}[/latex]
To make the calculations simpler, we can multiply the third equation by 100. Thus,[latex]\begin{align}x+y+z=12{,}000 \hspace{5mm} \left(1\right) \\ -y+z=4{,}000 \hspace{5mm} \left(2\right) \\ 3x+4y+7z=67{,}000 \hspace{5mm} \left(3\right) \end{align}[/latex]
Step 1. Interchange equation (2) and equation (3) so that the two equations with three variables will line up.[latex]\begin{align}x+y+z=12{,}000\hfill \\ 3x+4y +7z=67{,}000 \\ -y+z=4{,}000 \end{align}[/latex]
Step 2. Multiply equation (1) by [latex]-3[/latex] and add to equation (2). Write the result as row 2.[latex]\begin{align}x+y+z=12{,}000 \\ y+4z=31{,}000 \\ -y+z=4{,}000 \end{align}[/latex]
Step 3. Add equation (2) to equation (3) and write the result as equation (3).[latex]\begin{align}x+y+z=12{,}000 \\ y+4z=31{,}000 \\ 5z=35{,}000 \end{align}[/latex]
Step 4. Solve for [latex]z[/latex] in equation (3). Back-substitute that value in equation (2) and solve for [latex]y[/latex]. Then, back-substitute the values for [latex]z[/latex] and [latex]y[/latex] into equation (1) and solve for [latex]x[/latex].[latex]\begin{align}&5z=35{,}000 \\ &z=7{,}000 \\ \\ &y+4\left(7{,}000\right)=31{,}000 \\ &y=3{,}000 \\ \\ &x+3{,}000+7{,}000=12{,}000 \\ &x=2{,}000 \end{align}[/latex]
John invested $2,000 in a money-market fund, $3,000 in municipal bonds, and $7,000 in mutual funds.Try It
[embed]Example
Andrea sells photographs at art fairs. She prices the photos according to size: small photos cost [latex]$10[/latex], medium photos cost [latex]$15[/latex], and large photos cost [latex]$40[/latex]. She usually sells as many small photos as medium and large photos combined. She also sells twice as many medium photos as large. A booth at the art fair costs [latex]$300[/latex]. If her sales go as usual, how many of each size photo must she sell to pay for the booth?Answer: To set up the system, first choose the variables. In this case the unknown values are the number of small, medium, and large photos. S = number of small photos sold M = number of medium photos sold L = number of large photos sold The total of her sales must be [latex]$300[/latex] to pay for the booth. We can find the total by multiplying the cost for each size by the number of that size sold. [latex]10[/latex]S = money received for small photos [latex]15[/latex]M = money received for medium photos [latex]40[/latex]L = money received for large photos
Total Sales:[latex]10[/latex]S +[latex]15[/latex]M +[latex]40[/latex]L =[latex]300[/latex]
The number of small photos is the same as the total of medium and large photos combined.S = M + L
She sells twice as many medium photos as large photos.M =[latex]2[/latex]L
To make things easier, rewrite the equations to be in the same format, with all variables on the left side of the equal sign and only a constant number on the right.[latex]\begin{cases}10S+15M+40L=300\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,S–M–L=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M–2L=0\end{cases}[/latex]
Now solve the system. Step 1: First choose two equations and eliminate a variable. Since one equation has no S variable, it may be helpful to use the other two equations and eliminate the S variable from them. Multiply both sides of the second equation by [latex]−10[/latex].[latex]\begin{array}{l}-10(S–M–L)=-10(0)\\-10s+10M+10L=0\end{array}[/latex]
Now add this modified equation with the first equation in the original list of equation.[latex]\begin{array}{ccc}10S+15M+40L=300\\\underline{+(-10s+10M+10L=0)}\\25M+50L=300\end{array}[/latex]
Step 2: The other equation for our two-variable system will be the remaining equation (that has no S variable). Eliminate a second variable using the equation from step [latex]1[/latex]. While you could multiply the third of the original equations by [latex]25[/latex] to eliminate L, the numbers will stay nicer if you divide the resulting equation from step [latex]1[/latex] by [latex]25[/latex]. Do not forget to be careful of the signs! Divide first:[latex]\begin{array}{ccc}\dfrac{25}{25}M+\dfrac{50}{25}L=\dfrac{300}{25}\\M+2L=12\end{array}[/latex]
Now eliminate L by adding M-2L=0 to this new equation.[latex]\begin{array}{l}M+2L=12\\\underline{M–2L=0}\\2M=12\\M=\dfrac{12}{2}=6\end{array}[/latex]
Step 3: Use M=[latex]6[/latex] and one of the equations containing just two variables to solve for the second variable. It is best to use one of the original equation in case an error was made in multiplication.[latex]\begin{array}{ccc}M-2L=0\\6-2L=0\\-2L=-6\\L=3\end{array}[/latex]
Step 4: Use the two found values and one of the original equations to solve for the third variable.
[latex]\begin{array}{ccc}S–M–L=0\\S-6-3=0\\S-9=0\\S=9\end{array}[/latex]
Step 5: Check your answer. With application problems, it is sometimes easier (and better) to use the original wording of the problem rather than the equations you write.
She usually sells as many small photos as medium and large photos combined.- Medium and large photos combined: [latex]6 + 3 = 9[/latex], which is the number of small photos.
- Medium photos is [latex]6[/latex], which is twice the number of large photos [latex](3)[/latex].
- Andrea receives [latex]$10(9)[/latex] or [latex]$90[/latex] for the [latex]9[/latex] small photos, [latex]$15(6)[/latex] or [latex]$90[/latex] for the [latex]6[/latex] medium photos, and [latex]$40(3)[/latex] or [latex]$120[/latex] for the large photos. [latex]$90 + $90 + $120 = $300[/latex].
In the following video example, we show how to define a system of three equations in three variables that represents a mixture needed by a chemist.
https://youtu.be/612Ad0W9ZeY Our last example shows you how to write a system of three equations that represents ticket sales for a theater that has three different prices for tickets. https://youtu.be/Wg_v5R7BFo0Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 23765. Authored by: Shahbazian,Roy. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Systems of Equations in Three Variables: Part 1 of 2 . Authored by: Sousa, James (Mathispower4u.com). License: CC BY: Attribution.
- System of 3 Equations with 3 Unknowns Application - Concentration Problem. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
- System of 3 Equations with 3 Unknowns Application - Ticket Sales. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
