Rates of Change
Learning Outcomes
- Find the average rate of change of a function.
| [latex]y[/latex] | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
| [latex]C\left(y\right)[/latex] | 2.31 | 2.62 | 2.84 | 3.30 | 2.41 | 2.84 | 3.58 | 3.68 |
[latex]\begin{align}\text{Average rate of change} &=\frac{\text{Change in output}}{\text{Change in input}}\\[2mm] &=\frac{\Delta y}{\Delta x}\\[2mm] &=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\\[2mm] &=\frac{f\left({x}_{2}\right)-f\left({x}_{1}\right)}{{x}_{2}-{x}_{1}}\end{align}[/latex]
recall the slope of a line
The formula for the average rate of change of any function looks a lot like the formula for finding the slope of a line. That's because the average rate of change between two points on the graph of a function is the slope of the straight line between those points. Since [latex]y=f(x), \, \text{we write} \, \left(x,y\right) \, \text{as} \, \left(x, f(x)\right) \, \text{and} \, \dfrac{\text{rise}}{\text{run}}\Rightarrow \dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}} \Rightarrow \dfrac{f\left({x}_{2}\right)-f\left({x}_{1}\right)}{{x}_{2}-{x}_{1}}. [/latex][latex]\dfrac{\Delta y}{\Delta x}=\dfrac{{1.37}}{\text{7 years}}\approx 0.196\text{ dollars per year}[/latex]
On average, the price of gas increased by about 19.6¢ each year. Other examples of rates of change include:- A population of rats increasing by 40 rats per week
- A car traveling 68 miles per hour (distance traveled changes by 68 miles each hour as time passes)
- A car driving 27 miles per gallon of gasoline (distance traveled changes by 27 miles for each gallon)
- The current through an electrical circuit increasing by 0.125 amperes for every volt of increased voltage
- The amount of money in a college account decreasing by $4,000 per quarter
A General Note: Rate of Change
A rate of change describes how an output quantity changes relative to the change in the input quantity. The units on a rate of change are "output units per input units." The average rate of change between two input values is the total change of the function values (output values) divided by the change in the input values.[latex]\dfrac{\Delta y}{\Delta x}=\dfrac{f\left({x}_{2}\right)-f\left({x}_{1}\right)}{{x}_{2}-{x}_{1}}[/latex]
How To: Given the value of a function at different points, calculate the average rate of change of a function for the interval between two values [latex]{x}_{1}[/latex] and [latex]{x}_{2}[/latex].
- Calculate the difference [latex]{y}_{2}-{y}_{1}=\Delta y[/latex].
- Calculate the difference [latex]{x}_{2}-{x}_{1}=\Delta x[/latex].
- Find the ratio [latex]\dfrac{\Delta y}{\Delta x}[/latex].
Example: Computing an Average Rate of Change
Using the data in the table below, find the average rate of change of the price of gasoline between 2007 and 2009.| [latex]y[/latex] | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
| [latex]C\left(y\right)[/latex] | 2.31 | 2.62 | 2.84 | 3.30 | 2.41 | 2.84 | 3.58 | 3.68 |
Answer: In 2007, the price of gasoline was $2.84. In 2009, the cost was $2.41. The average rate of change is
[latex]\begin{align}\frac{\Delta y}{\Delta x}&=\dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\\[2mm]&=\dfrac{$2.41-$2.84}{2009 - 2007}\\[2mm]&=\dfrac{-$0.43}{2\text{ years}}\\[2mm]&={-$0.22}\text{ per year}\end{align}[/latex]
Analysis of the Solution
Note that a decrease is expressed by a negative change or "negative increase." A rate of change is negative when the output decreases as the input increases or when the output increases as the input decreases.Try It
Using the data in the table below, find the average rate of change between 2005 and 2010.| [latex]y[/latex] | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
| [latex]C\left(y\right)[/latex] | 2.31 | 2.62 | 2.84 | 3.30 | 2.41 | 2.84 | 3.58 | 3.68 |
Answer:
[latex]\dfrac{$2.84-$2.31}{5\text{ years}}=\dfrac{$0.53}{5\text{ years}}=$0.106[/latex] per year.
[ohm_question]1731[/ohm_question]Example: Computing Average Rate of Change from a Table
After picking up a friend who lives 10 miles away, Anna records her distance from home over time. The values are shown in the table below. Find her average speed over the first 6 hours.| t (hours) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| D(t) (miles) | 10 | 55 | 90 | 153 | 214 | 240 | 282 | 300 |
Answer: Here, the average speed is the average rate of change. She traveled 282 miles in 6 hours, for an average speed of
[latex]\begin{align}\dfrac{292 - 10}{6 - 0}&=\dfrac{282}{6}\\[2mm]&=47 \end{align}[/latex]
The average speed is 47 miles per hour.Analysis of the Solution
Because the speed is not constant, the average speed depends on the interval chosen. For the interval [2,3], the average speed is 63 miles per hour. [ohm_question]74150[/ohm_question]Example: Computing Average Rate of Change from a Graph
Given the function [latex]g\left(t\right)[/latex], find the average rate of change on the interval [latex]\left[-1,2\right][/latex].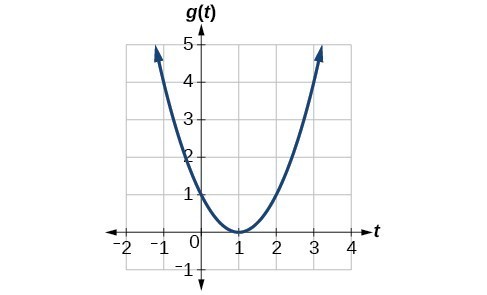
Answer:
 At [latex]t=-1[/latex], the graph shows [latex]g\left(-1\right)=4[/latex]. At [latex]t=2[/latex], the graph shows [latex]g\left(2\right)=1[/latex].
The horizontal change [latex]\Delta t=3[/latex] is shown by the red arrow, and the vertical change [latex]\Delta g\left(t\right)=-3[/latex] is shown by the turquoise arrow. The output changes by –3 while the input changes by 3, giving an average rate of change of
At [latex]t=-1[/latex], the graph shows [latex]g\left(-1\right)=4[/latex]. At [latex]t=2[/latex], the graph shows [latex]g\left(2\right)=1[/latex].
The horizontal change [latex]\Delta t=3[/latex] is shown by the red arrow, and the vertical change [latex]\Delta g\left(t\right)=-3[/latex] is shown by the turquoise arrow. The output changes by –3 while the input changes by 3, giving an average rate of change of
[latex]\dfrac{1 - 4}{2-\left(-1\right)}=\dfrac{-3}{3}=-1[/latex]
Analysis of the Solution
Note that the order we choose is very important. If, for example, we use [latex]\dfrac{{y}_{2}-{y}_{1}}{{x}_{1}-{x}_{2}}[/latex], we will not get the correct answer. Decide which point will be 1 and which point will be 2, and keep the coordinates fixed as [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex]. [ohm_question]16233[/ohm_question]Example: Computing Average Rate of Change for a Function Expressed as a Formula
Compute the average rate of change of [latex]f\left(x\right)={x}^{2}-\frac{1}{x}[/latex] on the interval [latex]\text{[2,}\text{4].}[/latex]Answer: We can start by computing the function values at each endpoint of the interval.
[latex]\begin{align}f(2)&=2^{2}-\frac{1}{2} &\,\,f(4)&=4^{2}-\frac{1}{4}\\[2mm]&=4-\frac{1}{2}&\,\,&=16-\frac{1}{4}\\[2mm]&=\frac{7}{2}&\,\,&=\frac{63}{4}\end{align}[/latex]
Now we compute the average rate of change.[latex]\begin{align}\text{Average rate of change}&=\dfrac{f\left(4\right)-f\left(2\right)}{4 - 2} \\[2mm]&=\dfrac{\frac{63}{4}-\frac{7}{2}}{4 - 2} \\[2mm]&=\dfrac{\frac{49}{4}}{2}\\[2mm]&=\dfrac{49}{8}\end{align}[/latex]
Try It
Find the average rate of change of [latex]f\left(x\right)=x - 2\sqrt{x}[/latex] on the interval [latex]\left[1,9\right][/latex].Answer: [latex-display]\dfrac{1}{2}[/latex-display]
[ohm_question]1732[/ohm_question] [ohm_question]1733[/ohm_question] [ohm_question]111818[/ohm_question]Example: Finding the Average Rate of Change of a Force
The electrostatic force [latex]F[/latex], measured in newtons, between two charged particles can be related to the distance between the particles [latex]d[/latex], in centimeters, by the formula [latex]F\left(d\right)=\frac{2}{{d}^{2}}[/latex]. Find the average rate of change of force if the distance between the particles is increased from 2 cm to 6 cm.Answer: We are computing the average rate of change of [latex]F\left(d\right)=\frac{2}{{d}^{2}}[/latex] on the interval [latex]\left[2,6\right][/latex].
[latex]\begin{align}\text{Average rate of change}&=\dfrac{F\left(6\right)-F\left(2\right)}{6 - 2}\\[2mm]&=\dfrac{\frac{2}{{6}^{2}}-\frac{2}{{2}^{2}}}{6 - 2}&\text{Simplify} \\[2mm]&=\dfrac{\frac{2}{36}-\frac{2}{4}}{4}\\[2mm]&=\dfrac{-\frac{16}{36}}{4}&\text{Combine numerator terms}\\[2mm]&=-\dfrac{1}{9}&\text{Simplify}&\end{align}[/latex]
The average rate of change is [latex]-\frac{1}{9}[/latex] newton per centimeter.Example: Finding an Average Rate of Change as an Expression
Find the average rate of change of [latex]g\left(t\right)={t}^{2}+3t+1[/latex] on the interval [latex]\left[0,a\right][/latex]. The answer will be an expression involving [latex]a[/latex].Answer: We use the average rate of change formula.
[latex]\begin{align}\text{Average rate of change}&=\dfrac{g\left(a\right)-g\left(0\right)}{a - 0}&\text{Evaluate}\\[2mm]&=\dfrac{\left({a}^{2}+3a+1\right)-\left({0}^{2}+3\left(0\right)+1\right)}{a - 0}&\text{Simplify}\\[2mm]&=\dfrac{{a}^{2}+3a+1 - 1}{a}&\text{Simplify and factor}\\[2mm]&=\dfrac{a\left(a+3\right)}{a}&\text{Divide by the common factor }a\\[2mm]&=a+3\end{align}[/latex]
This result tells us the average rate of change in terms of [latex]a[/latex] between [latex]t=0[/latex] and any other point [latex]t=a[/latex]. For example, on the interval [latex]\left[0,5\right][/latex], the average rate of change would be [latex]5+3=8[/latex].Try It
Find the average rate of change of [latex]f\left(x\right)={x}^{2}+2x - 8[/latex] on the interval [latex]\left[5,a\right][/latex].Answer: [latex]a+7[/latex]
[ohm_question]4083[/ohm_question] [ohm_question]15285[/ohm_question]Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 111818. Authored by: LumenLearning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- Ex: Find the Average Rate of Change From a Table - Temperatures. Authored by: Mathispower4u. License: All Rights Reserved. License terms: Standard YouTube LIcense.
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 1731, 1732, 1733, 4083. Authored by: Lippman,David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 74150. Authored by: nearing,Daniel, mb Nearing,Daniel, mb Meacham,William. License: CC BY: Attribution.
- Question ID 16233. Authored by: Sousa,James, mb Lippman,David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
