Identify Functions Using Graphs
Learning Outcomes
- Verify a function using the vertical line test
- Verify a one-to-one function with the horizontal line test
- Identify the graphs of the toolkit functions
 The vertical line test can be used to determine whether a graph represents a function. A vertical line includes all points with a particular [latex]x[/latex] value. The [latex]y[/latex] value of a point where a vertical line intersects a graph represents an output for that input [latex]x[/latex] value. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because that [latex]x[/latex] value has more than one output. A function has only one output value for each input value.
The vertical line test can be used to determine whether a graph represents a function. A vertical line includes all points with a particular [latex]x[/latex] value. The [latex]y[/latex] value of a point where a vertical line intersects a graph represents an output for that input [latex]x[/latex] value. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because that [latex]x[/latex] value has more than one output. A function has only one output value for each input value.
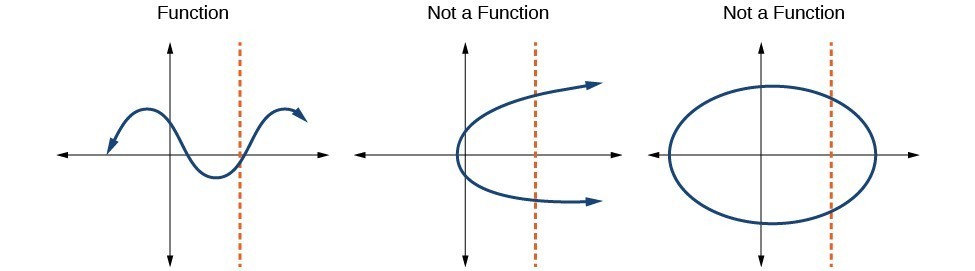
How To: Given a graph, use the vertical line test to determine if the graph represents a function.
- Inspect the graph to see if any vertical line drawn would intersect the curve more than once.
- If there is any such line, the graph does not represent a function.
- If no vertical line can intersect the curve more than once, the graph does represent a function.
Example: Applying the Vertical Line Test
Which of the graphs represent(s) a function [latex]y=f\left(x\right)?[/latex]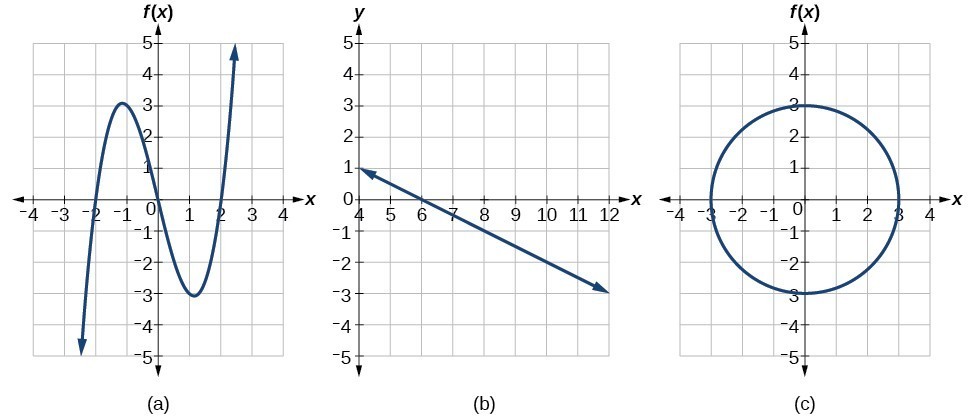
Answer:
If any vertical line intersects a graph more than once, the relation represented by the graph is not a function. Notice that any vertical line would pass through only one point of the two graphs shown in parts (a) and (b) of the graph above. From this we can conclude that these two graphs represent functions. The third graph does not represent a function because, at most x-values, a vertical line would intersect the graph at more than one point.
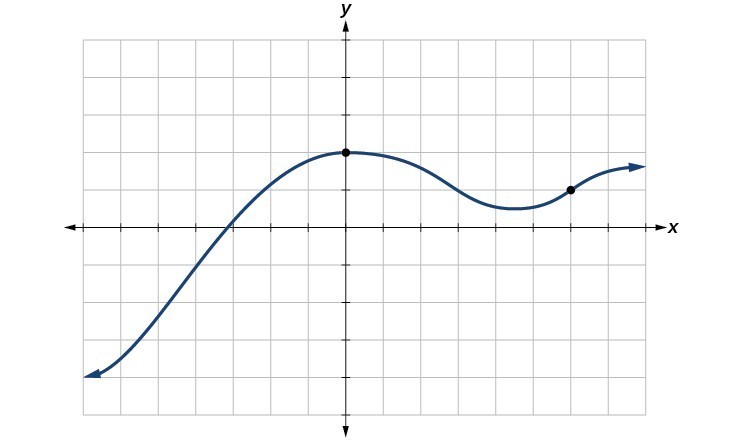
Try It
Does the graph below represent a function?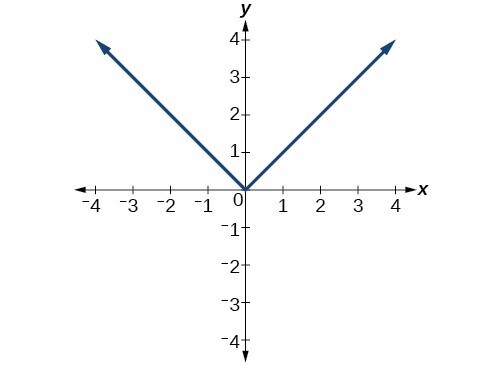
Answer: Yes.
[ohm_question]40676[/ohm_question]try it
In the graph below, use the vertical line test to determine which relations are functions and which are not.
The Horizontal Line Test
relations, functions, and one-to-one functions
A relation is a set of ordered pairs, inputs and their corresponding outputs, [latex]\left(x, y\right)[/latex]. A function is a particular relation in which each input corresponds to exactly one output, [latex]\left(x, f(x)\right)[/latex]. A one-to-one function is a particular function in which each output corresponds to exactly one input.How To: Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function.
- Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
- If there is any such line, the function is not one-to-one.
- If no horizontal line can intersect the curve more than once, the function is one-to-one.
Example: Applying the Horizontal Line Test
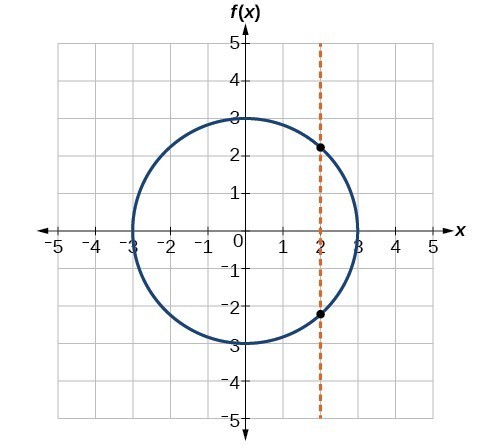
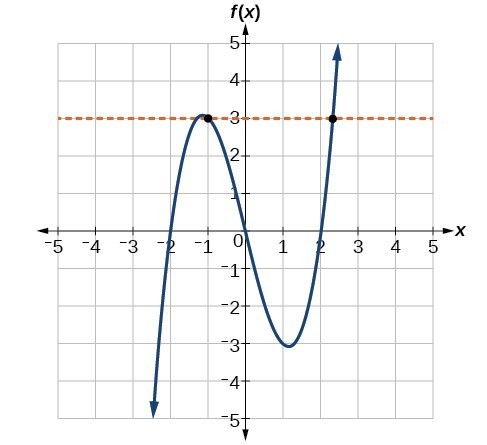
Consider the functions (a), and (b)shown in the graphs below. Are either of the functions one-to-one?
Are either of the functions one-to-one?
Answer:
The function in (a) is not one-to-one. The horizontal line shown below intersects the graph of the function at two points (and we can even find horizontal lines that intersect it at three points.)
 The function in (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once.
The function in (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once.
Identifying Basic Toolkit Functions
toolkit functions
You should memorize the shapes of these graphs along with their names in words and in equation form. Be able to plot a few points of each to the left and right of the y-axis. You'll be using these function families throughout the rest of the course.| Toolkit Functions | ||
|---|---|---|
| Name | Function | Graph |
| Constant | [latex]f\left(x\right)=c[/latex], where [latex]c[/latex] is a constant | 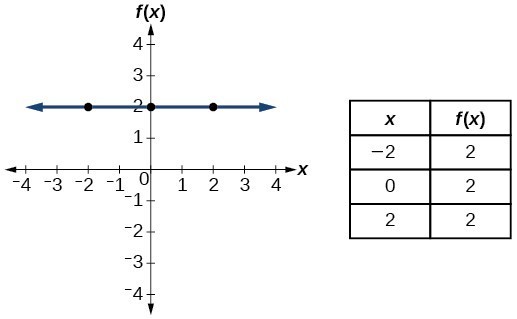 |
| Identity | [latex]f\left(x\right)=x[/latex] |  |
| Absolute value | [latex]f\left(x\right)=|x|[/latex] | 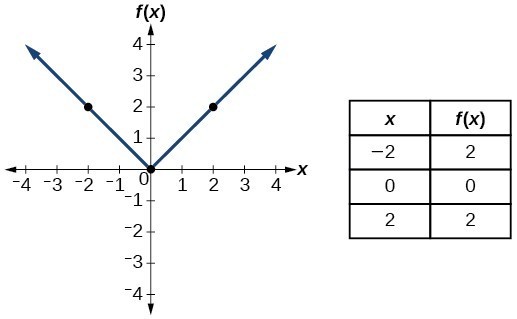 |
| Quadratic | [latex]f\left(x\right)={x}^{2}[/latex] |  |
| Cubic | [latex]f\left(x\right)={x}^{3}[/latex] | 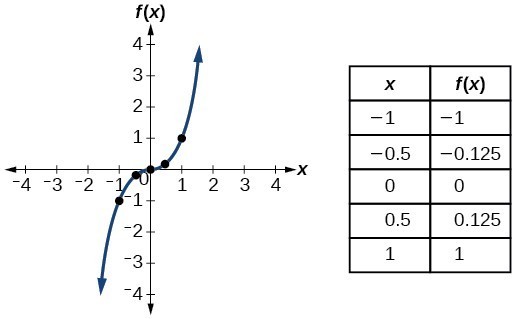 |
| Reciprocal/ Rational | [latex]f\left(x\right)=\frac{1}{x}[/latex] | 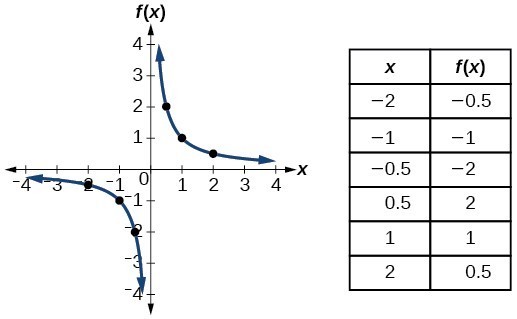 |
| Reciprocal / Rational squared | [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex] | 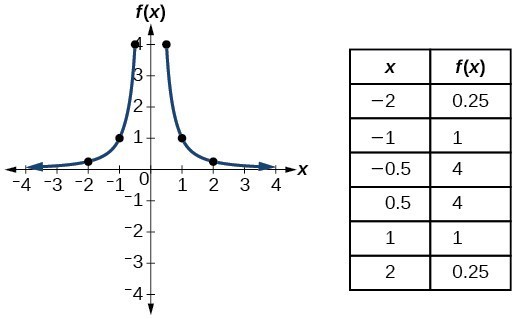 |
| Square root | [latex]f\left(x\right)=\sqrt{x}[/latex] | 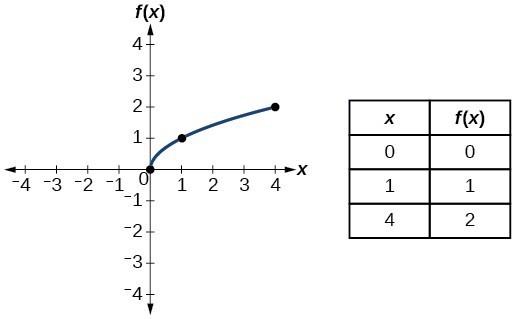 |
| Cube root | [latex]f\left(x\right)=\sqrt[3]{x}[/latex] | 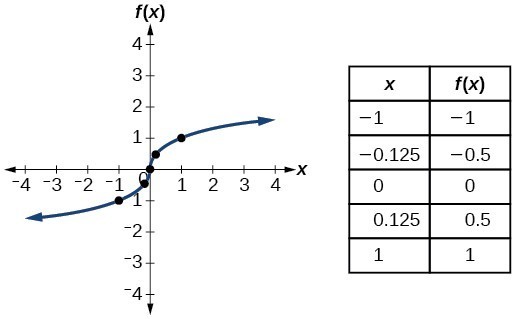 |
Try It
[ohm_question]111722[/ohm_question]Try It
In this exercise, you will reference the nine toolkit functions presented above.- Graph each toolkit function using function notation on an online graphing calculator.
- Make a table of values that references the function and includes at least the interval [-5,5].
Licenses & Attributions
CC licensed content, Original
- Question ID 111715, 11722. Provided by: Lumen Learning License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Vertical Line Test. Authored by: Lumen Learning. Located at: https://www.desmos.com/calculator/dcq8twow2q. License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 40676. Authored by: Jenck, Michael. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
