We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra CoRequisite Course

Graph Solutions to Systems of Linear Inequalities

Learning Outcomes

  • Solve systems of linear inequalities by graphing the solution region
  • Graph solutions to a system that contains a compound inequality
We will continue to practice graphing the solution region for systems of linear inequalities. We will also graph the solutions to a system that includes a compound inequality.

Example

Shade the region of the graph that represents solutions for both inequalities. [latex]x+y\geq1[/latex] and [latex]y–x\geq5[/latex].

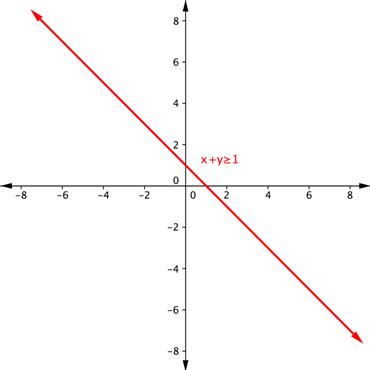Answer: Graph one inequality. First graph the boundary line using a table of values, intercepts, or any other method you prefer. The boundary line for [latex]x+y\geq1[/latex] is [latex]x+y=1[/latex], or [latex]y=−x+1[/latex]. Since the equal sign is included with the greater than sign, the boundary line is solid. A downward-sloping solid line labeled x+y is greater than 1. Find an ordered pair on either side of the boundary line. Insert the x and y-values into the inequality [latex]x+y\geq1[/latex] and see which ordered pair results in a true statement. [latex-display]\begin{array}{r}\text{Test }1:\left(−3,0\right)\\x+y\geq1\\−3+0\geq1\\−3\geq1\\\text{FALSE}\end{array}[/latex-display] [latex-display]\begin{array}{r}\text{Test }2:\left(4,1\right)\\x+y\geq1\\4+1\geq1\\5\geq1\\\text{TRUE}\end{array}[/latex-display] Since [latex](4, 1)[/latex] results in a true statement, the region that includes [latex](4, 1)[/latex] should be shaded. A solid downward-sloping line with the region above it shaded and labeled x+y is greater than or equal to 1. The point (4,1) is in the shaded region. The point (-3,0) is not. 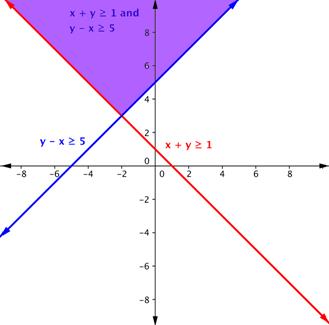Do the same with the second inequality. Graph the boundary line, then test points to find which region is the solution to the inequality. In this case, the boundary line is [latex]y–x=5\left(\text{or }y=x+5\right)[/latex] and is solid. Test point [latex](−3, 0)[/latex] is not a solution of [latex]y–x\geq5[/latex] and test point [latex](0, 6)[/latex] is a solution. A solid blue line with the region above it shaded and labeled y-x is greater than or equal to 5. A solid red line with the region above it shaded and labeled x+y is greater than 1. The point (-3,0) is not in any shaded region. The point (0,6) is in the overlapping shaded region. The purple region in this graph shows the set of all solutions of the system. The previous graph, with the purple overlapping shaded region labeled x+y is greater than or equal to 1 and y-x is greater than or equal to 5.

The videos that follow show more examples of graphing the solution set of a system of linear inequalities. https://youtu.be/ACTxJv1h2_c https://youtu.be/cclH2h1NurM The system in our last example includes a compound inequality.  We will see that you can treat a compound inequality like two lines when you are graphing them.

Example

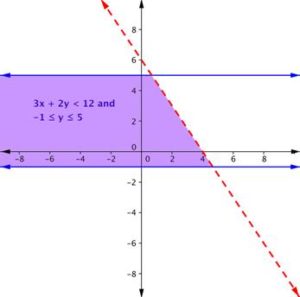
Find the solution to the system [latex] 3x + 2y < 12 [/latex] and [latex] -1 ≤ y ≤ 5 [/latex].

Answer: Graph one inequality. First graph the boundary line, then test points. Remember, because the inequality [latex] 3x + 2y < 12 [/latex] does not include the equal sign, draw a dashed border line. Testing a point like [latex](0, 0)[/latex] will show that the area below the line is the solution to this inequality. image021 The inequality [latex] -1 ≤ y ≤ 5[/latex] is actually two inequalities: [latex]−1 ≤ y[/latex], and [latex]y ≤ 5[/latex]. Another way to think of this is y must be between [latex]−1[/latex] and [latex]5[/latex]. The border lines for both are horizontal. The region between those two lines contains the solutions of [latex] -1 ≤ y ≤ 5[/latex]. We make the lines solid because we also want to include [latex]y = −1 [/latex] and [latex] y = 5[/latex]. Graph this region on the same axes as the other inequality. image022 The purple region shows the set of all solutions of the system. image023

In the video that follows, we show how to solve another system of inequalities that contains a compound inequality. https://youtu.be/ACTxJv1h2_c

Licenses & Attributions

CC licensed content, Original

  • Ex 1: Graph a System of Linear Inequalities. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.

CC licensed content, Shared previously

  • Ex 2: Graph a System of Linear Inequalities. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Determine the Solution to a System of Inequalities (Compound). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.