We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra CoRequisite Course

Domain and Its Effect on Vertical Asymptotes

Learning Outcomes

  • Define the domain of a rational function given an equation.
  • Use the domain of a rational function to define vertical asymptotes.
A vertical asymptote represents a value at which a rational function is undefined, so that value is not in the domain of the function. A reciprocal function (a special case of a rational function) cannot have values in its domain that cause the denominator to equal zero. In general, to find the domain of a rational function, we need to determine which inputs would cause division by zero.

A General Note: Domain of a Rational Function

The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.

How To: Given a rational function, find the domain.

  1. Set the denominator equal to zero.
  2. Solve to find the values of the variable that cause the denominator to equal zero.
  3. The domain contains all real numbers except those found in Step 2.

Example: Finding the Domain of a Rational Function

Find the domain of [latex]f\left(x\right)=\dfrac{x+3}{{x}^{2}-9}[/latex].

Answer: Begin by setting the denominator equal to zero and solving.

[latex]\begin{align} {x}^{2}-9&=0 \\ {x}^{2}&=9 \\ x&=\pm 3 \end{align}[/latex]

The denominator is equal to zero when [latex]x=\pm 3[/latex]. The domain of the function is all real numbers except [latex]x=\pm 3[/latex].

Analysis of the Solution

A graph of this function confirms that the function is not defined when [latex]x=\pm 3[/latex].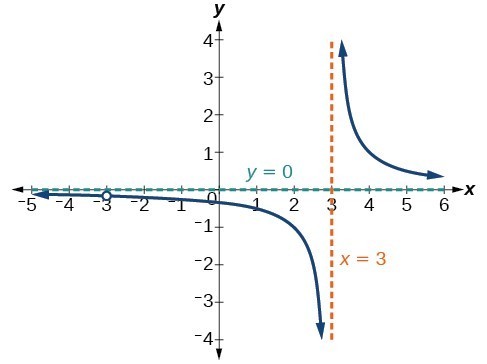 Graph of f(x)=1/(x-3) with its vertical asymptote at x=3 and its horizontal asymptote at y=0. There is a vertical asymptote at [latex]x=3[/latex] and a hole in the graph at [latex]x=-3[/latex]. We will discuss these types of holes in greater detail later in this section.

recall equation solving techniques

We have learned several techniques that will enable us to solve for values of the denominator that cause it to equal zero. Techniques for solving linear and quadratic equations will help you find the domain of most of the rational functions you'll encounter. In the example above, solving for the values that cause [latex]x^2-9=0[/latex] can be found either by factoring or by the square root property. The denominator may also be presented in factored form, as in the example below. In this case, part of the work has already been done, and you can use the zero-product principle to find the zeros of the equation. For example,

If           [latex](x-a)(x-c)=0,[/latex]

then      [latex]x-a=0 \qquad [/latex] or [latex]\qquad x-c=0[/latex]

and       [latex]x=a \qquad[/latex] or [latex]\qquad x=c[/latex].

You may also use the quadratic formula to solve equations in the form of [latex]ax^2+bx+c=0[/latex]. Rational functions can also have more complicated denominators, containing radicals or degrees greater than 2. In each case, equation solving techniques you've seen in the course will apply.

Try It

Find the domain of [latex]f\left(x\right)=\dfrac{4x}{5\left(x - 1\right)\left(x - 5\right)}[/latex].

Answer: The domain is all real numbers except [latex]x=1[/latex] and [latex]x=5[/latex].

[embed]
By looking at the graph of a rational function, we can investigate its local behavior and easily see whether there are asymptotes. We may even be able to approximate their location. Even without the graph, however, we can still determine whether a given rational function has any asymptotes, and calculate their location. Watch the following video to see more examples of finding the domain of a rational function. https://youtu.be/v0IhvIzCc_I

Vertical Asymptotes

The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. Vertical asymptotes occur at the zeros of such factors.

How To: Given a rational function, identify any vertical asymptotes of its graph.

  1. Factor the numerator and denominator.
  2. Note any restrictions in the domain of the function.
  3. Reduce the expression by canceling common factors in the numerator and the denominator.
  4. Note any values that cause the denominator to be zero in this simplified version. These are where the vertical asymptotes occur.
  5. Note any restrictions in the domain where asymptotes do not occur. These are removable discontinuities.

Example: Identifying Vertical Asymptotes

Find the vertical asymptotes of the graph of [latex]k\left(x\right)=\dfrac{5+2{x}^{2}}{2-x-{x}^{2}}[/latex].

Answer: First, factor the numerator and denominator.

[latex]\begin{align}k\left(x\right)&=\dfrac{5+2{x}^{2}}{2-x-{x}^{2}} \\[1mm] &=\dfrac{5+2{x}^{2}}{\left(2+x\right)\left(1-x\right)} \end{align}[/latex]

To find the vertical asymptotes, we determine where this function will be undefined by setting the denominator equal to zero:

[latex]\left(2+x\right)\left(1-x\right)=0[/latex]

[latex]x=-2,1[/latex]

Neither [latex]x=-2[/latex] nor [latex]x=1[/latex] are zeros of the numerator, so the two values indicate two vertical asymptotes. The graph below confirms the location of the two vertical asymptotes.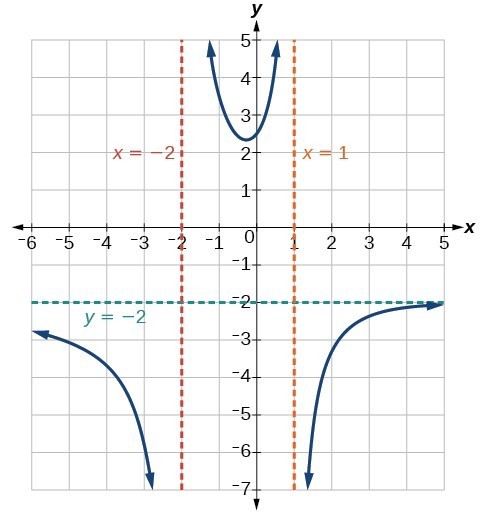 Graph of k(x)=(5+2x)^2/(2-x-x^2) with its vertical asymptotes at x=-2 and x=1 and its horizontal asymptote at y=-2.

Try it

[embed]

Removable Discontinuities

Occasionally, a graph will contain a hole: a single point where the graph is not defined, indicated by an open circle. We call such a hole a removable discontinuity. For example, the function [latex]f\left(x\right)=\dfrac{{x}^{2}-1}{{x}^{2}-2x - 3}[/latex] may be re-written by factoring the numerator and the denominator.

[latex]f\left(x\right)=\dfrac{\left(x+1\right)\left(x - 1\right)}{\left(x+1\right)\left(x - 3\right)}[/latex]

Notice that [latex]x+1[/latex] is a common factor to the numerator and the denominator. The zero of this factor, [latex]x=-1[/latex], is the location of the removable discontinuity. Notice also that [latex]x - 3[/latex] is not a factor in both the numerator and denominator. The zero of this factor, [latex]x=3[/latex], is the vertical asymptote.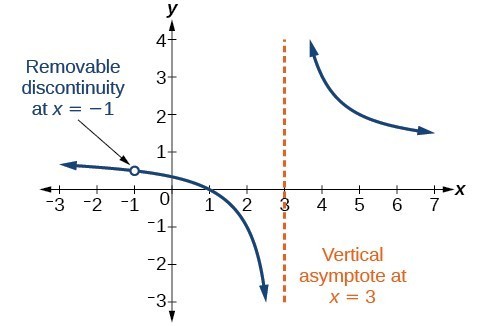 Graph of f(x)=(x^2-1)/(x^2-2x-3) with its vertical asymptote at x=3 and a removable discontinuity at x=-1.

A General Note: Removable Discontinuities of Rational Functions

A removable discontinuity occurs in the graph of a rational function at [latex]x=a[/latex] if a is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value.

Example: Identifying Vertical Asymptotes and Removable Discontinuities for a Graph

Find the vertical asymptotes and removable discontinuities of the graph of [latex]k\left(x\right)=\dfrac{x - 2}{{x}^{2}-4}[/latex].

Answer: Factor the numerator and the denominator.

[latex]k\left(x\right)=\dfrac{x - 2}{\left(x - 2\right)\left(x+2\right)}[/latex]

Notice that there is a common factor in the numerator and the denominator, [latex]x - 2[/latex]. The zero for this factor is [latex]x=2[/latex]. This is the location of the removable discontinuity. Notice that there is a factor in the denominator that is not in the numerator, [latex]x+2[/latex]. The zero for this factor is [latex]x=-2[/latex]. The vertical asymptote is [latex]x=-2[/latex].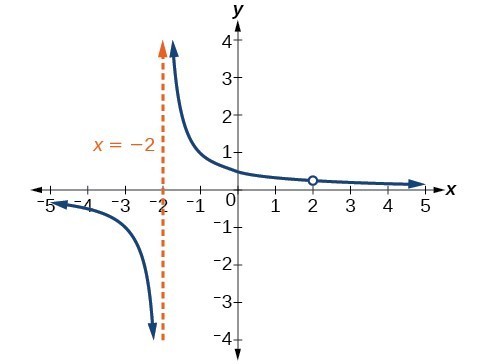 Graph of k(x)=(x-2)/(x-2)(x+2) with its vertical asymptote at x=-2 and a removable discontinuity at x=2. The graph of this function will have the vertical asymptote at [latex]x=-2[/latex], but at [latex]x=2[/latex] the graph will have a hole.

Try It

The rational function [latex]f\left(x\right)\ =\ \dfrac{\left(x^2-a^2\right)}{\left(x^3-\left(a+1\right)x^2+ax\right)}[/latex] needs to be graphed using an online graphing calculator. Investigate the changes in the graph for values of [latex]a[/latex] on the interval [latex][-5,5][/latex], and answer the following questions.
  1. For what values of [latex]a[/latex] does [latex]f(a)[/latex] represent a removable discontinuity?
  2. For what values of [latex]a[/latex] does the line  [latex]x = a[/latex] represent a vertical asymptote?

Answer: Removable discontinuity for values of [latex]a[/latex] on the interval [latex][2,5][/latex] and on the interval [latex][-5,0][/latex], because the vertical line crosses the graph.  Vertical asymptote for [latex]a=1[/latex], because the vertical line [latex]x=1[/latex] coincides with a vertical asymptote.

[ohm_question]74565[/ohm_question]
 

Licenses & Attributions

CC licensed content, Original

  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
  • Domain and It's Affect on Vertical Asymptotes. Authored by: Lumen Learning (with Desmos). Located at: https://www.desmos.com/calculator/sxxheguz0j. License: CC BY: Attribution.

CC licensed content, Shared previously

  • Question ID 74565. Authored by: Nearing,Daniel, mb Lippman,David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Ex: The Domain of Rational Functions . Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.