Distance in the Coordinate Plane
Learning Outcomes
- Use the distance formula to find the distance between two points in the plane.
- Use the midpoint formula to find the midpoint between two points.
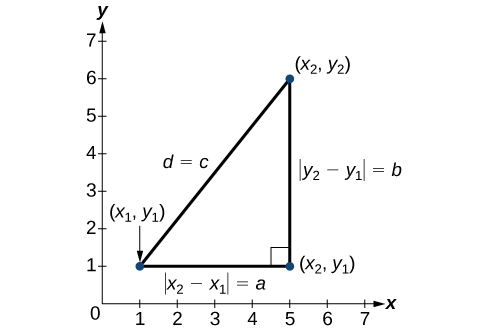The relationship of sides [latex]|{x}_{2}-{x}_{1}|[/latex] and [latex]|{y}_{2}-{y}_{1}|[/latex] to side d is the same as that of sides a and b to side c. We use the absolute value symbol to indicate that the length is a positive number because the absolute value of any number is positive. (For example, [latex]|-3|=3[/latex]. ) The symbols [latex]|{x}_{2}-{x}_{1}|[/latex] and [latex]|{y}_{2}-{y}_{1}|[/latex] indicate that the lengths of the sides of the triangle are positive. To find the length c, take the square root of both sides of the Pythagorean Theorem.
[latex]{c}^{2}={a}^{2}+{b}^{2}\rightarrow c=\sqrt{{a}^{2}+{b}^{2}}[/latex]
It follows that the distance formula is given as
[latex]{d}^{2}={\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}\to d=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}[/latex]
We do not have to use the absolute value symbols in this definition because any number squared is positive.
A General Note: The Distance Formula
Given endpoints [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the distance between two points is given by[latex]d=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}[/latex]
Example: Finding the Distance between Two Points
Find the distance between the points [latex]\left(-3,-1\right)[/latex] and [latex]\left(2,3\right)[/latex].Answer:
Let us first look at the graph of the two points. Connect the points to form a right triangle.
Then, calculate the length of d using the distance formula.
[latex]\begin{array}{l}d=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}\hfill \\ d=\sqrt{{\left(2-\left(-3\right)\right)}^{2}+{\left(3-\left(-1\right)\right)}^{2}}\hfill \\ =\sqrt{{\left(5\right)}^{2}+{\left(4\right)}^{2}}\hfill \\ =\sqrt{25+16}\hfill \\ =\sqrt{41}\hfill \end{array}[/latex]
Try It
Find the distance between two points: [latex]\left(1,4\right)[/latex] and [latex]\left(11,9\right)[/latex].
Answer: [latex]\sqrt{125}=5\sqrt{5}[/latex]
Try it
In the graph below, you can move the points around the coordinate plane by clicking on them and dragging them. Try it out to see how the distance between them changes. Choose two points and answer the following questions:- Calculate the lengths of the sides of the triangle made by the two points you chose and the corner point connected to them by green dotted lines.
- What parts of the distance formula are these lengths?
Example: Finding the Distance between Two Locations
Let’s return to the situation introduced at the beginning of this section. Tracie set out from Elmhurst, IL to go to Franklin Park. On the way, she made a few stops to do errands. Each stop is indicated by a red dot. Find the total distance that Tracie traveled. Compare this with the distance between her starting and final positions.Answer:
The first thing we should do is identify ordered pairs to describe each position. If we set the starting position at the origin, we can identify each of the other points by counting units east (right) and north (up) on the grid. For example, the first stop is 1 block east and 1 block north, so it is at [latex]\left(1,1\right)[/latex]. The next stop is 5 blocks to the east so it is at [latex]\left(5,1\right)[/latex]. After that, she traveled 3 blocks east and 2 blocks north to [latex]\left(8,3\right)[/latex]. Lastly, she traveled 4 blocks north to [latex]\left(8,7\right)[/latex]. We can label these points on the grid.
Next, we can calculate the distance. Note that each grid unit represents 1,000 feet.
- From her starting location to her first stop at [latex]\left(1,1\right)[/latex], Tracie might have driven north 1,000 feet and then east 1,000 feet, or vice versa. Either way, she drove 2,000 feet to her first stop.
- Her second stop is at [latex]\left(5,1\right)[/latex]. So from [latex]\left(1,1\right)[/latex] to [latex]\left(5,1\right)[/latex], Tracie drove east 4,000 feet.
- Her third stop is at [latex]\left(8,3\right)[/latex]. There are a number of routes from [latex]\left(5,1\right)[/latex] to [latex]\left(8,3\right)[/latex]. Whatever route Tracie decided to use, the distance is the same, as there are no angular streets between the two points. Let’s say she drove east 3,000 feet and then north 2,000 feet for a total of 5,000 feet.
- Tracie’s final stop is at [latex]\left(8,7\right)[/latex]. This is a straight drive north from [latex]\left(8,3\right)[/latex] for a total of 4,000 feet.
| From/To | Number of Feet Driven |
|---|---|
| [latex]\left(0,0\right)[/latex] to [latex]\left(1,1\right)[/latex] | 2,000 |
| [latex]\left(1,1\right)[/latex] to [latex]\left(5,1\right)[/latex] | 4,000 |
| [latex]\left(5,1\right)[/latex] to [latex]\left(8,3\right)[/latex] | 5,000 |
| [latex]\left(8,3\right)[/latex] to [latex]\left(8,7\right)[/latex] | 4,000 |
| Total | 15,000 |
[latex]\begin{array}{l}d=\sqrt{{\left(8 - 0\right)}^{2}+{\left(7 - 0\right)}^{2}}\hfill \\ =\sqrt{64+49}\hfill \\ =\sqrt{113}\hfill \\ =10.63\text{ units}\hfill \end{array}[/latex]
At 1,000 feet per grid unit, the distance between Elmhurst, IL to Franklin Park is 10,630.14 feet, or 2.01 miles. The distance formula results in a shorter calculation because it is based on the hypotenuse of a right triangle, a straight diagonal from the origin to the point [latex]\left(8,7\right)[/latex]. Perhaps you have heard the saying "as the crow flies," which means the shortest distance between two points because a crow can fly in a straight line even though a person on the ground has to travel a longer distance on existing roadways.
Using the Midpoint Formula
When the endpoints of a line segment are known, we can find the point midway between them. This point is known as the midpoint and the formula is known as the midpoint formula. Given the endpoints of a line segment, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the midpoint formula states how to find the coordinates of the midpoint [latex]M[/latex].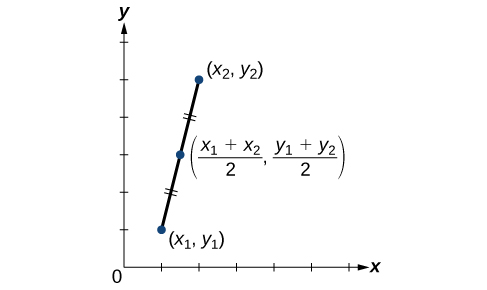[latex]M=\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2}\right)[/latex]
A graphical view of a midpoint is shown below. Notice that the line segments on either side of the midpoint are congruent.
Example: Finding the Midpoint of the Line Segment
Find the midpoint of the line segment with the endpoints [latex]\left(7,-2\right)[/latex] and [latex]\left(9,5\right)[/latex].Answer: Use the formula to find the midpoint of the line segment.
[latex]\begin{array}{l}\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2}\right)\hfill&=\left(\frac{7+9}{2},\frac{-2+5}{2}\right)\hfill \\ \hfill&=\left(8,\frac{3}{2}\right)\hfill \end{array}[/latex]
Try It
Find the midpoint of the line segment with endpoints [latex]\left(-2,-1\right)[/latex] and [latex]\left(-8,6\right)[/latex].Answer: [latex]\left(-5,\frac{5}{2}\right)[/latex]
Example: Finding the Center of a Circle
The diameter of a circle has endpoints [latex]\left(-1,-4\right)[/latex] and [latex]\left(5,-4\right)[/latex]. Find the center of the circle.Answer: The center of a circle is the center or midpoint of its diameter. Thus, the midpoint formula will yield the center point.
[latex]\begin{array}{l}\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2}\right)\\ \left(\frac{-1+5}{2},\frac{-4 - 4}{2}\right)=\left(\frac{4}{2},-\frac{8}{2}\right)=\left(2,-4\right)\end{array}[/latex]
Try It
In the graph below, there is a circle with a diameter whose endpoints are (0,5) and (10,5).- Find the center of the circle.
- Place a point at the center of the circle.
- Now move the endpoints of the diameter by clicking on them and dragging them. Notice that the size and location of the circle changes.
- Now graph the center point of a circle of any radius given that the equation for a circle of any radius with any center [latex](h,k)[/latex] is [latex](x-h)^2+(y-k)^2 = r^2[/latex].
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Midpoint Interactive. Authored by: Lumen Learning. Located at: https://www.desmos.com/calculator/j2blmpiid7. License: CC BY: Attribution.
- Distance in the Plane Interactive. Authored by: Lumen Learning. Located at: https://www.desmos.com/calculator/nrtjcgmy69. License: Public Domain: No Known Copyright.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 19140. Authored by: Amy Lambert. License: CC BY: Attribution. License terms: IMathAS Community License CC- BY + GPL.
- Question ID 2308. Authored by: David Lippman. License: CC BY: Attribution. License terms: IMathAS Community License CC- BY + GPL.
- Question ID 110938. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC- BY + GPL.
- Example: Determine the Distance Between Two Points. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
