Classify a Real Number
Learning Outcomes
- Write integers as rational numbers
- Identify rational numbers
- Classify real numbers into sets
Review for success
About the notation for the sets of numbers we'll explore in this section:- Natural numbers: The most familiar numbers are the natural numbers (sometimes called counting numbers): [latex]1, 2, 3[/latex], and so on. The mathematical symbol for the set of all natural numbers is written as [latex]\mathbb{N}[/latex].
- Whole numbers: The set of whole numbers includes all natural numbers as well as [latex]0[/latex]. There is no special notation for this set.
- Integers: The set of all natural numbers together with their opposites (negative), including 0, is called the set of integers, notated [latex]\mathbb{Z}[/latex].
- Rational numbers: A rational number, [latex]\mathbb{Q}[/latex], is a number that can be expressed as a ratio of integers (a fraction with an integer numerator and a positive, non-zero integer denominator).
- Real numbers: The real numbers include all the numbers above. The symbol for the real numbers is [latex]\mathbb{R}[/latex].
- Irrational numbers: All the real numbers that are not rational are called irrational numbers. These numbers cannot be expressed as a fraction of integers. Irrational numbers can be notated by the symbol [latex]\mathbb{R}\backslash\mathbb{Q}[/latex], that is, the set of all real numbers minus the set of all rational numbers.
[latex]\begin{align}&{\text{negative integers}} && {\text{zero}} && {\text{positive integers}}\\&{\dots ,-3,-2,-1,} && {0,} && {1,2,3,\dots }\\ \text{ }\end{align}[/latex]
The set of rational numbers is written as [latex]\left\{\frac{m}{n}|m\text{ and }{n}\text{ are integers and }{n}\ne{ 0 }\right\}[/latex]. Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never 0. We can also see that every natural number, whole number, and integer is a rational number with a denominator of 1.
Why must the denominator of a quotient never be 0?
Recall that division by zero is undefined.- For any number [latex]a[/latex], [latex]\dfrac{0}{a}=0[/latex]
- For any number [latex]a[/latex], [latex]\dfrac{a}{0}=undefined[/latex]
- a terminating decimal: [latex]\frac{15}{8}=1.875[/latex], or
- a repeating decimal: [latex]\frac{4}{11}=0.36363636\dots =0.\overline{36}[/latex]
Example: Writing Integers as Rational Numbers
Write each of the following as a rational number.- 7
- 0
- –8
Answer: Write a fraction with the integer in the numerator and 1 in the denominator.
- [latex]7=\dfrac{7}{1}[/latex]
- [latex]0=\dfrac{0}{1}[/latex]
- [latex]-8=-\dfrac{8}{1}[/latex]
Try It
Write each of the following as a rational number.- 11
- 3
- –4
Answer:
- [latex]\dfrac{11}{1}[/latex]
- [latex]\dfrac{3}{1}[/latex]
- [latex]-\dfrac{4}{1}[/latex]
Example: Identifying Rational Numbers
Write each of the following rational numbers as either a terminating or repeating decimal.- [latex]-\dfrac{5}{7}[/latex]
- [latex]\dfrac{15}{5}[/latex]
- [latex]\dfrac{13}{25}[/latex]
Answer: Write each fraction as a decimal by dividing the numerator by the denominator.
- [latex]-\dfrac{5}{7}=-0.\overline{714285}[/latex], a repeating decimal
- [latex]\dfrac{15}{5}=3[/latex] (or 3.0), a terminating decimal
- [latex]\dfrac{13}{25}=0.52[/latex], a terminating decimal
Irrational Numbers
At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not 2 or even [latex]\frac{3}{2}[/latex], but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than 3, but still not a rational number. Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers. Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. We can express this symbolically using a particular kind of notation called set notation as [latex]\{h|h \text{is not a rational number\}}[/latex], that is, "the set of all numbers [latex]h[/latex] such that [latex]h[/latex] is not a rational number."Example: Differentiating Rational and Irrational Numbers
Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.- [latex]\sqrt{25}[/latex]
- [latex]\dfrac{33}{9}[/latex]
- [latex]\sqrt{11}[/latex]
- [latex]\dfrac{17}{34}[/latex]
- [latex]0.3033033303333\dots[/latex]
Answer:
- [latex]\sqrt{25}:[/latex] This can be simplified as [latex]\sqrt{25}=5[/latex]. Therefore, [latex]\sqrt{25}[/latex] is rational.
- [latex]\dfrac{33}{9}:[/latex] Because it is a fraction, [latex]\dfrac{33}{9}[/latex] is a rational number. Next, simplify and divide.
[latex]\dfrac{33}{9}=\dfrac{{{11}\cdot{3}}}{{{3}\cdot{3}}}=\dfrac{11}{3}=3.\overline{6}[/latex]So, [latex]\dfrac{33}{9}[/latex] is rational and a repeating decimal.
- [latex]\sqrt{11}:[/latex] This cannot be simplified any further. Therefore, [latex]\sqrt{11}[/latex] is an irrational number.
- [latex]\dfrac{17}{34}:[/latex] Because it is a fraction, [latex]\dfrac{17}{34}[/latex] is a rational number. Simplify and divide.
[latex]\dfrac{17}{34}=\dfrac{{1}\cdot{17}}{{2}\cdot{17}}=\dfrac{1}{2}=0.5[/latex]So, [latex]\dfrac{17}{34}[/latex] is rational and a terminating decimal.
- 0.3033033303333... is not a terminating decimal. Also note that there is no repeating pattern because the group of 3s increases each time. Therefore it is neither a terminating nor a repeating decimal and, hence, not a rational number. It is an irrational number.
Real Numbers
Given any number n, we know that n is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers. As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative. The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as 0, with negative numbers to the left of 0 and positive numbers to the right of 0. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of 0. Any real number corresponds to a unique position on the number line. The converse is also true: each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line.Example: Classifying Real Numbers
Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?- [latex]-\dfrac{10}{3}[/latex]
- [latex]\sqrt{5}[/latex]
- [latex]-\sqrt{289}[/latex]
- [latex]-6\pi[/latex]
- [latex]0.615384615384\dots[/latex]
Answer:
- [latex]-\dfrac{10}{3}[/latex] is negative and rational. It lies to the left of 0 on the number line.
- [latex]\sqrt{5}[/latex] is positive and irrational. It lies to the right of 0.
- [latex]-\sqrt{289}=-\sqrt{{17}^{2}}=-17[/latex] is negative and rational. It lies to the left of 0.
- [latex]-6\pi [/latex] is negative and irrational. It lies to the left of 0.
- [latex]0.615384615384\dots [/latex] is a repeating decimal so it is rational and positive. It lies to the right of 0.
Try It
Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?- [latex]\sqrt{73}[/latex]
- [latex]-11.411411411\dots [/latex]
- [latex]\dfrac{47}{19}[/latex]
- [latex]-\dfrac{\sqrt{5}}{2}[/latex]
- [latex]6.210735[/latex]
Answer:
- positive, irrational; right
- negative, rational; left
- positive, rational; right
- negative, irrational; left
- positive, rational; right
Sets of Numbers as Subsets
Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram.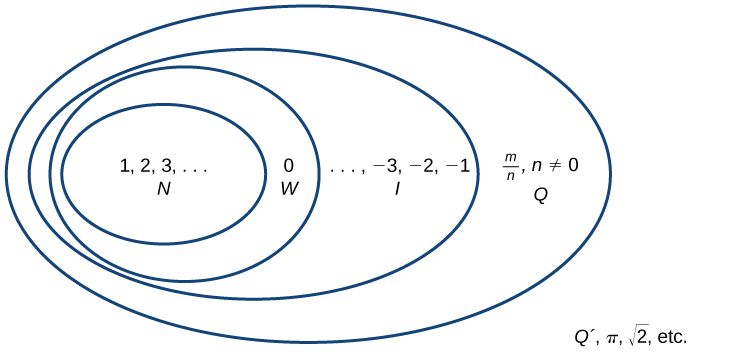 Sets of numbers. N: the set of natural numbers W: the set of whole numbers I: the set of integers Q: the set of rational numbers Q´: the set of irrational numbers
Sets of numbers. N: the set of natural numbers W: the set of whole numbers I: the set of integers Q: the set of rational numbers Q´: the set of irrational numbersA General Note: Sets of Numbers
The set of natural numbers includes the numbers used for counting: [latex]\{1,2,3,\dots\}[/latex]. The set of whole numbers is the set of natural numbers plus zero: [latex]\{0,1,2,3,\dots\}[/latex]. The set of integers adds the negative natural numbers to the set of whole numbers: [latex]\{\dots,-3,-2,-1,0,1,2,3,\dots\}[/latex]. The set of rational numbers includes fractions written as [latex]\{\frac{m}{n}|m\text{ and }n\text{ are integers and }n\ne 0\}[/latex]. The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: [latex]\{h|h\text{ is not a rational number}\}[/latex].Example: Differentiating the Sets of Numbers
Classify each number as being a natural number (N), whole number (W), integer (I), rational number (Q), and/or irrational number (Q').- [latex]\sqrt{36}[/latex]
- [latex]\dfrac{8}{3}[/latex]
- [latex]\sqrt{73}[/latex]
- [latex]-6[/latex]
- [latex]3.2121121112\dots [/latex]
Answer:
| N | W | I | Q | Q` |
| 1. [latex]\sqrt{36}=6[/latex] | X | X | X | X |
| 2. [latex]\dfrac{8}{3}=2.\overline{6}[/latex] | X | |||
| 3. [latex]\sqrt{73}[/latex] | X | |||
| 4. [latex]–6[/latex] | X | X | ||
| 5. [latex]3.2121121112\dots[/latex] | X |
Try It
Classify each number as being a natural number (N), whole number (W), integer (I), rational number (Q), and/or irrational number (Q').- [latex]-\dfrac{35}{7}[/latex]
- [latex]0[/latex]
- [latex]\sqrt{169}[/latex]
- [latex]\sqrt{24}[/latex]
- [latex]4.763763763\dots [/latex]
Answer:
| N | W | I | Q | Q' |
|---|---|---|---|---|
| a. [latex]-\dfrac{35}{7}[/latex] | X | X | ||
| b. 0 | X | X | X | |
| c. [latex]\sqrt{169}[/latex] | X | X | X | X |
| d. [latex]\sqrt{24}[/latex] | X | |||
| e. [latex]4.763763763\dots[/latex] | X |
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Question ID 92383. Authored by: Day, Alyson. License: Other. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 13740. Authored by: Lippman, David. License: Other. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 13741. Authored by: Sousa, James. License: Other. License terms: IMathAS Community License CC-BY + GPL.
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Identifying Sets of Real Numbers . Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
