Characteristics of Functions
Learning Outcomes
- Identify functions given in tabular form.
- Write and evaluate functional relationships using standard notation.
- Determine whether a function is one-to-one.
about the notation
Recall that ordered pairs of the form [latex]\left(x, y\right)[/latex] contain elements from two different sets of values, x-values and y-values. We use curly braces to denote a set of elements. The set of elements named a, b, and c can be written as [latex]\{a, b, c\}[/latex].[latex]\left\{\left(1,2\right),\left(2,4\right),\left(3,6\right),\left(4,8\right),\left(5,10\right)\right\}[/latex]
The domain is [latex]\left\{1,2,3,4,5\right\}[/latex]. The range is [latex]\left\{2,4,6,8,10\right\}[/latex]. Note the values in the domain are also known as an input values, or values of the independent variable, and are often labeled with the lowercase letter [latex]x[/latex]. Values in the range are also known as an output values, or values of the dependent variable, and are often labeled with the lowercase letter [latex]y[/latex]. A function [latex]f[/latex] is a relation that assigns a single value in the range to each value in the domain. In other words, no [latex]x[/latex]-values are used more than once. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, [latex]\left\{1,2,3,4,5\right\}[/latex], is paired with exactly one element in the range, [latex]\left\{2,4,6,8,10\right\}[/latex]. Now let’s consider the set of ordered pairs that relates the terms "even" and "odd" to the first five natural numbers. It would appear as[latex]\left\{\left(\text{odd},1\right),\left(\text{even},2\right),\left(\text{odd},3\right),\left(\text{even},4\right),\left(\text{odd},5\right)\right\}[/latex]
Notice that each element in the domain, [latex]\left\{\text{even,}\text{odd}\right\}[/latex] is not paired with exactly one element in the range, [latex]\left\{1,2,3,4,5\right\}[/latex]. For example, the term "odd" corresponds to three values from the domain, [latex]\left\{1,3,5\right\}[/latex] and the term "even" corresponds to two values from the range, [latex]\left\{2,4\right\}[/latex]. This violates the definition of a function, so this relation is not a function. This image compares relations that are functions and not functions.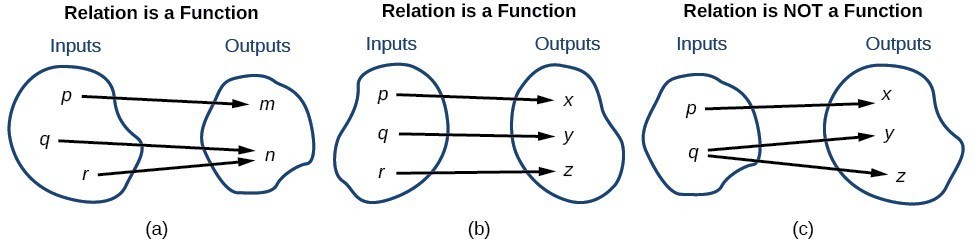 (a) This relationship is a function because each input is associated with a single output. Note that input [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. (b) This relationship is also a function. In this case, each input is associated with a single output. (c) This relationship is not a function because input [latex]q[/latex] is associated with two different outputs.
(a) This relationship is a function because each input is associated with a single output. Note that input [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. (b) This relationship is also a function. In this case, each input is associated with a single output. (c) This relationship is not a function because input [latex]q[/latex] is associated with two different outputs.A General Note: FunctionS
A function is a relation in which each possible input value leads to exactly one output value. We say "the output is a function of the input." The input values make up the domain, and the output values make up the range.How To: Given a relationship between two quantities, determine whether the relationship is a function.
- Identify the input values.
- Identify the output values.
- If each input value leads to only one output value, the relationship is a function. If any input value leads to two or more outputs, the relationship is not a function.
Example: Determining If Menu Price Lists Are Functions
The coffee shop menu consists of items and their prices.- Is price a function of the item?
- Is the item a function of the price?

Answer:
- Let’s begin by considering the input as the items on the menu. The output values are then the prices.
 Each item on the menu has only one price, so the price is a function of the item.
Each item on the menu has only one price, so the price is a function of the item. - Two items on the menu have the same price. If we consider the prices to be the input values and the items to be the output, then the same input value could have more than one output associated with it.
 Therefore, the item is a not a function of price.
Therefore, the item is a not a function of price.
Example: Determining If Class Grade Rules Are Functions
In a particular math class, the overall percent grade corresponds to a grade point average. Is grade point average a function of the percent grade? Is the percent grade a function of the grade point average? The table below shows a possible rule for assigning grade points.| Percent Grade | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
|---|---|---|---|---|---|---|---|---|
| Grade Point Average | 0.0 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Answer: For any percent grade earned, there is an associated grade point average, so the grade point average is a function of the percent grade. In other words, if we input the percent grade, the output is a specific grade point average. In the grading system given, there is a range of percent grades that correspond to the same grade point average. For example, students who receive a grade point average of 3.0 could have a variety of percent grades ranging from 78 all the way to 86. Thus, percent grade is not a function of grade point average.
Try It
The table below lists the five greatest baseball players of all time in order of rank.| Player | Rank |
|---|---|
| Babe Ruth | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Aaron | 5 |
- Is the rank a function of the player name?
- Is the player name a function of the rank?
Answer:
- yes
- yes. (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)
Using Function Notation
recall function notation
Some of the information in this section may look familiar from the Review for Success: Function Notation and Graphs of Functions. Learning to work with functions is naturally challenging, so it's worth another look at it. Don't be discouraged if the notation feels awkward or difficult to understand. Learning mathematics is very similar to learning a new language; it's normal that it takes lots of repetition before it starts to feel natural.[latex]\begin{align}&h\text{ is }f\text{ of }a &&\text{We name the function }f;\text{ height is a function of age}. \\ &h=f\left(a\right) &&\text{We use parentheses to indicate the function input}\text{. } \\ &f\left(a\right) &&\text{We name the function }f;\text{ the expression is read as }"f\text{ of }a". \end{align}[/latex]
Remember, we can use any letter to name the function; we can use the notation [latex]h\left(a\right)[/latex] to show that [latex]h[/latex] depends on [latex]a[/latex]. The input value [latex]a[/latex] must be put into the function [latex]h[/latex] to get an output value. The parentheses indicate that age is input into the function; they do not indicate multiplication. We can also give an algebraic expression as the input to a function. For example [latex]f\left(a+b\right)[/latex] means "first add [latex]a[/latex] and [latex]b[/latex], and the result is the input for the function [latex]f[/latex]." We must perform the operations in this order to obtain the correct result.A General Note: Function Notation
The notation [latex]y=f\left(x\right)[/latex] defines a function named [latex]f[/latex]. This is read as [latex]"y[/latex] is a function of [latex]x."[/latex] The letter [latex]x[/latex] represents the input value, or independent variable. The letter [latex]y[/latex], or [latex]f\left(x\right)[/latex], represents the output value, or dependent variable.Example: Using Function Notation for Days in a Month
Use function notation to represent a function whose input is the name of a month and output is the number of days in that month.Answer:
The number of days in a month is a function of the name of the month, so if we name the function [latex]f[/latex], we write [latex]\text{days}=f\left(\text{month}\right)[/latex] or [latex]d=f\left(m\right)[/latex]. The name of the month is the input to a "rule" that associates a specific number (the output) with each input.
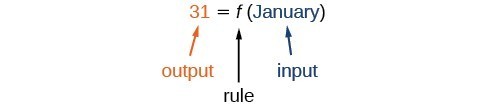 For example, [latex]f\left(\text{April}\right)=30[/latex], because March has 31 days. The notation [latex]d=f\left(m\right)[/latex] reminds us that the number of days, [latex]d[/latex] (the output), is dependent on the name of the month, [latex]m[/latex] (the input).
For example, [latex]f\left(\text{April}\right)=30[/latex], because March has 31 days. The notation [latex]d=f\left(m\right)[/latex] reminds us that the number of days, [latex]d[/latex] (the output), is dependent on the name of the month, [latex]m[/latex] (the input).
Analysis of the Solution
We must restrict the function to non-leap years. Otherwise, February would have 2 outputs and this would not be a function. Also note that the inputs to a function do not have to be numbers; function inputs can be names of people, labels of geometric objects, or any other element that determines some kind of output. However, most of the functions we will work with in this book will have numbers as inputs and outputs.Example: Interpreting Function Notation
A function [latex]N=f\left(y\right)[/latex] gives the number of police officers, [latex]N[/latex], in a town in year [latex]y[/latex]. What does [latex]f\left(2005\right)=300[/latex] represent?Answer: When we read [latex]f\left(2005\right)=300[/latex], we see that the input year is 2005. The value for the output, the number of police officers, [latex]N[/latex], is 300. Remember, [latex]N=f\left(y\right)[/latex]. The statement [latex]f\left(2005\right)=300[/latex] tells us that in the year 2005 there were 300 police officers in the town.
[ohm_question]2510[/ohm_question]Q & A
Instead of a notation such as [latex]y=f\left(x\right)[/latex], could we use the same symbol for the output as for the function, such as [latex]y=y\left(x\right)[/latex], meaning "y is a function of x?" Yes, this is often done, especially in applied subjects that use higher math, such as physics and engineering. However, in exploring math itself we like to maintain a distinction between a function such as [latex]f[/latex], which is a rule or procedure, and the output [latex]y[/latex] we get by applying [latex]f[/latex] to a particular input [latex]x[/latex]. This is why we usually use notation such as [latex]y=f\left(x\right),P=W\left(d\right)[/latex], and so on.Representing Functions Using Tables
A common method of representing functions is in the form of a table. The table rows or columns display the corresponding input and output values. In some cases these values represent all we know about the relationship; other times the table provides a few select examples from a more complete relationship. The table below lists the input number of each month (January = 1, February = 2, and so on) and the output value of the number of days in that month. This information represents all we know about the months and days for a given year (that is not a leap year). Note that, in this table, we define a days-in-a-month function [latex]f[/latex], where [latex]D=f\left(m\right)[/latex] identifies months by an integer rather than by name.| Month number, [latex]m[/latex] (input) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Days in month, [latex]D[/latex] (output) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
| [latex]n[/latex] | 1 | 2 | 3 | 4 | 5 |
| [latex]Q[/latex] | 8 | 6 | 7 | 6 | 8 |
| Age in years, [latex]\text{ }a\text{ }[/latex] (input) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Height in inches, [latex]\text{ }h\text{ }[/latex] (output) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
How To: Given a table of input and output values, determine whether the table represents a function.
- Identify the input and output values.
- Check to see if each input value is paired with only one output value. If so, the table represents a function.
reading functions from a table
Note that the tables above indicate which values are the inputs and which are the outputs to make it easier to clearly identify the relationship. Sometimes, though, the relationship is not labeled. For instance, if a table consists of measures of distance in one column and measures of time in another, you might fairly assume that time is the input and that a distance traveled would be dependent upon the time spent traveling. Either way, when reading a function from a table, it's a good idea to try to discern which values are intended to be or make the most sense as the inputs and which make most sense as outcome values, dependent upon the inputs.Example: Identifying Tables that Represent Functions
Which table, A, B, or C, represents a function (if any)?| Table A | |
|---|---|
| Input | Output |
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Table B | |
|---|---|
| Input | Output |
| –3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Table C | |
|---|---|
| Input | Output |
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Answer: a) and b) define functions. In both, each input value corresponds to exactly one output value. c) does not define a function because the input value of 5 corresponds to two different output values. When a table represents a function, corresponding input and output values can also be specified using function notation. The function represented by a) can be represented by writing
[latex]f\left(2\right)=1,f\left(5\right)=3,\text{and }f\left(8\right)=6[/latex]
Similarly, the statements [latex]g\left(-3\right)=5,g\left(0\right)=1,\text{and }g\left(4\right)=5[/latex] represent the function in b). c) cannot be expressed in a similar way because it does not represent a function. [ohm_question]1729[/ohm_question]recall evaluating functions
Since a function [latex]y=f(x)[/latex] is an equation, we can evaluate it for a numerical or algebraic input. Ex. if [latex]f(x)=5x-11[/latex], we can find [latex]f(2)[/latex] or [latex]f(a+b)[/latex].[latex]\begin{align}f(2) &= 5(2) -11 \\ &= 10 - 11 \\ &= -1\end{align}[/latex]
or
[latex]\begin{align}f(a+b) &= 5(a+b)-11 \\ &= 5a + 5b - 11\end{align}[/latex].
Note that we can also solve for what value of the input makes the output a certain value. That is, given our function above, [latex]f(x)=5x-11[/latex], what value of x makes [latex]f(x)=1[/latex]?Answer: The idea is to replace [latex]f(x)[/latex] the value of 1, then solve for the input x that makes that a true statement. [latex-display]\begin{align}f(x) &= 5x-11 \\ 1 &= 5x-11 \\ 12 &= 5x \\ \dfrac{12}{5} &= x\end{align}[/latex-display]
Determine whether a function is one-to-one
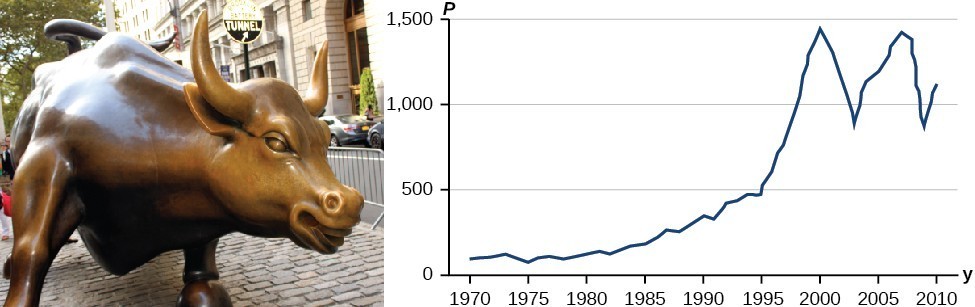 Some functions have a given output value that corresponds to two or more input values. For example, in the following stock chart the stock price was $1000 on five different dates, meaning that there were five different input values that all resulted in the same output value of $1000.
However, some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in.
Some functions have a given output value that corresponds to two or more input values. For example, in the following stock chart the stock price was $1000 on five different dates, meaning that there were five different input values that all resulted in the same output value of $1000.
However, some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in.
| Letter grade | Grade point average |
|---|---|
| A | 4.0 |
| B | 3.0 |
| C | 2.0 |
| D | 1.0 |
 The function in part (a) shows a relationship that is not a one-to-one function because inputs [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. The function in part (b) shows a relationship that is a one-to-one function because each input is associated with a single output.
The function in part (a) shows a relationship that is not a one-to-one function because inputs [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. The function in part (b) shows a relationship that is a one-to-one function because each input is associated with a single output.
A General Note: One-to-One Function
A one-to-one function is a function in which each output value corresponds to exactly one input value.Example: Determining Whether a Relationship Is a One-to-One Function
Is the area of a circle a function of its radius? If yes, is the function one-to-one?Answer: A circle of radius [latex]r[/latex] has a unique area measure given by [latex]A=\pi {r}^{2}[/latex], so for any input, [latex]r[/latex], there is only one output, [latex]A[/latex]. The area is a function of radius [latex]r[/latex]. If the function is one-to-one, the output value, the area, must correspond to a unique input value, the radius. Any area measure [latex]A[/latex] is given by the formula [latex]A=\pi {r}^{2}[/latex]. Because areas and radii are positive numbers, there is exactly one solution: [latex]r=\sqrt{\frac{A}{\pi }}[/latex]. So the area of a circle is a one-to-one function of the circle’s radius.
recall manipulating formulas to isolate a certain variable
In the example above, a formula was solved for one of the variables. We often need to do this in order to rewrite the formula in a useful way.Answer: In the example above, the formula for the area of a circle, [latex]A=\pi {r}^{2}[/latex], was solved for A using the properties of equality. [latex-display]\begin{align}A &= \pi {r}^{2} \\ \dfrac{A}{\pi} &= r^2 \quad \text{divide both sides by }\pi \\ r &= \sqrt{\frac{A}{\pi }} \quad \text{ take the square root of both sides}\end{align}[/latex-display] Only the positive root was required since radius cannot be negative.
Try It
- Is a balance a function of the bank account number?
- Is a bank account number a function of the balance?
- Is a balance a one-to-one function of the bank account number?
Answer:
- yes, because each bank account (input) has a single balance (output) at any given time.
- no, because several bank accounts (inputs) may have the same balance (output).
- no, because the more than one bank account (input) can have the same balance (output).
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 111625. Provided by: Lumen Learning License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- Determine if a Relation is a Function. Authored by: James Sousa. License: All Rights Reserved. License terms: Standard YouTube License.
- Function Notation Application. Authored by: James Sousa. License: CC BY: Attribution.
- Function Notation Application. Authored by: James Sousa. License: CC BY: Attribution.
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 2510, 1729. Authored by: Lippman, David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 15800. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
