We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra CoRequisite Course

Arithmetic Series

Learning Outcomes

  • Evaluate a sum given in summation notation.
  • Find the partial sum of an arithmetic series.
  • Solve an application problem using an arithmetic series.

Using Summation Notation

To find the total amount of money in the college fund and the sum of the amounts deposited, we need to add the amounts deposited each month and the amounts earned monthly. The sum of the terms of a sequence is called a series. Consider, for example, the following series.

[latex]3+7+11+15+19+\cdots[/latex]

The [latex]n\text{th }[/latex] partial sum of a series is the sum of a finite number of consecutive terms beginning with the first term. The notation

[latex]\begin{align}&{S}_{n}\text{ represents the partial sum.} \\ &{S}_{1}=3 \\ &{S}_{2}=3+7=10 \\ &{S}_{3}=3+7+11=21 \\ &{S}_{4}=3+7+11+15=36\end{align}[/latex]

tip for success

We've been introduced to new notation several times in this course. Summation notation is a little bit more complicated than other notations we've seen before (arrow notation, interval notation, etc.). Don't be discouraged if it looks intimidating at first. The parts each stand for something specific so you will become familiar with it through practice and repetition. Try writing out form given in the example below a few times to start. Then, keep your notes nearby as you work through the examples. In time, you won't need your notes to complete problems.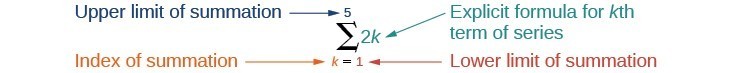
Summation notation is used to represent series. Summation notation is often known as sigma notation because it uses the Greek capital letter sigma, [latex]\Sigma[/latex], to represent the sum. Summation notation includes an explicit formula and specifies the first and last terms in the series. An explicit formula for each term of the series is given to the right of the sigma. A variable called the index of summation is written below the sigma. The index of summation is set equal to the lower limit of summation, which is the number used to generate the first term in the series. The number above the sigma, called the upper limit of summation, is the number used to generate the last term in a series. Explanation of summation notion as described in the text. If we interpret the given notation, we see that it asks us to find the sum of the terms in the series [latex]{a}_{k}=2k[/latex] for [latex]k=1[/latex] through [latex]k=5[/latex]. We can begin by substituting the terms for [latex]k[/latex] and listing out the terms of this series.

[latex]\begin{align} &{a}_{1}=2\left(1\right)=2 \\ &{a}_{2}=2\left(2\right)=4 \\ &{a}_{3}=2\left(3\right)=6 \\ &{a}_{4}=2\left(4\right)=8 \\ &{a}_{5}=2\left(5\right)=10 \end{align}[/latex]

We can find the sum of the series by adding the terms:

[latex]\sum\limits _{k=1}^{5}2k=2+4+6+8+10=30[/latex]

A General Note: Summation Notation

The sum of the first [latex]n[/latex] terms of a series can be expressed in summation notation as follows:

[latex]\sum\limits _{k=1}^{n}{a}_{k}[/latex]

This notation tells us to find the sum of [latex]{a}_{k}[/latex] from

[latex]k=1[/latex] to [latex]k=n[/latex].

[latex]k[/latex] is called the index of summation, 1 is the lower limit of summation, and [latex]n[/latex] is the upper limit of summation.

Q & A

Does the lower limit of summation have to be 1?

No. The lower limit of summation can be any number, but 1 is frequently used. We will look at examples with lower limits of summation other than 1.

How To: Given summation notation for a series, evaluate the value.

  1. Identify the lower limit of summation.
  2. Identify the upper limit of summation.
  3. Substitute each value of [latex]k[/latex] from the lower limit to the upper limit into the formula.
  4. Add to find the sum.

Example: Using Summation Notation

Evaluate [latex]\sum\limits _{k=3}^{7}{k}^{2}[/latex].

Answer: According to the notation, the lower limit of summation is 3 and the upper limit is 7. So we need to find the sum of [latex]{k}^{2}[/latex] from [latex]k=3[/latex] to [latex]k=7[/latex]. We find the terms of the series by substituting [latex]k=3\text{,}4\text{,}5\text{,}6[/latex], and [latex]7[/latex] into the function [latex]{k}^{2}[/latex]. We add the terms to find the sum.

[latex]\begin{align}\sum _{k=3}^{7}{k}^{2} & ={3}^{2}+{4}^{2}+{5}^{2}+{6}^{2}+{7}^{2} \\ & =9+16+25+36+49 \\ \\ & =135 \end{align}[/latex]

Try It

Evaluate [latex]\sum\limits _{k=2}^{5}\left(3k - 1\right)[/latex].

Answer: 38

[embed]

Arithmetic Series

Just as we studied special types of sequences, we will look at special types of series. Recall that an arithmetic sequence is a sequence in which the difference between any two consecutive terms is the common difference, [latex]d[/latex]. The sum of the terms of an arithmetic sequence is called an arithmetic series. We can write the sum of the first [latex]n[/latex] terms of an arithmetic series as:

[latex]{S}_{n}={a}_{1}+\left({a}_{1}+d\right)+\left({a}_{1}+2d\right)+...+\left({a}_{n}-d\right)+{a}_{n}[/latex].

We can also reverse the order of the terms and write the sum as

[latex]{S}_{n}={a}_{n}+\left({a}_{n}-d\right)+\left({a}_{n}-2d\right)+...+\left({a}_{1}+d\right)+{a}_{1}[/latex].

If we add these two expressions for the sum of the first [latex]n[/latex] terms of an arithmetic series, we can derive a formula for the sum of the first [latex]n[/latex] terms of any arithmetic series.

[latex]\begin{align}{S}_{n}&={a}_{1}+\left({a}_{1}+d\right)+\left({a}_{1}+2d\right)+...+\left({a}_{n}-d\right)+{a}_{n} \\ +{S}_{n}&={a}_{n}+\left({a}_{n}-d\right)+\left({a}_{n}-2d\right)+...+\left({a}_{1}+d\right)+{a}_{1} \\ \hline 2{S}_{n}&=\left({a}_{1}+{a}_{n}\right)+\left({a}_{1}+{a}_{n}\right)+...+\left({a}_{1}+{a}_{n}\right) \end{align}[/latex]

Because there are [latex]n[/latex] terms in the series, we can simplify this sum to

[latex]2{S}_{n}=n\left({a}_{1}+{a}_{n}\right)[/latex].

We divide by 2 to find the formula for the sum of the first [latex]n[/latex] terms of an arithmetic series.

[latex]{S}_{n}=\dfrac{n\left({a}_{1}+{a}_{n}\right)}{2}[/latex]

This is generally referred to as the Partial Sum of the series.

tip for success

The formula for finding the partial sum of an arithmetic sequence is handy and should be memorized, but it is important to understand how it was derived.

A General Note: Formula for the Partial Sum of an Arithmetic Series

An arithmetic series is the sum of the terms of an arithmetic sequence. The formula for the partial sum of an arithmetic sequence is

[latex]{S}_{n}=\dfrac{n\left({a}_{1}+{a}_{n}\right)}{2}[/latex]

How To: Given terms of an arithmetic series, find the partial sum

  1. Identify [latex]{a}_{1}[/latex] and [latex]{a}_{n}[/latex].
  2. Determine [latex]n[/latex].
  3. Substitute values for [latex]{a}_{1},{a}_{n}[/latex], and [latex]n[/latex] into the formula [latex]{S}_{n}=\dfrac{n\left({a}_{1}+{a}_{n}\right)}{2}[/latex].
  4. Simplify to find [latex]{S}_{n}[/latex].

tip for success

The examples and problems below may require more than one step to reach the correct conclusion. Some may seem as though they don't give enough information. But you have all the tools your need to solve them in this and in previous sections of this module. Try working them out for yourself on paper before looking at the answers, then analyze your work by comparing to the solutions.

Example: Finding the partial sum of an Arithmetic Series

Find the partial sum of each arithmetic series.
  1. [latex]5 + 8 + 11 + 14 + 17 + 20 + 23 + 26 + 29 + 32[/latex]
  2. [latex]20 + 15 + 10 + \dots + -50[/latex]
  3. [latex]\sum\limits _{k=1}^{12}3k - 8[/latex]

Answer:

  1. We are given [latex]{a}_{1}=5[/latex] and [latex]{a}_{n}=32[/latex].Count the number of terms in the sequence to find [latex]n=10[/latex].Substitute values for [latex]{a}_{1},{a}_{n},[/latex] and [latex]n[/latex] into the formula and simplify. [latex]\begin{align} \\ &{S}_{n}=\dfrac{n\left({a}_{1}+{a}_{n}\right)}{2} \\ &{S}_{10}=\dfrac{10\left(5+32\right)}{2}=185 \\ \text{ }\end{align}[/latex]
  2. We are given [latex]{a}_{1}=20[/latex] and [latex]{a}_{n}=-50[/latex].Use the formula for the general term of an arithmetic sequence to find [latex]n[/latex]. [latex-display]\begin{align}\\ {a}_{n}&={a}_{1}+\left(n - 1\right)d \\ -50&=20+\left(n - 1\right)\left(-5\right) \\ -70&=\left(n - 1\right)\left(-5\right) \\ 14&=n - 1 \\ 15&=n \\ \text{ }\end{align}[/latex-display] Substitute values for [latex]{a}_{1},{a}_{n}\text{,}n[/latex] into the formula and simplify. [latex]\begin{align}\\ &{S}_{n}=\dfrac{n\left({a}_{1}+{a}_{n}\right)}{2} \\ &{S}_{15}=\dfrac{15\left(20 - 50\right)}{2}=-225 \\ \text{ }\end{align}[/latex]
  3. To find [latex]{a}_{1}[/latex], substitute [latex]k=1[/latex] into the given explicit formula. [latex-display]\begin{align}\\ {a}_{k}&=3k - 8 \\ {a}_{1}&=3\left(1\right)-8=-5 \\ \text{ }\end{align}[/latex-display] We are given that [latex]n=12[/latex]. To find [latex]{a}_{12}[/latex], substitute [latex]k=12[/latex] into the given explicit formula. [latex-display]\begin{align} \\{a}_{k}&=3k - 8 \\ {a}_{12}&=3\left(12\right)-8=28 \\ \text{ }\end{align}[/latex-display] Substitute values for [latex]{a}_{1},{a}_{n}[/latex], and [latex]n[/latex] into the formula and simplify. [latex]\begin{align}\\{S}_{n}&=\dfrac{n\left({a}_{1}+{a}_{n}\right)}{2} \\ {S}_{12}&=\dfrac{12\left(-5+28\right)}{2}=138 \end{align}[/latex]

Try It

Use the formula to find the partial sum of each arithmetic series. a.   [latex]1.4+1.6+1.8+2.0+2.2+2.4+2.6+2.8+3.0+3.2+3.4[/latex]

Answer: [latex]26.4[/latex]

b.   [latex]12+21+29\dots + 69[/latex]

Answer: [latex-display]328[/latex-display]

c.   [latex]\sum\limits _{k=1}^{10}5 - 6k[/latex]

Answer: [latex-display]-280[/latex-display]

[embed] [embed]

Example: Solving Application Problems with Arithmetic Series

On the Sunday after a minor surgery, a woman is able to walk a half-mile. Each Sunday, she walks an additional quarter-mile. After 8 weeks, what will be the total number of miles she has walked?

Answer: This problem can be modeled by an arithmetic series with [latex]{a}_{1}=\frac{1}{2}[/latex] and [latex]d=\frac{1}{4}[/latex]. We are looking for the total number of miles walked after 8 weeks, so we know that [latex]n=8[/latex], and we are looking for [latex]{S}_{8}[/latex]. To find [latex]{a}_{8}[/latex], we can use the explicit formula for an arithmetic sequence.

[latex]\begin{align} {a}_{n}&={a}_{1}+d\left(n - 1\right) \\ {a}_{8}&=\dfrac{1}{2}+\dfrac{1}{4}\left(8 - 1\right)=\dfrac{9}{4} \end{align}[/latex]

We can now use the formula for arithmetic series.

[latex]\begin{align} {S}_{n}&=\dfrac{n\left({a}_{1}+{a}_{n}\right)}{2} \\ {S}_{8}&=\dfrac{8\left(\frac{1}{2}+\frac{9}{4}\right)}{2}=11 \end{align}[/latex]

She will have walked a total of 11 miles.

Try It

A man earns $100 in the first week of June. Each week, he earns $12.50 more than the previous week. After 12 weeks, how much has he earned?

Answer: $2,025

[embed]
 

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 5865, 5867. Authored by: WebWork-Rochester. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY +GPL.
  • Question ID 128790,128791. Authored by: Day, Alyson. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.