We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Equations of Lines

Now that we've learned how to plot points on a coordinate plane and graph linear equations, we can begin to analyze the equations of lines and evaluate the different characteristics of these lines. In this section, we'll learn about the commonly used forms for writing linear equations and the properties of lines that can be determined from their equations. For example, without creating a table of values, you will be able to match each equation below to its corresponding graph. You will also be able to explain the similarities and differences of each line, how they relate to each other, and why they behave that way.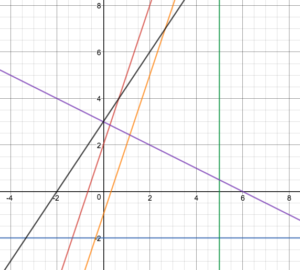   6 lines graphed on a coordinate plane. (a) [latex]y=3x+2[/latex] (b) [latex]y-4=-\frac{1}{2}(x+2)[/latex] (c) [latex]x=5[/latex] (d) [latex]y=-2[/latex] (e) [latex]3x=y+1[/latex] (f) [latex]2y-3x=6[/latex]        

Writing Equations of Lines

Slope-Intercept Form

Perhaps the most familiar form of a linear equation is the slope-intercept form, written as [latex]y=mx+b[/latex], where [latex]m=\text{slope}[/latex] and [latex]b=y\text{-intercept}[/latex]. Let us begin with the slope.

The Slope of a Line

The slope of a line refers to the ratio of the vertical change in y over the horizontal change in x between any two points on a line. It indicates the direction in which a line slants as well as its steepness. Slope is sometimes described as rise over run.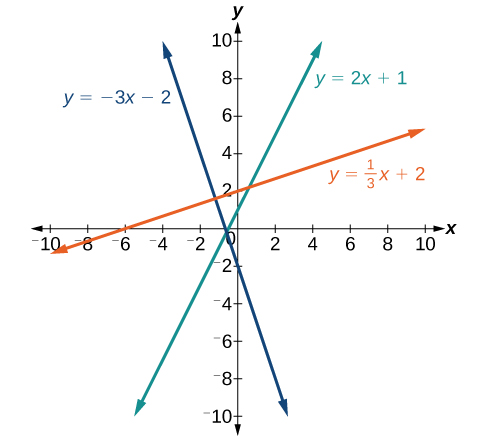
[latex]m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]
If the slope is positive, the line slants to the right. If the slope is negative, the line slants to the left. As the slope increases, the line becomes steeper. Some examples are shown below. The lines indicate the following slopes: [latex]m=-3[/latex], [latex]m=2[/latex], and [latex]m=\frac{1}{3}[/latex]. Coordinate plane with the x and y axes ranging from negative 10 to 10. Three linear functions are plotted: y = negative 3 times x minus 2; y = 2 times x plus 1; and y = x over 3 plus 2.

A General Note: The Slope of a Line

The slope of a line, m, represents the change in y over the change in x. Given two points, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the following formula determines the slope of a line containing these points:
[latex]m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]

Example: Finding the Slope of a Line Given Two Points

Find the slope of a line that passes through the points [latex]\left(2,-1\right)[/latex] and [latex]\left(-5,3\right)[/latex].

Answer: We substitute the y-values and the x-values into the formula.

[latex]\begin{array}{l}m\hfill&=\frac{3-\left(-1\right)}{-5 - 2}\hfill \\ \hfill&=\frac{4}{-7}\hfill \\ \hfill&=-\frac{4}{7}\hfill \end{array}[/latex]
The slope is [latex]-\frac{4}{7}[/latex].

Analysis of the Solution

It does not matter which point is called [latex]\left({x}_{1},{y}_{1}\right)[/latex] or [latex]\left({x}_{2},{y}_{2}\right)[/latex]. As long as we are consistent with the order of the y terms and the order of the x terms in the numerator and denominator, the calculation will yield the same result.

Try It

Find the slope of the line that passes through the points [latex]\left(-2,6\right)[/latex] and [latex]\left(1,4\right)[/latex].

Answer: [latex]m = - \frac{2}{3}[/latex]

Example: Finding the Equation of a Line Passing Through Two Given Points

Find the equation of the line passing through the points [latex]\left(3,4\right)[/latex] and [latex]\left(0,-3\right)[/latex]. Write the final equation in slope-intercept form.

Answer: First, we calculate the slope using the slope formula and two points.

[latex]\begin{array}{l}\hfill \\ m=\frac{-3 - 4}{0 - 3}\hfill \\ =\frac{-7}{-3}\hfill \\ =\frac{7}{3}\hfill \end{array}[/latex]
Next, we use the point-slope formula with the slope of [latex]\frac{7}{3}[/latex], and either point. Let’s pick the point [latex]\left(3,4\right)[/latex] for [latex]\left({x}_{1},{y}_{1}\right)[/latex].
[latex]\begin{array}{l}y - 4=\frac{7}{3}\left(x - 3\right)\hfill \\ y - 4=\frac{7}{3}x - 7\hfill&\text{Distribute the }\frac{7}{3}.\hfill \\ y=\frac{7}{3}x - 3\hfill \end{array}[/latex]
In slope-intercept form, the equation is written as [latex]y=\frac{7}{3}x - 3[/latex].

Analysis of the Solution

To prove that either point can be used, let us use the second point [latex]\left(0,-3\right)[/latex] and see if we get the same equation.
[latex]\begin{array}{l}y-\left(-3\right)=\frac{7}{3}\left(x - 0\right)\hfill \\ y+3=\frac{7}{3}x\hfill \\ y=\frac{7}{3}x - 3\hfill \end{array}[/latex]
We see that the same line will be obtained using either point. This makes sense because we used both points to calculate the slope.

Standard Form of a Line

Another way that we can represent the equation of a line is in standard form. Standard form is given as
[latex]Ax+By=C[/latex]
where [latex]A[/latex], [latex]B[/latex], and [latex]C[/latex] are integers. The x- and y-terms are on one side of the equal sign and the constant term is on the other side.

Example: Finding the Equation of a Line and Writing It in Standard Form

Find the equation of the line with [latex]m=-6[/latex] and passing through the point [latex]\left(\frac{1}{4},-2\right)[/latex]. Write the equation in standard form.

Answer: We begin using the point-slope formula.

[latex]\begin{array}{l}y-\left(-2\right)=-6\left(x-\frac{1}{4}\right)\hfill \\ y+2=-6x+\frac{3}{2}\hfill \end{array}[/latex]
From here, we multiply through by 2, as no fractions are permitted in standard form, and then move both variables to the left aside of the equal sign and move the constants to the right.
[latex]\begin{array}{l}2\left(y+2\right)=\left(-6x+\frac{3}{2}\right)2\hfill \\ 2y+4=-12x+3\hfill \\ 12x+2y=-1\hfill \end{array}[/latex]
This equation is now written in standard form.

Try It

Find the equation of the line in standard form with slope [latex]m=-\frac{1}{3}[/latex] and passing through the point [latex]\left(1,\frac{1}{3}\right)[/latex].

Answer: [latex]x+3y=2[/latex]

If we know the equation of a line, we can use what we know about slope to write the equation of a line that is either parallel or perpendicular to the given line.

Writing Equations of Parallel Lines

Suppose for example, we are given the following equation.

[latex]f\left(x\right)=3x+1[/latex]

We know that the slope of the line formed by the function is 3. We also know that the y-intercept is (0, 1). Any other line with a slope of 3 will be parallel to f(x). So the lines formed by all of the following functions will be parallel to f(x).

[latex]\begin{cases}g\left(x\right)=3x+6\hfill \\ h\left(x\right)=3x+1\hfill \\ p\left(x\right)=3x+\frac{2}{3}\hfill \end{cases}[/latex]

Suppose then we want to write the equation of a line that is parallel to f and passes through the point (1, 7). We already know that the slope is 3. We just need to determine which value for b will give the correct line. We can begin with the point-slope form of an equation for a line, and then rewrite it in the slope-intercept form.

[latex]\begin{cases}y-{y}_{1}=m\left(x-{x}_{1}\right)\hfill \\ y - 7=3\left(x - 1\right)\hfill \\ y - 7=3x - 3\hfill \\ \text{ }y=3x+4\hfill \end{cases}[/latex]

So [latex]g\left(x\right)=3x+4[/latex] is parallel to [latex]f\left(x\right)=3x+1[/latex] and passes through the point (1, 7).

How To: Given the equation of a function and a point through which its graph passes, write the equation of a line parallel to the given line that passes through the given point.

  1. Find the slope of the function.
  2. Substitute the given values into either the general point-slope equation or the slope-intercept equation for a line.
  3. Simplify.

Example: Finding a Line Parallel to a Given Line

Find a line parallel to the graph of [latex]f\left(x\right)=3x+6[/latex] that passes through the point (3, 0).

Answer: The slope of the given line is 3. If we choose the slope-intercept form, we can substitute m = 3, x = 3, and f(x) = 0 into the slope-intercept form to find the y-intercept.

[latex]\begin{cases}g\left(x\right)=3x+b\hfill \\ \text{ }0=3\left(3\right)+b\hfill \\ \text{ }b=-9\hfill \end{cases}[/latex]

The line parallel to f(x) that passes through (3, 0) is [latex]g\left(x\right)=3x - 9[/latex].

Analysis of the Solution

We can confirm that the two lines are parallel by graphing them. The graph below shows that the two lines will never intersect.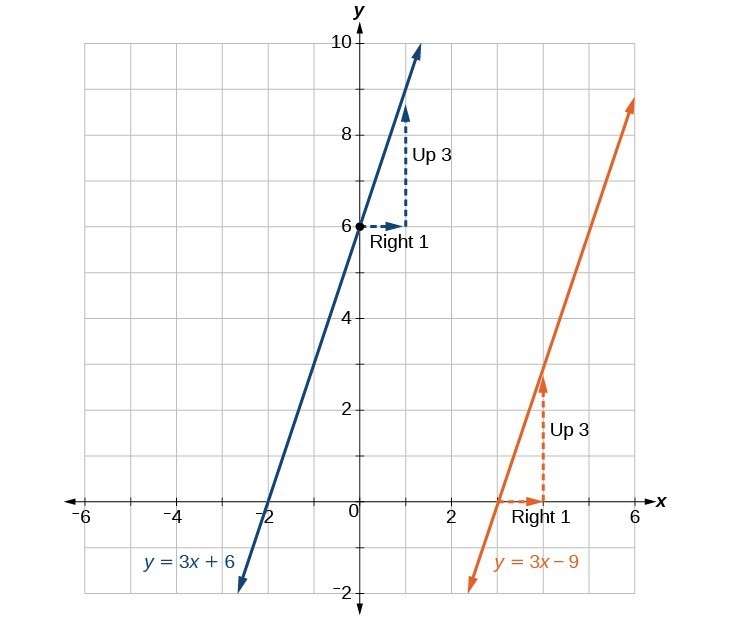 Graph of two functions where the blue line is y = 3x + 6, and the orange line is y = 3x - 9.

   

Writing Equations of Perpendicular Lines

We can use a very similar process to write the equation for a line perpendicular to a given line. Instead of using the same slope, however, we use the negative reciprocal of the given slope. Suppose we are given the following function:

[latex]f\left(x\right)=2x+4[/latex]

The slope of the line is 2, and its negative reciprocal is [latex]-\frac{1}{2}[/latex]. Any function with a slope of [latex]-\frac{1}{2}[/latex] will be perpendicular to f(x). So the lines formed by all of the following functions will be perpendicular to f(x).

[latex]\begin{cases}g\left(x\right)=-\frac{1}{2}x+4\hfill \\ h\left(x\right)=-\frac{1}{2}x+2\hfill \\ p\left(x\right)=-\frac{1}{2}x-\frac{1}{2}\hfill \end{cases}[/latex]

As before, we can narrow down our choices for a particular perpendicular line if we know that it passes through a given point. Suppose then we want to write the equation of a line that is perpendicular to f(x) and passes through the point (4, 0). We already know that the slope is [latex]-\frac{1}{2}[/latex]. Now we can use the point to find the y-intercept by substituting the given values into the slope-intercept form of a line and solving for b.

[latex]\begin{cases}g\left(x\right)=mx+b\hfill \\ 0=-\frac{1}{2}\left(4\right)+b\hfill \\ 0=-2+b\hfill \\ 2=b\hfill \\ b=2\hfill \end{cases}[/latex]

The equation for the function with a slope of [latex]-\frac{1}{2}[/latex] and a y-intercept of 2 is [latex]g\left(x\right)=-\frac{1}{2}x+2[/latex]. So [latex]g\left(x\right)=-\frac{1}{2}x+2[/latex] is perpendicular to [latex]f\left(x\right)=2x+4[/latex] and passes through the point (4, 0). Be aware that perpendicular lines may not look obviously perpendicular on a graphing calculator unless we use the square zoom feature.

Q & A

A horizontal line has a slope of zero and a vertical line has an undefined slope. These two lines are perpendicular, but the product of their slopes is not –1. Doesn’t this fact contradict the definition of perpendicular lines? No. For two perpendicular linear functions, the product of their slopes is –1. However, a vertical line is not a function so the definition is not contradicted.

How To: Given the equation of a function and a point through which its graph passes, write the equation of a line perpendicular to the given line.

  1. Find the slope of the function.
  2. Determine the negative reciprocal of the slope.
  3. Substitute the new slope and the values for x and y from the coordinate pair provided into [latex]g\left(x\right)=mx+b[/latex].
  4. Solve for b.
  5. Write the equation for the line.

Example: Finding the Equation of a Perpendicular Line

Find the equation of a line perpendicular to [latex]y=3x+3[/latex] that passes through the point (3, 0).

Answer: The original line has slope m = 3, so the slope of the perpendicular line will be its negative reciprocal, or [latex]-\frac{1}{3}[/latex]. Using this slope and the given point, we can find the equation for the line.

[latex]\begin{cases}y_{2}=-\frac{1}{3}x+b\hfill \\ \text{ }0=-\frac{1}{3}\left(3\right)+b\hfill \\ \text{ }1=b\hfill \\ \text{ }b=1\hfill \end{cases}[/latex]

The line perpendicular to y that passes through (3, 0) is [latex]y_{2}=-\frac{1}{3}x+1[/latex].

Analysis of the Solution

A graph of the two lines is shown in the graph below.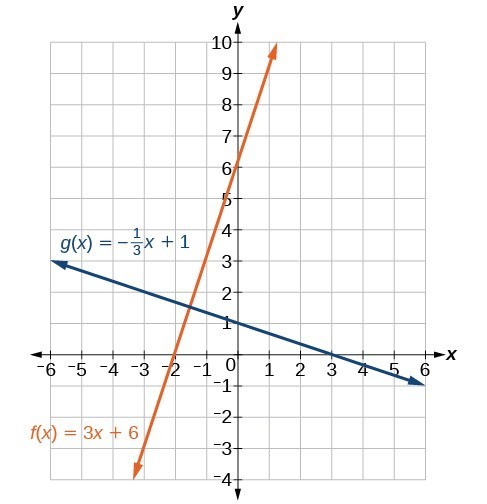 Graph of two functions where the blue line is g(x) = -1/3x + 1, and the orange line is f(x) = 3x + 6.

Try It

Given the line [latex]y=2x - 4[/latex], write an equation for the line passing through (0, 0) that is
  1. parallel to y
  2. perpendicular to y

Answer:

  1. [latex]y=2x[/latex]is parallel
  2. [latex]y=-\frac{1}{2}x[/latex]is perpendicular

Example: Finding the Equation of a Line Perpendicular to a Given Line Passing Through a Given Point

Find the equation of the line perpendicular to [latex]5x - 3y+4=0\left(-4,1\right)[/latex].

Answer: The first step is to write the equation in slope-intercept form.

[latex]\begin{array}{l}5x - 3y+4=0\hfill \\ -3y=-5x - 4\hfill \\ y=\frac{5}{3}x+\frac{4}{3}\hfill \end{array}[/latex]

We see that the slope is [latex]m=\frac{5}{3}[/latex]. This means that the slope of the line perpendicular to the given line is the negative reciprocal, or [latex]-\frac{3}{5}[/latex]. Next, we use the point-slope formula with this new slope and the given point.

[latex]\begin{array}{l}y - 1=-\frac{3}{5}\left(x-\left(-4\right)\right)\hfill \\ y - 1=-\frac{3}{5}x-\frac{12}{5}\hfill \\ y=-\frac{3}{5}x-\frac{12}{5}+\frac{5}{5}\hfill \\ y=-\frac{3}{5}x-\frac{7}{5}\hfill \end{array}[/latex]

Key Concepts

  • Given two points, we can find the slope of a line using the slope formula.
  • We can identify the slope and y-intercept of an equation in slope-intercept form.
  • We can find the equation of a line given the slope and a point.
  • We can also find the equation of a line given two points. Find the slope and use the point-slope formula.
  • The standard form of a line has no fractions.
  • Horizontal lines have a slope of zero and are defined as [latex]y=c[/latex], where c is a constant.
  • Vertical lines have an undefined slope (zero in the denominator), and are defined as [latex]x=c[/latex], where c is a constant.
  • Parallel lines have the same slope and different y-intercepts.
  • Perpendicular lines have slopes that are negative reciprocals of each other unless one is horizontal and the other is vertical.
  • A linear equation can be used to solve for an unknown in a number problem.

Glossary

slope the change in y-values over the change in x-values      

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 1719. Authored by: Barbara Goldner. License: CC BY: Attribution. License terms: IMathAS Community License CC- BY + GPL.
  • Question ID 110942, 110946, 110951, 110952, 110960, 110970, 110971. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 1436. Authored by: WebWork-Rochester. License: CC BY: Attribution. License terms: IMathAS Community License CC- BY + GPL.

CC licensed content, Specific attribution

  • College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. License: CC BY: Attribution.