Characteristics of Functions and Their Graphs
A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.
Characteristics of Functions
A relation is a set of ordered pairs. The set of the first components of each ordered pair is called the domain and the set of the second components of each ordered pair is called the range. Consider the following set of ordered pairs. The first numbers in each pair are the first five natural numbers. The second number in each pair is twice that of the first.[latex]\left\{\left(1,2\right),\left(2,4\right),\left(3,6\right),\left(4,8\right),\left(5,10\right)\right\}[/latex]
The domain is [latex]\left\{1,2,3,4,5\right\}[/latex]. The range is [latex]\left\{2,4,6,8,10\right\}[/latex]. Note that each value in the domain is also known as an input value, or independent variable, and is often labeled with the lowercase letter [latex]x[/latex]. Each value in the range is also known as an output value, or dependent variable, and is often labeled lowercase letter [latex]y[/latex]. A function [latex]f[/latex] is a relation that assigns a single value in the range to each value in the domain. In other words, no x-values are repeated. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, [latex]\left\{1,2,3,4,5\right\}[/latex], is paired with exactly one element in the range, [latex]\left\{2,4,6,8,10\right\}[/latex]. Now let’s consider the set of ordered pairs that relates the terms "even" and "odd" to the first five natural numbers. It would appear as[latex]\left\{\left(\text{odd},1\right),\left(\text{even},2\right),\left(\text{odd},3\right),\left(\text{even},4\right),\left(\text{odd},5\right)\right\}[/latex]
Notice that each element in the domain, [latex]\left\{\text{even,}\text{odd}\right\}[/latex] is not paired with exactly one element in the range, [latex]\left\{1,2,3,4,5\right\}[/latex]. For example, the term "odd" corresponds to three values from the domain, [latex]\left\{1,3,5\right\}[/latex] and the term "even" corresponds to two values from the range, [latex]\left\{2,4\right\}[/latex]. This violates the definition of a function, so this relation is not a function. This image compares relations that are functions and not functions.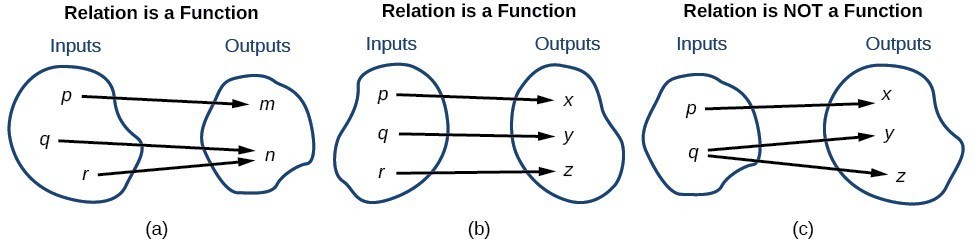 (a) This relationship is a function because each input is associated with a single output. Note that input [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. (b) This relationship is also a function. In this case, each input is associated with a single output. (c) This relationship is not a function because input [latex]q[/latex] is associated with two different outputs.
(a) This relationship is a function because each input is associated with a single output. Note that input [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. (b) This relationship is also a function. In this case, each input is associated with a single output. (c) This relationship is not a function because input [latex]q[/latex] is associated with two different outputs.A General Note: Function
A function is a relation in which each possible input value leads to exactly one output value. We say "the output is a function of the input." The input values make up the domain, and the output values make up the range.How To: Given a relationship between two quantities, determine whether the relationship is a function.
- Identify the input values.
- Identify the output values.
- If each input value leads to only one output value, classify the relationship as a function. If any input value leads to two or more outputs, do not classify the relationship as a function.
Example: Determining If Menu Price Lists Are Functions
The coffee shop menu consists of items and their prices.- Is price a function of the item?
- Is the item a function of the price?

Answer:
- Let’s begin by considering the input as the items on the menu. The output values are then the prices.
 Each item on the menu has only one price, so the price is a function of the item.
Each item on the menu has only one price, so the price is a function of the item. - Two items on the menu have the same price. If we consider the prices to be the input values and the items to be the output, then the same input value could have more than one output associated with it.
 Therefore, the item is a not a function of price.
Therefore, the item is a not a function of price.
Example: Determining If Class Grade Rules Are Functions
In a particular math class, the overall percent grade corresponds to a grade point average. Is grade point average a function of the percent grade? Is the percent grade a function of the grade point average? The table below shows a possible rule for assigning grade points.| Percent Grade | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
|---|---|---|---|---|---|---|---|---|
| Grade Point Average | 0.0 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Answer: For any percent grade earned, there is an associated grade point average, so the grade point average is a function of the percent grade. In other words, if we input the percent grade, the output is a specific grade point average. In the grading system given, there is a range of percent grades that correspond to the same grade point average. For example, students who receive a grade point average of 3.0 could have a variety of percent grades ranging from 78 all the way to 86. Thus, percent grade is not a function of grade point average.
Try It
The table below lists the five greatest baseball players of all time in order of rank.| Player | Rank |
|---|---|
| Babe Ruth | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Aaron | 5 |
- Is the rank a function of the player name?
- Is the player name a function of the rank?
Answer:
- yes
- yes. (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)
Q & A
Instead of a notation such as [latex]y=f\left(x\right)[/latex], could we use the same symbol for the output as for the function, such as [latex]y=y\left(x\right)[/latex], meaning "y is a function of x?" Yes, this is often done, especially in applied subjects that use higher math, such as physics and engineering. However, in exploring math itself we like to maintain a distinction between a function such as [latex]f[/latex], which is a rule or procedure, and the output [latex]y[/latex] we get by applying [latex]f[/latex] to a particular input [latex]x[/latex]. This is why we usually use notation such as [latex]y=f\left(x\right),P=W\left(d\right)[/latex], and so on.Representing Functions Using Tables
A common method of representing functions is in the form of a table. The table rows or columns display the corresponding input and output values. In some cases, these values represent all we know about the relationship; other times, the table provides a few select examples from a more complete relationship. The table below lists the input number of each month (January = 1, February = 2, and so on) and the output value of the number of days in that month. This information represents all we know about the months and days for a given year (that is not a leap year). Note that, in this table, we define a days-in-a-month function [latex]f[/latex] where [latex]D=f\left(m\right)[/latex] identifies months by an integer rather than by name.| Month number, [latex]m[/latex] (input) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Days in month, [latex]D[/latex] (output) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
| [latex]n[/latex] | 1 | 2 | 3 | 4 | 5 |
| [latex]Q[/latex] | 8 | 6 | 7 | 6 | 8 |
| Age in years, [latex]\text{ }a\text{ }[/latex] (input) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Height in inches, [latex]\text{ }h\text{ }[/latex] (output) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
How To: Given a table of input and output values, determine whether the table represents a function.
- Identify the input and output values.
- Check to see if each input value is paired with only one output value. If so, the table represents a function.
Example: Identifying Tables that Represent Functions
Which table, a), b), or c), represents a function (if any)?| Table A | |
|---|---|
| Input | Output |
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Table B | |
|---|---|
| Input | Output |
| –3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Table C | |
|---|---|
| Input | Output |
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Answer: a) and b) define functions. In both, each input value corresponds to exactly one output value. c) does not define a function because the input value of 5 corresponds to two different output values. When a table represents a function, corresponding input and output values can also be specified using function notation. The function represented by a) can be represented by writing
[latex]f\left(2\right)=1,f\left(5\right)=3,\text{and }f\left(8\right)=6[/latex]
Similarly, the statements [latex]g\left(-3\right)=5,g\left(0\right)=1,\text{and }g\left(4\right)=5[/latex] represent the function in b). c) cannot be expressed in a similar way because it does not represent a function.Evaluate and Solve Functions
When we have a function in formula form, it is usually a simple matter to evaluate the function. For example, the function [latex]f\left(x\right)=5 - 3{x}^{2}[/latex] can be evaluated by squaring the input value, multiplying by 3, and then subtracting the product from 5.How To: Given the formula for a function, evaluate.
- Replace the input variable in the formula with the value provided.
- Calculate the result.
Example: Evaluating Functions
Given the function [latex]h\left(p\right)={p}^{2}+2p[/latex], evaluate [latex]h\left(4\right)[/latex].Answer:
To evaluate [latex]h\left(4\right)[/latex], we substitute the value 4 for the input variable [latex]p[/latex] in the given function. [latex]\begin{cases}\text{ }h\left(p\right)={p}^{2}+2p\hfill \\ \text{ }h\left(4\right)={\left(4\right)}^{2}+2\left(4\right)\hfill \\ \text{ }=16+8\hfill \\ \text{ }=24\hfill \end{cases}[/latex]
Therefore, for an input of 4, we have an output of 24.Example: Evaluating Functions at Specific Values
Evaluate [latex]f\left(x\right)={x}^{2}+3x - 4[/latex] at- [latex]2[/latex]
- [latex]a[/latex]
- [latex]a+h[/latex]
- [latex]\frac{f\left(a+h\right)-f\left(a\right)}{h}[/latex]
Answer: Replace the [latex]x[/latex] in the function with each specified value.
- Because the input value is a number, 2, we can use algebra to simplify.
[latex]\begin{cases}f\left(2\right)={2}^{2}+3\left(2\right)-4\hfill \\ =4+6 - 4\hfill \\ =6\hfill \end{cases}[/latex]
- In this case, the input value is a letter so we cannot simplify the answer any further.
[latex]f\left(a\right)={a}^{2}+3a - 4[/latex]
- With an input value of [latex]a+h[/latex], we must use the distributive property.
[latex]\begin{cases}f\left(a+h\right)={\left(a+h\right)}^{2}+3\left(a+h\right)-4\hfill \\ ={a}^{2}+2ah+{h}^{2}+3a+3h - 4\hfill \end{cases}[/latex]
- In this case, we apply the input values to the function more than once, and then perform algebraic operations on the result. We already found that
[latex]f\left(a+h\right)={a}^{2}+2ah+{h}^{2}+3a+3h - 4[/latex]and we know that[latex]f\left(a\right)={a}^{2}+3a - 4[/latex]Now we combine the results and simplify.
[latex]\begin{cases}\begin{cases}\hfill \\ \frac{f\left(a+h\right)-f\left(a\right)}{h}=\frac{\left({a}^{2}+2ah+{h}^{2}+3a+3h - 4\right)-\left({a}^{2}+3a - 4\right)}{h}\hfill \end{cases}\hfill \\ \begin{cases}\text{ }=\frac{2ah+{h}^{2}+3h}{h}\hfill & \hfill \\ \text{ }=\frac{h\left(2a+h+3\right)}{h}\hfill & \begin{cases}{cc}\begin{cases}{cc}& \end{cases}& \end{cases}\text{Factor out }h.\hfill \\ \text{ }=2a+h+3\hfill & \begin{cases}{cc}\begin{cases}{cc}& \end{cases}& \end{cases}\text{Simplify}.\hfill \end{cases}\hfill \end{cases}[/latex]
Example: Solving Functions
Given the function [latex]h\left(p\right)={p}^{2}+2p[/latex], solve for [latex]h\left(p\right)=3[/latex].Answer:
[latex]\begin{cases}\text{ }h\left(p\right)=3\hfill & \hfill & \hfill & \hfill \\ \text{ }{p}^{2}+2p=3\hfill & \hfill & \hfill & \text{Substitute the original function }h\left(p\right)={p}^{2}+2p.\hfill \\ \text{ }{p}^{2}+2p - 3=0\hfill & \hfill & \hfill & \text{Subtract 3 from each side}.\hfill \\ \text{ }\left(p+3\text{)(}p - 1\right)=0\hfill & \hfill & \hfill & \text{Factor}.\hfill \end{cases}[/latex]
If [latex]\left(p+3\right)\left(p - 1\right)=0[/latex], either [latex]\left(p+3\right)=0[/latex] or [latex]\left(p - 1\right)=0[/latex] (or both of them equal 0). We will set each factor equal to 0 and solve for [latex]p[/latex] in each case.[latex]\begin{cases}\left(p+3\right)=0,\hfill & p=-3\hfill \\ \left(p - 1\right)=0,\hfill & p=1\hfill \end{cases}[/latex]
This gives us two solutions. The output [latex]h\left(p\right)=3[/latex] when the input is either [latex]p=1[/latex] or [latex]p=-3[/latex].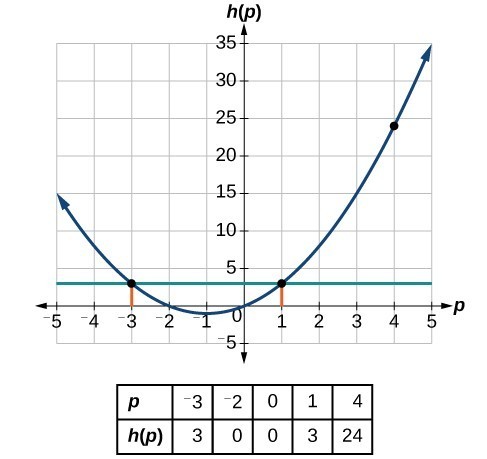 We can also verify by graphing as in Figure 5. The graph verifies that [latex]h\left(1\right)=h\left(-3\right)=3[/latex] and [latex]h\left(4\right)=24[/latex].
We can also verify by graphing as in Figure 5. The graph verifies that [latex]h\left(1\right)=h\left(-3\right)=3[/latex] and [latex]h\left(4\right)=24[/latex].
Try It
Given the function [latex]g\left(m\right)=\sqrt{m - 4}[/latex], solve [latex]g\left(m\right)=2[/latex].Answer: [latex-display]m=8[/latex-display]
Q & A
Are there relationships expressed by an equation that do represent a function but which still cannot be represented by an algebraic formula? Yes, this can happen. For example, given the equation [latex]x=y+{2}^{y}[/latex], if we want to express [latex]y[/latex] as a function of [latex]x[/latex], there is no simple algebraic formula involving only [latex]x[/latex] that equals [latex]y[/latex]. However, each [latex]x[/latex] does determine a unique value for [latex]y[/latex], and there are mathematical procedures by which [latex]y[/latex] can be found to any desired accuracy. In this case, we say that the equation gives an implicit (implied) rule for [latex]y[/latex] as a function of [latex]x[/latex], even though the formula cannot be written explicitly.Evaluating a Function Given in Tabular Form
As we saw above, we can represent functions in tables. Conversely, we can use information in tables to write functions, and we can evaluate functions using the tables. For example, how well do our pets recall the fond memories we share with them? There is an urban legend that a goldfish has a memory of 3 seconds, but this is just a myth. Goldfish can remember up to 3 months, while the beta fish has a memory of up to 5 months. And while a puppy’s memory span is no longer than 30 seconds, the adult dog can remember for 5 minutes. This is meager compared to a cat, whose memory span lasts for 16 hours. The function that relates the type of pet to the duration of its memory span is more easily visualized with the use of a table. See the table below.| Pet | Memory span in hours |
|---|---|
| Puppy | 0.008 |
| Adult dog | 0.083 |
| Cat | 16 |
| Goldfish | 2160 |
| Beta fish | 3600 |
How To: Given a function represented by a table, identify specific output and input values.
- Find the given input in the row (or column) of input values.
- Identify the corresponding output value paired with that input value.
- Find the given output values in the row (or column) of output values, noting every time that output value appears.
- Identify the input value(s) corresponding to the given output value.
Example: Evaluating and Solving a Tabular Function
Using the table below,- Evaluate [latex]g\left(3\right)[/latex].
- Solve [latex]g\left(n\right)=6[/latex].
| n | 1 | 2 | 3 | 4 | 5 |
| g(n) | 8 | 6 | 7 | 6 | 8 |
Answer:
- Evaluating [latex]g\left(3\right)[/latex] means determining the output value of the function [latex]g[/latex] for the input value of [latex]n=3[/latex]. The table output value corresponding to [latex]n=3[/latex] is 7, so [latex]g\left(3\right)=7[/latex].
- Solving [latex]g\left(n\right)=6[/latex] means identifying the input values, [latex]n[/latex], that produce an output value of 6. The table below shows two solutions: [latex]n=2[/latex] and [latex]n=4[/latex].
| n | 1 | 2 | 3 | 4 | 5 |
| g(n) | 8 | 6 | 7 | 6 | 8 |
Try It
Using the table from the previous example, evaluate [latex]g\left(1\right)[/latex] .Answer: [latex]g\left(1\right)=8[/latex]
Using the Horizontal Line Test
Once we have determined that a graph defines a function, an easy way to determine if it is a one-to-one function is to use the horizontal line test. Draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.How To: Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function.
- Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
- If there is any such line, determine that the function is not one-to-one.
Example: Applying the Horizontal Line Test
Consider the functions (a), and (b)shown in the graphs below.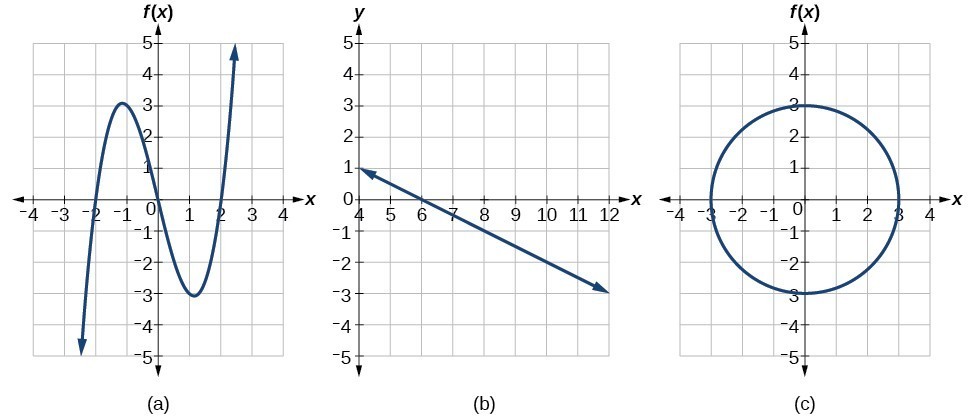 Are either of the functions one-to-one?
Are either of the functions one-to-one?
Answer:
The function in (a) is not one-to-one. The horizontal line shown below intersects the graph of the function at two points (and we can even find horizontal lines that intersect it at three points.)
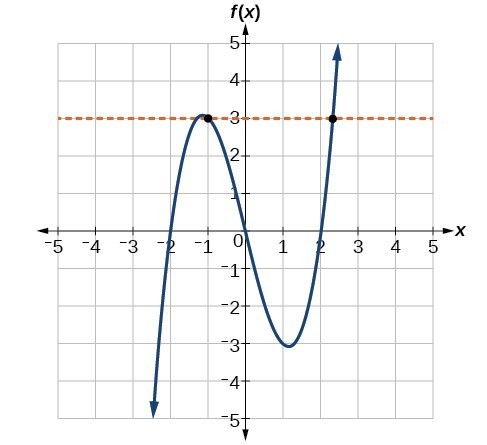 The function in (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once.
The function in (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once.
Identifying Basic Toolkit Functions
In this text, we will be exploring functions—the shapes of their graphs, their unique characteristics, their algebraic formulas, and how to solve problems with them. When learning to read, we start with the alphabet. When learning to do arithmetic, we start with numbers. When working with functions, it is similarly helpful to have a base set of building-block elements. We call these our "toolkit functions," which form a set of basic named functions for which we know the graph, formula, and special properties. Some of these functions are programmed to individual buttons on many calculators. For these definitions we will use [latex]x[/latex] as the input variable and [latex]y=f\left(x\right)[/latex] as the output variable. We will see these toolkit functions, combinations of toolkit functions, their graphs, and their transformations frequently throughout this book. It will be very helpful if we can recognize these toolkit functions and their features quickly by name, formula, graph, and basic table properties. The graphs and sample table values are included with each function shown below.| Toolkit Functions | ||
|---|---|---|
| Name | Function | Graph |
| Constant | [latex]f\left(x\right)=c[/latex], where [latex]c[/latex] is a constant | 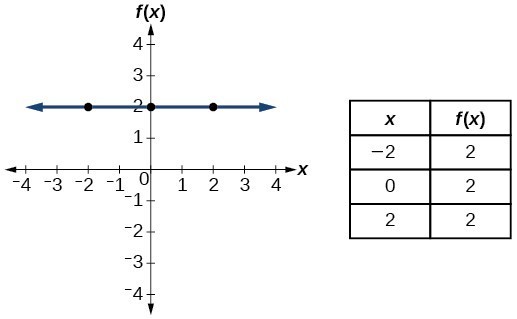 |
| Identity | [latex]f\left(x\right)=x[/latex] |  |
| Absolute value | [latex]f\left(x\right)=|x|[/latex] | 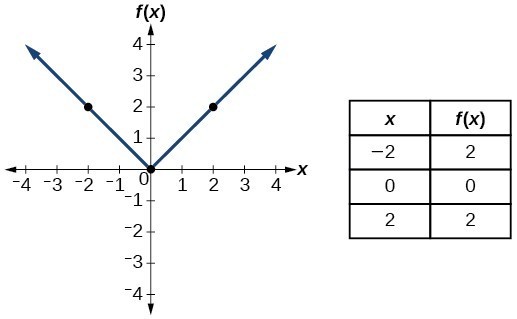 |
| Quadratic | [latex]f\left(x\right)={x}^{2}[/latex] |  |
| Cubic | [latex]f\left(x\right)={x}^{3}[/latex] | 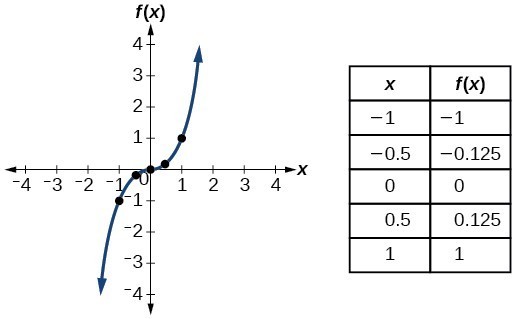 |
| Reciprocal/ Rational | [latex]f\left(x\right)=\frac{1}{x}[/latex] | 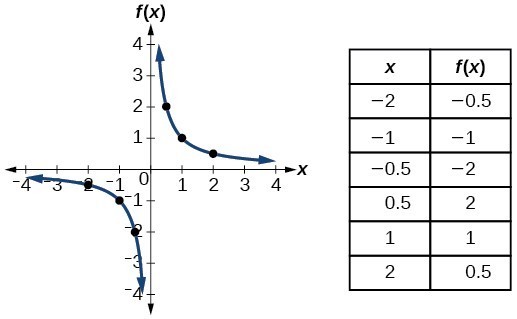 |
| Reciprocal / Rational squared | [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex] | 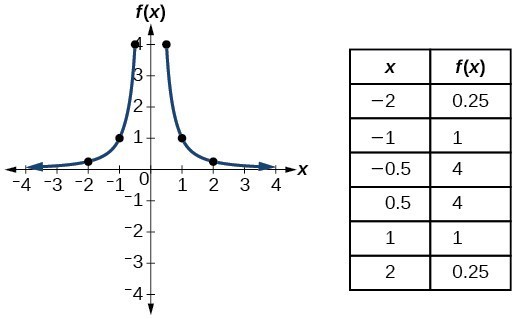 |
| Square root | [latex]f\left(x\right)=\sqrt{x}[/latex] | 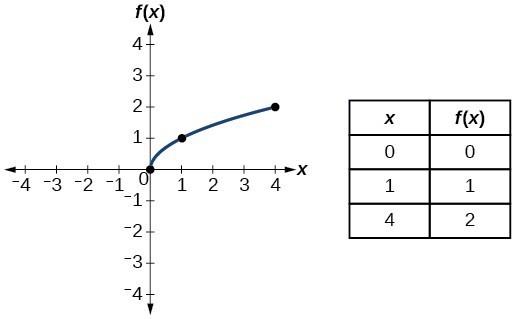 |
| Cube root | [latex]f\left(x\right)=\sqrt[3]{x}[/latex] | 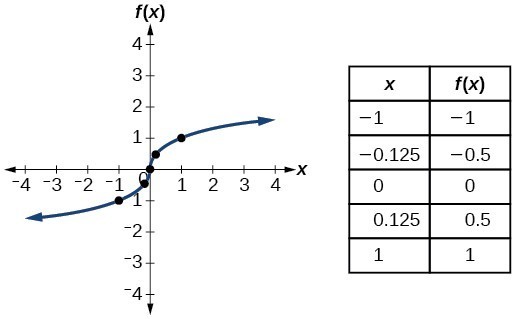 |
Key Equations
| Constant function | [latex]f\left(x\right)=c[/latex], where [latex]c[/latex] is a constant |
| Identity function | [latex]f\left(x\right)=x[/latex] |
| Absolute value function | [latex]f\left(x\right)=|x|[/latex] |
| Quadratic function | [latex]f\left(x\right)={x}^{2}[/latex] |
| Cubic function | [latex]f\left(x\right)={x}^{3}[/latex] |
| Reciprocal function | [latex]f\left(x\right)=\frac{1}{x}[/latex] |
| Reciprocal squared function | [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex] |
| Square root function | [latex]f\left(x\right)=\sqrt{x}[/latex] |
| Cube root function | [latex]f\left(x\right)=\sqrt[3]{x}[/latex] |
Key Concepts
- A relation is a set of ordered pairs. A function is a specific type of relation in which each domain value, or input, leads to exactly one range value, or output.
- Function notation is a shorthand method for relating the input to the output in the form [latex]y=f\left(x\right)[/latex].
- In tabular form, a function can be represented by rows or columns that relate to input and output values.
- To evaluate a function, we determine an output value for a corresponding input value. Algebraic forms of a function can be evaluated by replacing the input variable with a given value.
- To solve for a specific function value, we determine the input values that yield the specific output value.
- An algebraic form of a function can be written from an equation.
- Input and output values of a function can be identified from a table.
- Relating input values to output values on a graph is another way to evaluate a function.
- function is one-to-one if each output value corresponds to only one input value.
- A graph represents a function if any vertical line drawn on the graph intersects the graph at no more than one point.
- The graph of a one-to-one function passes the horizontal line test.
Glossary
- dependent variable
- an output variable
- domain
- the set of all possible input values for a relation
- function
- a relation in which each input value yields a unique output value
- horizontal line test
- a method of testing whether a function is one-to-one by determining whether any horizontal line intersects the graph more than once
- independent variable
- an input variable
- input
- each object or value in a domain that relates to another object or value by a relationship known as a function
- one-to-one function
- a function for which each value of the output is associated with a unique input value
- output
- each object or value in the range that is produced when an input value is entered into a function
- range
- the set of output values that result from the input values in a relation
- relation
- a set of ordered pairs
- vertical line test
- a method of testing whether a graph represents a function by determining whether a vertical line intersects the graph no more than once
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 111625, 111715, 11722. Provided by: Lumen Learning License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 111699. Provided by: Lumen Learning License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Determine if a Relation is a Function. Authored by: James Sousa. License: All Rights Reserved. License terms: Standard YouTube License.
- Function Notation Application. Authored by: James Sousa. License: CC BY: Attribution.
- Function Notation Application. Authored by: James Sousa. License: CC BY: Attribution.
- Question ID 2510, 1729. Authored by: Lippman, David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 15800. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 1647. Authored by: WebWork-Rochester, mb Lippman,David, mb Sousa,James. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 97486. Authored by: Carmichael, Patrick. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 15766, 2886, 3751. Authored by: Lippman, David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 40676. Authored by: Micheal Jenck. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
