Graphs of Polynomial Functions
The revenue in millions of dollars for a fictional cable company from 2006 through 2013 is shown in the table below.| Year | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| Revenues | 52.4 | 52.8 | 51.2 | 49.5 | 48.6 | 48.6 | 48.7 | 47.1 |
[latex]R\left(t\right)=-0.037{t}^{4}+1.414{t}^{3}-19.777{t}^{2}+118.696t - 205.332[/latex]
where R represents the revenue in millions of dollars and t represents the year, with t = 6 corresponding to 2006. Over which intervals is the revenue for the company increasing? Over which intervals is the revenue for the company decreasing? These questions, along with many others, can be answered by examining the graph of the polynomial function. We have already explored the local behavior of quadratics, a special case of polynomials. In this section we will explore the local behavior of polynomials in general.Multiplicity and Turning Points
Graphs behave differently at various x-intercepts. Sometimes, the graph will cross over the horizontal axis at an intercept. Other times, the graph will touch the horizontal axis and bounce off. Suppose, for example, we graph the function [latex]f\left(x\right)=\left(x+3\right){\left(x - 2\right)}^{2}{\left(x+1\right)}^{3}[/latex]. Notice in the figure below that the behavior of the function at each of the x-intercepts is different. Identifying the behavior of the graph at an x-intercept by examining the multiplicity of the zero.
Identifying the behavior of the graph at an x-intercept by examining the multiplicity of the zero.[latex]{\left(x - 2\right)}^{2}=\left(x - 2\right)\left(x - 2\right)[/latex]
The factor is repeated, that is, the factor [latex]\left(x - 2\right)[/latex] appears twice. The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity. The zero associated with this factor, [latex]x=2[/latex], has multiplicity 2 because the factor [latex]\left(x - 2\right)[/latex] occurs twice. The x-intercept [latex]x=-1[/latex] is the repeated solution of factor [latex]{\left(x+1\right)}^{3}=0[/latex]. The graph passes through the axis at the intercept, but flattens out a bit first. This factor is cubic (degree 3), so the behavior near the intercept is like that of a cubic—with the same S-shape near the intercept as the toolkit function [latex]f\left(x\right)={x}^{3}[/latex]. We call this a triple zero, or a zero with multiplicity 3. For zeros with even multiplicities, the graphs touch or are tangent to the x-axis. For zeros with odd multiplicities, the graphs cross or intersect the x-axis. See the figure below for examples of graphs of polynomial functions with multiplicity 1, 2, and 3. For higher even powers, such as 4, 6, and 8, the graph will still touch and bounce off of the horizontal axis but, for each increasing even power, the graph will appear flatter as it approaches and leaves the x-axis.
For higher odd powers, such as 5, 7, and 9, the graph will still cross through the horizontal axis, but for each increasing odd power, the graph will appear flatter as it approaches and leaves the x-axis.
For higher even powers, such as 4, 6, and 8, the graph will still touch and bounce off of the horizontal axis but, for each increasing even power, the graph will appear flatter as it approaches and leaves the x-axis.
For higher odd powers, such as 5, 7, and 9, the graph will still cross through the horizontal axis, but for each increasing odd power, the graph will appear flatter as it approaches and leaves the x-axis.
A General Note: Graphical Behavior of Polynomials at x-Intercepts
If a polynomial contains a factor of the form [latex]{\left(x-h\right)}^{p}[/latex], the behavior near the x-intercept h is determined by the power p. We say that [latex]x=h[/latex] is a zero of multiplicity p. The graph of a polynomial function will touch the x-axis at zeros with even multiplicities. The graph will cross the x-axis at zeros with odd multiplicities. The sum of the multiplicities is the degree of the polynomial function.How To: Given a graph of a polynomial function of degree n, identify the zeros and their multiplicities.
- If the graph crosses the x-axis and appears almost linear at the intercept, it is a single zero.
- If the graph touches the x-axis and bounces off of the axis, it is a zero with even multiplicity.
- If the graph crosses the x-axis at a zero, it is a zero with odd multiplicity.
- The sum of the multiplicities is n.
Example: Identifying Zeros and Their Multiplicities
Use the graph of the function of degree 6 to identify the zeros of the function and their possible multiplicities.
Answer: The polynomial function is of degree n. The sum of the multiplicities must be n. Starting from the left, the first zero occurs at [latex]x=-3[/latex]. The graph touches the x-axis, so the multiplicity of the zero must be even. The zero of –3 has multiplicity 2. The next zero occurs at [latex]x=-1[/latex]. The graph looks almost linear at this point. This is a single zero of multiplicity 1. The last zero occurs at [latex]x=4[/latex]. The graph crosses the x-axis, so the multiplicity of the zero must be odd. We know that the multiplicity is likely 3 and that the sum of the multiplicities is likely 6.
Try It
Use the graph of the function of degree 5 to identify the zeros of the function and their multiplicities.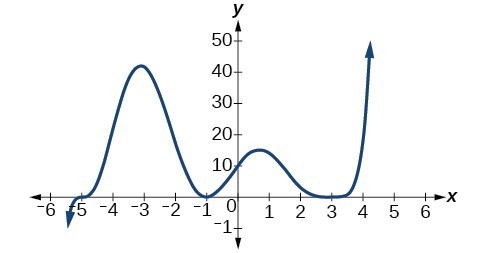
Answer: The graph has a zero of –5 with multiplicity 1, a zero of –1 with multiplicity 2, and a zero of 3 with even multiplicity.
The Intermediate Value Theorem
In some situations, we may know two points on a graph but not the zeros. If those two points are on opposite sides of the x-axis, we can confirm that there is a zero between them. Consider a polynomial function f whose graph is smooth and continuous. The Intermediate Value Theorem states that for two numbers a and b in the domain of f, if a < b and [latex]f\left(a\right)\ne f\left(b\right)[/latex], then the function f takes on every value between [latex]f\left(a\right)[/latex] and [latex]f\left(b\right)[/latex]. We can apply this theorem to a special case that is useful in graphing polynomial functions. If a point on the graph of a continuous function f at [latex]x=a[/latex] lies above the x-axis and another point at [latex]x=b[/latex] lies below the x-axis, there must exist a third point between [latex]x=a[/latex] and [latex]x=b[/latex] where the graph crosses the x-axis. Call this point [latex]\left(c,\text{ }f\left(c\right)\right)[/latex]. This means that we are assured there is a solution c where [latex]f\left(c\right)=0[/latex]. In other words, the Intermediate Value Theorem tells us that when a polynomial function changes from a negative value to a positive value, the function must cross the x-axis. The figure below shows that there is a zero between a and b.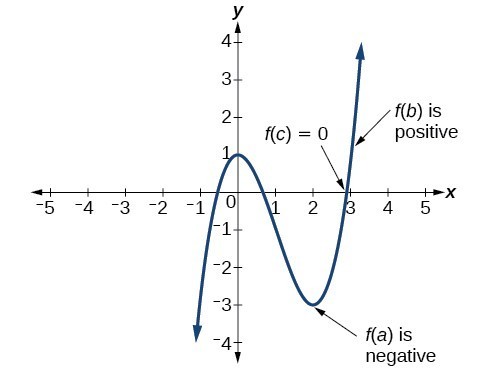 Using the Intermediate Value Theorem to show there exists a zero.
Using the Intermediate Value Theorem to show there exists a zero.A General Note: Intermediate Value Theorem
Let f be a polynomial function. The Intermediate Value Theorem states that if [latex]f\left(a\right)[/latex] and [latex]f\left(b\right)[/latex] have opposite signs, then there exists at least one value c between a and b for which [latex]f\left(c\right)=0[/latex].Example: Using the Intermediate Value Theorem
Show that the function [latex]f\left(x\right)={x}^{3}-5{x}^{2}+3x+6[/latex] has at least two real zeros between [latex]x=1[/latex] and [latex]x=4[/latex].Answer: As a start, evaluate [latex]f\left(x\right)[/latex] at the integer values [latex]x=1,2,3,\text{ and }4[/latex].
| x | 1 | 2 | 3 | 4 |
| f (x) | 5 | 0 | –3 | 2 |
Analysis of the Solution
We can also see that there are two real zeros between [latex]x=1[/latex] and [latex]x=4[/latex].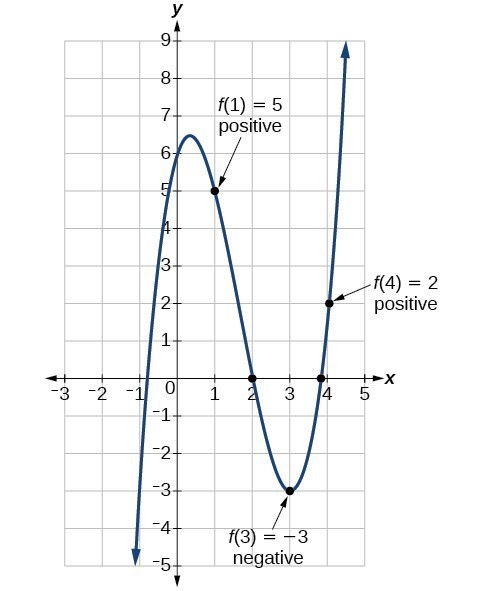
Try It
Show that the function [latex]f\left(x\right)=7{x}^{5}-9{x}^{4}-{x}^{2}[/latex] has at least one real zero between [latex]x=1[/latex] and [latex]x=2[/latex].Answer: Because f is a polynomial function and since [latex]f\left(1\right)[/latex] is negative and [latex]f\left(2\right)[/latex] is positive, there is at least one real zero between [latex]x=1[/latex] and [latex]x=2[/latex].
Writing Formulas for Polynomial Functions
Now that we know how to find zeros of polynomial functions, we can use them to write formulas based on graphs. Because a polynomial function written in factored form will have an x-intercept where each factor is equal to zero, we can form a function that will pass through a set of x-intercepts by introducing a corresponding set of factors.A General Note: Factored Form of Polynomials
If a polynomial of lowest degree p has horizontal intercepts at [latex]x={x}_{1},{x}_{2},\dots ,{x}_{n}[/latex], then the polynomial can be written in the factored form: [latex]f\left(x\right)=a{\left(x-{x}_{1}\right)}^{{p}_{1}}{\left(x-{x}_{2}\right)}^{{p}_{2}}\cdots {\left(x-{x}_{n}\right)}^{{p}_{n}}[/latex] where the powers [latex]{p}_{i}[/latex] on each factor can be determined by the behavior of the graph at the corresponding intercept, and the stretch factor a can be determined given a value of the function other than the x-intercept.How To: Given a graph of a polynomial function, write a formula for the function.
- Identify the x-intercepts of the graph to find the factors of the polynomial.
- Examine the behavior of the graph at the x-intercepts to determine the multiplicity of each factor.
- Find the polynomial of least degree containing all the factors found in the previous step.
- Use any other point on the graph (the y-intercept may be easiest) to determine the stretch factor.
Example: Writing a Formula for a Polynomial Function from the Graph
Write a formula for the polynomial function.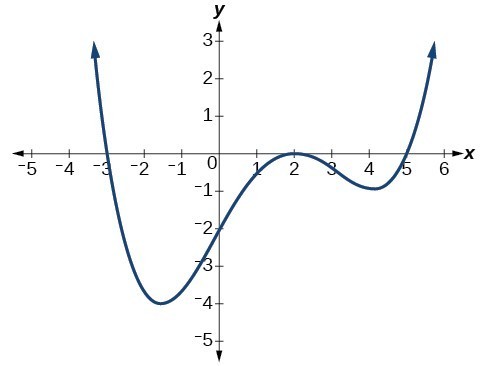
Answer: This graph has three x-intercepts: x = –3, 2, and 5. The y-intercept is located at (0, 2). At x = –3 and x = 5, the graph passes through the axis linearly, suggesting the corresponding factors of the polynomial will be linear. At x = 2, the graph bounces at the intercept, suggesting the corresponding factor of the polynomial will be second degree (quadratic). Together, this gives us [latex-display]f\left(x\right)=a\left(x+3\right){\left(x - 2\right)}^{2}\left(x - 5\right)[/latex-display] To determine the stretch factor, we utilize another point on the graph. We will use the y-intercept (0, –2), to solve for a. [latex-display]\begin{array}{l}f\left(0\right)=a\left(0+3\right){\left(0 - 2\right)}^{2}\left(0 - 5\right)\hfill \\ \text{ }-2=a\left(0+3\right){\left(0 - 2\right)}^{2}\left(0 - 5\right)\hfill \\ \text{ }-2=-60a\hfill \\ \text{ }a=\frac{1}{30}\hfill \end{array}[/latex-display] The graphed polynomial appears to represent the function [latex]f\left(x\right)=\frac{1}{30}\left(x+3\right){\left(x - 2\right)}^{2}\left(x - 5\right)[/latex].
Try It 5
Given the graph below, write a formula for the function shown.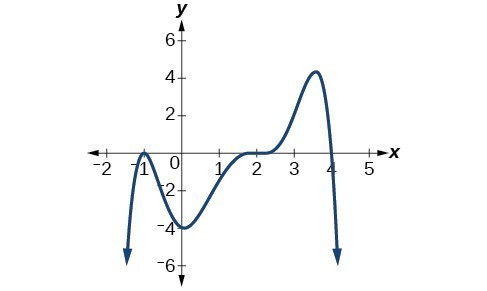
Answer: [latex]f\left(x\right)=-\frac{1}{8}{\left(x - 2\right)}^{3}{\left(x+1\right)}^{2}\left(x - 4\right)[/latex]
Using Local and Global Extrema
With quadratics, we were able to algebraically find the maximum or minimum value of the function by finding the vertex. For general polynomials, finding these turning points is not possible without more advanced techniques from calculus. Even then, finding where extrema occur can still be algebraically challenging. For now, we will estimate the locations of turning points using technology to generate a graph. Each turning point represents a local minimum or maximum. Sometimes, a turning point is the highest or lowest point on the entire graph. In these cases, we say that the turning point is a global maximum or a global minimum. These are also referred to as the absolute maximum and absolute minimum values of the function.Local and Global Extrema
A local maximum or local minimum at x = a (sometimes called the relative maximum or minimum, respectively) is the output at the highest or lowest point on the graph in an open interval around x = a. If a function has a local maximum at a, then [latex]f\left(a\right)\ge f\left(x\right)[/latex] for all x in an open interval around x = a. If a function has a local minimum at a, then [latex]f\left(a\right)\le f\left(x\right)[/latex] for all x in an open interval around x = a. A global maximum or global minimum is the output at the highest or lowest point of the function. If a function has a global maximum at a, then [latex]f\left(a\right)\ge f\left(x\right)[/latex] for all x. If a function has a global minimum at a, then [latex]f\left(a\right)\le f\left(x\right)[/latex] for all x. We can see the difference between local and global extrema below.
Q & A
Do all polynomial functions have a global minimum or maximum? No. Only polynomial functions of even degree have a global minimum or maximum. For example, [latex]f\left(x\right)=x[/latex] has neither a global maximum nor a global minimum.Example: Using Local Extrema to Solve Applications
An open-top box is to be constructed by cutting out squares from each corner of a 14 cm by 20 cm sheet of plastic then folding up the sides. Find the size of squares that should be cut out to maximize the volume enclosed by the box.Answer:
We will start this problem by drawing a picture like the one below, labeling the width of the cut-out squares with a variable, w.
 Notice that after a square is cut out from each end, it leaves a [latex]\left(14 - 2w\right)[/latex] cm by [latex]\left(20 - 2w\right)[/latex] cm rectangle for the base of the box, and the box will be w cm tall. This gives the volume
[latex-display]\begin{array}{l}V\left(w\right)=\left(20 - 2w\right)\left(14 - 2w\right)w\hfill \\ \text{ }=280w - 68{w}^{2}+4{w}^{3}\hfill \end{array}[/latex-display]
Notice that after a square is cut out from each end, it leaves a [latex]\left(14 - 2w\right)[/latex] cm by [latex]\left(20 - 2w\right)[/latex] cm rectangle for the base of the box, and the box will be w cm tall. This gives the volume
[latex-display]\begin{array}{l}V\left(w\right)=\left(20 - 2w\right)\left(14 - 2w\right)w\hfill \\ \text{ }=280w - 68{w}^{2}+4{w}^{3}\hfill \end{array}[/latex-display]
 Notice, since the factors are w, [latex]20 - 2w[/latex] and [latex]14 - 2w[/latex], the three zeros are 10, 7, and 0, respectively. Because a height of 0 cm is not reasonable, we consider the only the zeros 10 and 7. The shortest side is 14 and we are cutting off two squares, so values w may take on are greater than zero or less than 7. This means we will restrict the domain of this function to [latex]0<w<7[/latex]. Using technology to sketch the graph of [latex]V\left(w\right)[/latex] on this reasonable domain, we get a graph like Figure 24. We can use this graph to estimate the maximum value for the volume, restricted to values for w that are reasonable for this problem—values from 0 to 7.
From this graph, we turn our focus to only the portion on the reasonable domain, [latex]\left[0,\text{ }7\right][/latex]. We can estimate the maximum value to be around 340 cubic cm, which occurs when the squares are about 2.75 cm on each side. To improve this estimate, we could use advanced features of our technology, if available, or simply change our window to zoom in on our graph to produce the graph below.
Notice, since the factors are w, [latex]20 - 2w[/latex] and [latex]14 - 2w[/latex], the three zeros are 10, 7, and 0, respectively. Because a height of 0 cm is not reasonable, we consider the only the zeros 10 and 7. The shortest side is 14 and we are cutting off two squares, so values w may take on are greater than zero or less than 7. This means we will restrict the domain of this function to [latex]0<w<7[/latex]. Using technology to sketch the graph of [latex]V\left(w\right)[/latex] on this reasonable domain, we get a graph like Figure 24. We can use this graph to estimate the maximum value for the volume, restricted to values for w that are reasonable for this problem—values from 0 to 7.
From this graph, we turn our focus to only the portion on the reasonable domain, [latex]\left[0,\text{ }7\right][/latex]. We can estimate the maximum value to be around 340 cubic cm, which occurs when the squares are about 2.75 cm on each side. To improve this estimate, we could use advanced features of our technology, if available, or simply change our window to zoom in on our graph to produce the graph below.
![Graph of V(w)=(20-2w)(14-2w)w where the x-axis is labeled w and the y-axis is labeled V(w) on the domain [2.4, 3].](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/896/2016/11/02201637/CNX_Precalc_Figure_03_04_0292.jpg) From this zoomed-in view, we can refine our estimate for the maximum volume to about 339 cubic cm, when the squares measure approximately 2.7 cm on each side.
From this zoomed-in view, we can refine our estimate for the maximum volume to about 339 cubic cm, when the squares measure approximately 2.7 cm on each side.
Key Concepts
- Polynomial functions of degree 2 or more are smooth, continuous functions.
- To find the zeros of a polynomial function, if it can be factored, factor the function and set each factor equal to zero.
- Another way to find the x-intercepts of a polynomial function is to graph the function and identify the points at which the graph crosses the x-axis.
- The multiplicity of a zero determines how the graph behaves at the x-intercepts.
- The graph of a polynomial will cross the horizontal axis at a zero with odd multiplicity.
- The graph of a polynomial will touch the horizontal axis at a zero with even multiplicity.
- The end behavior of a polynomial function depends on the leading term.
- The graph of a polynomial function changes direction at its turning points.
- A polynomial function of degree n has at most n – 1 turning points.
- To graph polynomial functions, find the zeros and their multiplicities, determine the end behavior, and ensure that the final graph has at most n – 1 turning points.
- Graphing a polynomial function helps to estimate local and global extremas.
- The Intermediate Value Theorem tells us that if [latex]f\left(a\right) \text{and} f\left(b\right)[/latex] have opposite signs, then there exists at least one value c between a and b for which [latex]f\left(c\right)=0[/latex].
Glossary
global maximum highest turning point on a graph; [latex]f\left(a\right)[/latex] where [latex]f\left(a\right)\ge f\left(x\right)[/latex] for all x. global minimum lowest turning point on a graph; [latex]f\left(a\right)[/latex] where [latex]f\left(a\right)\le f\left(x\right)[/latex] for all x. Intermediate Value Theorem for two numbers a and b in the domain of f, if [latex]a<b[/latex] and [latex]f\left(a\right)\ne f\left(b\right)[/latex], then the function f takes on every value between [latex]f\left(a\right)[/latex] and [latex]f\left(b\right)[/latex]; specifically, when a polynomial function changes from a negative value to a positive value, the function must cross the x-axis multiplicity the number of times a given factor appears in the factored form of the equation of a polynomial; if a polynomial contains a factor of the form [latex]{\left(x-h\right)}^{p}[/latex], [latex]x=h[/latex] is a zero of multiplicity p.Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 121830. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 29470, 29478. Authored by: Caren McClure. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
