We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Write the point-slope form of an equation

Up until now, we have been using the slope-intercept form of a linear equation to describe linear functions. Here, we will learn another way to write a linear function, the point-slope form.

[latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]

The point-slope form is derived from the slope formula.

[latex]\begin{cases}{m}=\frac{y-{y}_{1}}{x-{x}_{1}}\hfill & \text{assuming }{ x }\ne {x}_{1}\hfill\\{ m }\left(x-{x}_{1}\right)=\frac{y-{y}_{1}}{x-{x}_{1}}\left(x-{x}_{1}\right)\hfill & \text{Multiply both sides by }\left(x-{x}_{1}\right)\hfill\\{ m }\left(x-{x}_{1}\right)=y-{y}_{1}\hfill & \text{Simplify}\hfill \\ y-{y}_{1}={ m }\left(x-{x}_{1}\right)\hfill &\text{Rearrange}\hfill \end{cases}[/latex]

Keep in mind that the slope-intercept form and the point-slope form can be used to describe the same function. We can move from one form to another using basic algebra. For example, suppose we are given an equation in point-slope form, [latex]y - 4=-\frac{1}{2}\left(x - 6\right)[/latex] . We can convert it to the slope-intercept form as shown.

[latex]\begin{cases}y - 4=-\frac{1}{2}\left(x - 6\right)\hfill & \hfill \\ y - 4=-\frac{1}{2}x+3\hfill & \text{Distribute the }-\frac{1}{2}.\hfill \\ \text{ }y=-\frac{1}{2}x+7\hfill & \text{Add 4 to each side}.\hfill \end{cases}[/latex]

Therefore, the same line can be described in slope-intercept form as [latex]y=-\frac{1}{2}x+7[/latex].

A General Note: Point-Slope Form of a Linear Equation

The point-slope form of a linear equation takes the form

[latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]

where [latex]m[/latex] is the slope, [latex]{x}_{1 }\text{and} {y}_{1}[/latex] are the [latex]x\text{ and }y[/latex] coordinates of a specific point through which the line passes.

Writing the Equation of a Line Using a Point and the Slope

The point-slope form is particularly useful if we know one point and the slope of a line. Suppose, for example, we are told that a line has a slope of 2 and passes through the point [latex]\left(4,1\right)[/latex]. We know that [latex]m=2[/latex] and that [latex]{x}_{1}=4[/latex] and [latex]{y}_{1}=1[/latex]. We can substitute these values into the general point-slope equation.

[latex]\begin{cases}y-{y}_{1}=m\left(x-{x}_{1}\right)\\ y - 1=2\left(x - 4\right)\end{cases}[/latex]

If we wanted to then rewrite the equation in slope-intercept form, we apply algebraic techniques.

[latex]\begin{cases}y - 1=2\left(x - 4\right)\hfill & \hfill \\ y - 1=2x - 8\hfill & \text{Distribute the }2.\hfill \\ \text{ }y=2x - 7\hfill & \text{Add 1 to each side}.\hfill \end{cases}[/latex]

Both equations, [latex]y - 1=2\left(x - 4\right)[/latex] and [latex]y=2x - 7[/latex], describe the same line. See Figure 6.

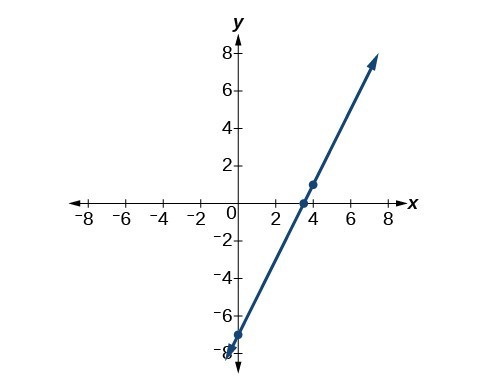Figure 6

Example 5: Writing Linear Equations Using a Point and the Slope

Write the point-slope form of an equation of a line with a slope of 3 that passes through the point [latex]\left(6,-1\right)[/latex]. Then rewrite it in the slope-intercept form.

Solution

Let’s figure out what we know from the given information. The slope is 3, so m = 3. We also know one point, so we know [latex]{x}_{1}=6[/latex] and [latex]{y}_{1}=-1[/latex]. Now we can substitute these values into the general point-slope equation.

[latex]\begin{cases}\text{ }y-{y}_{1}=m\left(x-{x}_{1}\right)\hfill & \hfill \\ y-\left(-1\right)=3\left(x - 6\right)\hfill & \text{Substitute known values}.\hfill \\ \text{ }y+1=3\left(x - 6\right)\hfill & \text{Distribute }-1\text{ to find point-slope form}.\hfill \end{cases}[/latex]

Then we use algebra to find the slope-intercept form.

[latex]\begin{cases}y+1=3\left(x - 6\right)\hfill & \hfill \\ y+1=3x - 18\hfill & \text{Distribute 3}.\hfill \\ \text{ }y=3x - 19\hfill & \text{Simplify to slope-intercept form}.\hfill \end{cases}[/latex]

Try It 3

Write the point-slope form of an equation of a line with a slope of –2 that passes through the point [latex]\left(-2,\text{ }2\right)[/latex]. Then rewrite it in the slope-intercept form.

Solution

Writing the Equation of a Line Using Two Points

The point-slope form of an equation is also useful if we know any two points through which a line passes. Suppose, for example, we know that a line passes through the points [latex]\left(0,\text{ }1\right)[/latex] and [latex]\left(3,\text{ }2\right)[/latex]. We can use the coordinates of the two points to find the slope.

[latex]\begin{cases}{m}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\\ \text{ }=\frac{2 - 1}{3 - 0}\hfill \\ \text{ }=\frac{1}{3}\hfill \end{cases}[/latex]

Now we can use the slope we found and the coordinates of one of the points to find the equation for the line. Let use (0, 1) for our point.

[latex]\begin{cases}y-{y}_{1}=m\left(x-{x}_{1}\right)\\ y - 1=\frac{1}{3}\left(x - 0\right)\end{cases}[/latex]

As before, we can use algebra to rewrite the equation in the slope-intercept form.

[latex]\begin{cases}y - 1=\frac{1}{3}\left(x - 0\right)\hfill & \hfill \\ y - 1=\frac{1}{3}x\hfill & \text{Distribute the }\frac{1}{3}.\hfill \\ \text{ }y=\frac{1}{3}x+1\hfill & \text{Add 1 to each side}.\hfill \end{cases}[/latex]

Both equations describe the line shown in Figure 7.

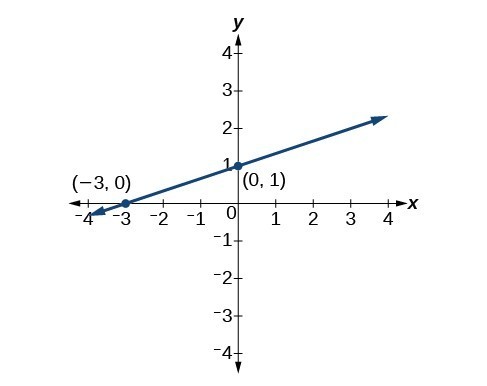Figure 7

Example 6: Writing Linear Equations Using Two Points

Write the point-slope form of an equation of a line that passes through the points (5, 1) and (8, 7). Then rewrite it in the slope-intercept form.

Solution

Let’s begin by finding the slope.

[latex]\begin{cases}{m}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\hfill \\ \text{ }=\frac{7 - 1}{8 - 5}\hfill \\ \text{ }=\frac{6}{3}\hfill \\ \text{ }=2\hfill \end{cases}[/latex]

So [latex]m=2[/latex]. Next, we substitute the slope and the coordinates for one of the points into the general point-slope equation. We can choose either point, but we will use [latex]\left(5,1\right)[/latex].

[latex]\begin{cases}y-{y}_{1}=m\left(x-{x}_{1}\right)\\ y - 1=2\left(x - 5\right)\end{cases}[/latex]

The point-slope equation of the line is [latex]{y}_{2}-1=2\left({x}_{2}-5\right)[/latex]. To rewrite the equation in slope-intercept form, we use algebra.

[latex]\begin{cases}y - 1=2\left(x - 5\right)\hfill \\ y - 1=2x - 10\hfill \\ \text{ }y=2x - 9\hfill \end{cases}[/latex]

The slope-intercept equation of the line is [latex]y=2x - 9[/latex].

Try It 4

Write the point-slope form of an equation of a line that passes through the points [latex]\left(-1,3\right)\\ [/latex] and [latex]\left(0,0\right)[/latex]. Then rewrite it in the slope-intercept form.

Solution

Licenses & Attributions

CC licensed content, Shared previously

  • Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..