Write the equation of a line parallel or perpendicular to a given line
If we know the equation of a line, we can use what we know about slope to write the equation of a line that is either parallel or perpendicular to the given line.
Writing Equations of Parallel Lines
Suppose for example, we are given the following equation.
We know that the slope of the line formed by the function is 3. We also know that the y-intercept is (0, 1). Any other line with a slope of 3 will be parallel to f(x). So the lines formed by all of the following functions will be parallel to f(x).
Suppose then we want to write the equation of a line that is parallel to f and passes through the point (1, 7). We already know that the slope is 3. We just need to determine which value for b will give the correct line. We can begin with the point-slope form of an equation for a line, and then rewrite it in the slope-intercept form.
So [latex]g\left(x\right)=3x+4[/latex] is parallel to [latex]f\left(x\right)=3x+1[/latex] and passes through the point (1, 7).
How To: Given the equation of a function and a point through which its graph passes, write the equation of a line parallel to the given line that passes through the given point.
- Find the slope of the function.
- Substitute the given values into either the general point-slope equation or the slope-intercept equation for a line.
- Simplify.
Example 9: Finding a Line Parallel to a Given Line
Find a line parallel to the graph of [latex]f\left(x\right)=3x+6[/latex] that passes through the point (3, 0).
Solutions
The slope of the given line is 3. If we choose the slope-intercept form, we can substitute m = 3, x = 3, and f(x) = 0 into the slope-intercept form to find the y-intercept.
The line parallel to f(x) that passes through (3, 0) is [latex]g\left(x\right)=3x - 9[/latex].
Writing Equations of Perpendicular Lines
We can use a very similar process to write the equation for a line perpendicular to a given line. Instead of using the same slope, however, we use the negative reciprocal of the given slope. Suppose we are given the following function:
The slope of the line is 2, and its negative reciprocal is [latex]-\frac{1}{2}[/latex]. Any function with a slope of [latex]-\frac{1}{2}[/latex] will be perpendicular to f(x). So the lines formed by all of the following functions will be perpendicular to f(x).
As before, we can narrow down our choices for a particular perpendicular line if we know that it passes through a given point. Suppose then we want to write the equation of a line that is perpendicular to f(x) and passes through the point (4, 0). We already know that the slope is [latex]-\frac{1}{2}[/latex]. Now we can use the point to find the y-intercept by substituting the given values into the slope-intercept form of a line and solving for b.
The equation for the function with a slope of [latex]-\frac{1}{2}[/latex] and a y-intercept of 2 is
So [latex]g\left(x\right)=-\frac{1}{2}x+2[/latex] is perpendicular to [latex]f\left(x\right)=2x+4[/latex] and passes through the point (4, 0). Be aware that perpendicular lines may not look obviously perpendicular on a graphing calculator unless we use the square zoom feature.
Q & A
A horizontal line has a slope of zero and a vertical line has an undefined slope. These two lines are perpendicular, but the product of their slopes is not –1. Doesn’t this fact contradict the definition of perpendicular lines?
No. For two perpendicular linear functions, the product of their slopes is –1. However, a vertical line is not a function so the definition is not contradicted.
How To: Given the equation of a function and a point through which its graph passes, write the equation of a line perpendicular to the given line.
- Find the slope of the function.
- Determine the negative reciprocal of the slope.
- Substitute the new slope and the values for x and y from the coordinate pair provided into [latex]g\left(x\right)=mx+b[/latex].
- Solve for b.
- Write the equation for the line.
Example 10: Finding the Equation of a Perpendicular Line
Find the equation of a line perpendicular to [latex]f\left(x\right)=3x+3[/latex] that passes through the point (3, 0).
Solution
The original line has slope m = 3, so the slope of the perpendicular line will be its negative reciprocal, or [latex]-\frac{1}{3}[/latex]. Using this slope and the given point, we can find the equation for the line.
The line perpendicular to f(x) that passes through (3, 0) is [latex]g\left(x\right)=-\frac{1}{3}x+1[/latex].
Analysis of the Solution
A graph of the two lines is shown in Figure 23.
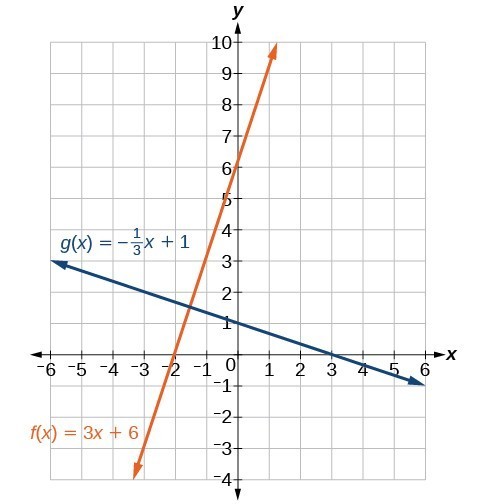 Figure 23
Figure 23Try It 5
Given the function [latex]h\left(x\right)=2x - 4[/latex], write an equation for the line passing through (0, 0) that is
a. parallel to h(x) b. perpendicular to h(x)
SolutionHow To: Given two points on a line and a third point, write the equation of the perpendicular line that passes through the point.
- Determine the slope of the line passing through the points.
- Find the negative reciprocal of the slope.
- Use the slope-intercept form or point-slope form to write the equation by substituting the known values.
- Simplify.
Example 11: Finding the Equation of a Line Perpendicular to a Given Line Passing through a Point
A line passes through the points (–2, 6) and (4, 5). Find the equation of a perpendicular line that passes through the point (4, 5).
Solution
From the two points of the given line, we can calculate the slope of that line.Find the negative reciprocal of the slope.
We can then solve for the y-intercept of the line passing through the point (4, 5).
The equation for the line that is perpendicular to the line passing through the two given points and also passes through point (4, 5) is
Try It 6
A line passes through the points, (–2, –15) and (2, –3). Find the equation of a perpendicular line that passes through the point, (6, 4).
SolutionLicenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..

Analysis of the Solution
We can confirm that the two lines are parallel by graphing them. Figure 22 shows that the two lines will never intersect.