We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

학습 가이드 > College Algebra

Introduction to Polynomials

Learning Objectives

By the end of this section, you will be able to:
  • Identify the degree and leading coefficient of polynomials.
  • Add and subtract polynomials.
  • Multiply polynomials.
  • Use FOIL to multiply binomials.
  • Perform operations with polynomials of several variables.
Earl is building a doghouse, whose front is in the shape of a square topped with a triangle. There will be a rectangular door through which the dog can enter and exit the house. Earl wants to find the area of the front of the doghouse so that he can purchase the correct amount of paint. Using the measurements of the front of the house, shown in Figure 1, we can create an expression that combines several variable terms, allowing us to solve this problem and others like it.
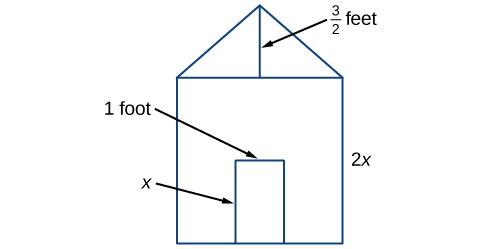Sketch of a house formed by a square and a triangle based on the top of the square. A rectangle is placed at the bottom center of the square to mark a doorway. The height of the door is labeled: x and the width of the door is labeled: 1 foot. The side of the square is labeled: 2x. The height of the triangle is labeled: 3/2 feet. Figure 1
First find the area of the square in square feet.
[latex]\begin{array}{ccc}\hfill A& =& {s}^{2}\hfill \\ & =& {\left(2x\right)}^{2}\hfill \\ & =& 4{x}^{2}\hfill \end{array}[/latex]
Then find the area of the triangle in square feet.
[latex]\begin{array}{ccc}\hfill A& =& \frac{1}{2}bh\hfill \\ & =& \text{ }\frac{1}{2}\left(2x\right)\left(\frac{3}{2}\right)\hfill \\ & =& \text{ }\frac{3}{2}x\hfill \end{array}[/latex]
Next find the area of the rectangular door in square feet.
[latex]\begin{array}{ccc}\hfill A& =& lw\hfill \\ & =& x\cdot 1\hfill \\ \hfill & =& x\hfill \end{array}[/latex]
The area of the front of the doghouse can be found by adding the areas of the square and the triangle, and then subtracting the area of the rectangle. When we do this, we get [latex]4{x}^{2}+\frac{3}{2}x-x{\text{ft}}^{2}[/latex], or [latex]4{x}^{2}+\frac{1}{2}x[/latex] ft2. In this section, we will examine expressions such as this one, which combine several variable terms.

Licenses & Attributions

CC licensed content, Specific attribution