Create a new function by composition of functions
Performing algebraic operations on functions combines them into a new function, but we can also create functions by composing functions. When we wanted to compute a heating cost from a day of the year, we created a new function that takes a day as input and yields a cost as output. The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. The resulting function is known as a composite function. We represent this combination by the following notation:
[latex]\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)[/latex]
We read the left-hand side as [latex]"f[/latex] composed with [latex]g[/latex] at [latex]x,"[/latex] and the right-hand side as [latex]"f[/latex] of [latex]g[/latex] of [latex]x."[/latex] The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol [latex]\circ [/latex] is called the composition operator. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value. Composition is a binary operation that takes two functions and forms a new function, much as addition or multiplication takes two numbers and gives a new number. However, it is important not to confuse function composition with multiplication because, as we learned above, in most cases [latex]f\left(g\left(x\right)\right)\ne f\left(x\right)g\left(x\right)[/latex]. It is also important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside. In the equation above, the function [latex]g[/latex] takes the input [latex]x[/latex] first and yields an output [latex]g\left(x\right)[/latex]. Then the function [latex]f[/latex] takes [latex]g\left(x\right)[/latex] as an input and yields an output [latex]f\left(g\left(x\right)\right)[/latex].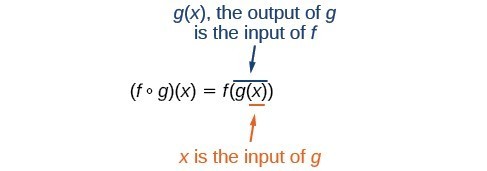 Figure 2
Figure 2[latex]\begin{cases}\text{ }f\left(g\left(x\right)\right)=f\left(x+2\right)\hfill \\ \text{ }={\left(x+2\right)}^{2}\hfill \\ \text{ }={x}^{2}+4x+4\hfill \end{cases}[/latex]
but
[latex]\begin{cases}\text{ }g\left(f\left(x\right)\right)=g\left({x}^{2}\right)\hfill \\ \text{ }={x}^{2}+2\hfill \end{cases}[/latex]
These expressions are not equal for all values of [latex]x[/latex], so the two functions are not equal. It is irrelevant that the expressions happen to be equal for the single input value [latex]x=-\frac{1}{2}[/latex]. Note that the range of the inside function (the first function to be evaluated) needs to be within the domain of the outside function. Less formally, the composition has to make sense in terms of inputs and outputs.A General Note: Composition of Functions
When the output of one function is used as the input of another, we call the entire operation a composition of functions. For any input [latex]x[/latex] and functions [latex]f[/latex] and [latex]g[/latex], this action defines a composite function, which we write as [latex]f\circ g[/latex] such that[latex]\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)[/latex]
The domain of the composite function [latex]f\circ g[/latex] is all [latex]x[/latex] such that [latex]x[/latex] is in the domain of [latex]g[/latex] and [latex]g\left(x\right)[/latex] is in the domain of [latex]f[/latex]. It is important to realize that the product of functions [latex]fg[/latex] is not the same as the function composition [latex]f\left(g\left(x\right)\right)[/latex], because, in general, [latex]f\left(x\right)g\left(x\right)\ne f\left(g\left(x\right)\right)[/latex].Example 2: Determining whether Composition of Functions is Commutative
Using the functions provided, find [latex]f\left(g\left(x\right)\right)[/latex] and [latex]g\left(f\left(x\right)\right)[/latex]. Determine whether the composition of the functions is commutative.Solution
[latex]f\left(x\right)=2x+1g\left(x\right)=3-x[/latex]
Let’s begin by substituting [latex]g\left(x\right)[/latex] into [latex]f\left(x\right)[/latex].[latex]\begin{cases}f\left(g\left(x\right)\right)=2\left(3-x\right)+1\hfill \\ \text{ }=6 - 2x+1\hfill \\ \text{ }=7 - 2x\hfill \end{cases}[/latex] Now we can substitute [latex]f\left(x\right)[/latex] into [latex]g\left(x\right)[/latex].[latex]\begin{cases}g\left(f\left(x\right)\right)=3-\left(2x+1\right)\hfill \\ \text{ }=3 - 2x - 1\hfill \\ \text{ }=-2x+2\hfill \end{cases}[/latex]
We find that [latex]g\left(f\left(x\right)\right)\ne f\left(g\left(x\right)\right)[/latex], so the operation of function composition is not commutative.Example 3: Interpreting Composite Functions
The function [latex]c\left(s\right)[/latex] gives the number of calories burned completing [latex]s[/latex] sit-ups, and [latex]s\left(t\right)[/latex] gives the number of sit-ups a person can complete in [latex]t[/latex] minutes. Interpret [latex]c\left(s\left(3\right)\right)[/latex].Solution
The inside expression in the composition is [latex]s\left(3\right)[/latex]. Because the input to the s-function is time, [latex]t=3[/latex] represents 3 minutes, and [latex]s\left(3\right)[/latex] is the number of sit-ups completed in 3 minutes. Using [latex]s\left(3\right)[/latex] as the input to the function [latex]c\left(s\right)[/latex] gives us the number of calories burned during the number of sit-ups that can be completed in 3 minutes, or simply the number of calories burned in 3 minutes (by doing sit-ups).Example 4: Investigating the Order of Function Composition
Suppose [latex]f\left(x\right)[/latex] gives miles that can be driven in [latex]x[/latex] hours and [latex]g\left(y\right)[/latex] gives the gallons of gas used in driving [latex]y[/latex] miles. Which of these expressions is meaningful: [latex]f\left(g\left(y\right)\right)[/latex] or [latex]g\left(f\left(x\right)\right)?[/latex]Solution
The function [latex]y=f\left(x\right)[/latex] is a function whose output is the number of miles driven corresponding to the number of hours driven.[latex]\text{number of miles }=f\left(\text{number of hours}\right)[/latex]
The function [latex]g\left(y\right)[/latex] is a function whose output is the number of gallons used corresponding to the number of miles driven. This means:[latex]\text{number of gallons }=g\left(\text{number of miles}\right)[/latex]
The expression [latex]g\left(y\right)[/latex] takes miles as the input and a number of gallons as the output. The function [latex]f\left(x\right)[/latex] requires a number of hours as the input. Trying to input a number of gallons does not make sense. The expression [latex]f\left(g\left(y\right)\right)[/latex] is meaningless. The expression [latex]f\left(x\right)[/latex] takes hours as input and a number of miles driven as the output. The function [latex]g\left(y\right)[/latex] requires a number of miles as the input. Using [latex]f\left(x\right)[/latex] (miles driven) as an input value for [latex]g\left(y\right)[/latex], where gallons of gas depends on miles driven, does make sense. The expression [latex]g\left(f\left(x\right)\right)[/latex] makes sense, and will yield the number of gallons of gas used, [latex]g[/latex], driving a certain number of miles, [latex]f\left(x\right)[/latex], in [latex]x[/latex] hours.Q & A
Are there any situations where [latex]f\left(g\left(y\right)\right)[/latex] and [latex]g\left(f\left(x\right)\right)[/latex] would both be meaningful or useful expressions? Yes. For many pure mathematical functions, both compositions make sense, even though they usually produce different new functions. In real-world problems, functions whose inputs and outputs have the same units also may give compositions that are meaningful in either order.Try It 2
The gravitational force on a planet a distance r from the sun is given by the function [latex]G\left(r\right)[/latex]. The acceleration of a planet subjected to any force [latex]F[/latex] is given by the function [latex]a\left(F\right)[/latex]. Form a meaningful composition of these two functions, and explain what it means. SolutionLicenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
