We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

8B.1 Algebraic Operations on Polynomials

8B.1 Learning Objectives

  • Anatomy of a polynomial
    • Identify the degree and leading coefficient of a polynomial
    • Evaluate a polynomial for given values
  • Sums and Products of Polynomials
    • Add and subtract polynomials
    • Find the product of polynomials
    • Find the product of two binomials using the FOIL method
  • Multiply a Trinomial and a Binomial
  • Divide Polynomials
    • Divide a polynomials using long division
    • Divide polynomials using synthetic division
In the example on the previous page, we saw how combining the formulas for different shapes provides a way to accurately predict the amount of paint needed for a construction project. The result was a polynomial. A polynomial function is a function consisting of sum or difference of terms in which each term is a real number, a variable, or the product of a real number and variables with an non-negative integer exponents. Non negative integers are 0, 1, 2, 3, 4, ... You may see a resemblance between expressions and polynomials, which we have been studying in this course.  Polynomials are a special sub-group of mathematical expressions and equations. The following table is intended to help you tell the difference between what is a polynomial and what is not.
IS a Polynomial Is NOT a Polynomial Because
[latex]2x^2-\frac{1}{2}x -9[/latex] [latex]\frac{2}{x^{2}}+x[/latex] Polynomials only have variables in the numerator
[latex]\frac{y}{4}-y^3[/latex] [latex]\frac{2}{y}+4[/latex] Polynomials only have variables in the numerator
[latex]\sqrt{12}\left(a\right)+9[/latex]  [latex]\sqrt{a}+7[/latex] Roots are equivalent to rational exponents, and polynomials only have integer exponents
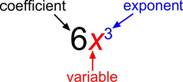The basic building block of a polynomial is a monomial. A monomial is one term and can be a number, a variable, or the product of a number and variables with an exponent. The number part of the term is called the coefficient. The expression 6x to the power of 3. 6 is the coefficient, x is the variable, and the power of 3 is the exponent. A polynomial containing two terms, such as [latex]2x - 9[/latex], is called a binomial. A polynomial containing three terms, such as [latex]-3{x}^{2}+8x - 7[/latex], is called a trinomial. We can find the degree of a polynomial by identifying the highest power of the variable that occurs in the polynomial. The term with the highest degree is called the leading term because it is usually written first. The coefficient of the leading term is called the leading coefficient. When a polynomial is written so that the powers are descending, we say that it is in standard form. It is important to note that polynomials only have integer exponents. 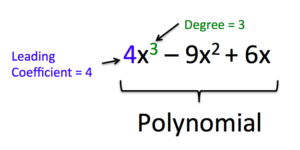4x^3 - 9x^2 + 6x, with the text

Given a polynomial expression, identify the degree and leading coefficient.

  1. Find the highest power of x to determine the degree.
  2. Identify the term containing the highest power of x to find the leading term.
  3. Identify the coefficient of the leading term.

Example 8B.1.A

For the following polynomials, identify the degree, the leading term, and the leading coefficient.
  1. [latex]3+2{x}^{2}-4{x}^{3}[/latex]
  2. [latex]5{t}^{5}-2{t}^{3}+7t[/latex]
  3. [latex]6p-{p}^{3}-2[/latex]

Answer:

  1. The highest power of x is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-4{x}^{3}[/latex]. The leading coefficient is the coefficient of that term, [latex]-4[/latex].
  2. The highest power of t is [latex]5[/latex], so the degree is [latex]5[/latex]. The leading term is the term containing that degree, [latex]5{t}^{5}[/latex]. The leading coefficient is the coefficient of that term, [latex]5[/latex].
  3. The highest power of p is [latex]3[/latex], so the degree is [latex]3[/latex]. The leading term is the term containing that degree, [latex]-{p}^{3}[/latex], The leading coefficient is the coefficient of that term, [latex]-1[/latex].

  In the following video example, we will identify the terms, leading coefficient, and degree of a polynomial. https://youtu.be/3u16B2PN9zk The table below illustrates some examples of monomials, binomials, trinomials, and other polynomials. They are all written in standard form.
Monomials Binomials Trinomials Other Polynomials
15 [latex]3y+13[/latex] [latex]x^{3}-x^{2}+1[/latex] [latex]5x^{4}+3x^{3}-6x^{2}+2x[/latex]
[latex] \displaystyle \frac{1}{2}x[/latex] [latex]4p-7[/latex] [latex]3x^{2}+2x-9[/latex] [latex]\frac{1}{3}x^{5}-2x^{4}+\frac{2}{9}x^{3}-x^{2}+4x-\frac{5}{6}[/latex]
[latex]-4y^{3}[/latex] [latex]3x^{2}+\frac{5}{8}x[/latex] [latex]3y^{3}+y^{2}-2[/latex] [latex]3t^{3}-3t^{2}-3t-3[/latex]
[latex]16n^{4}[/latex] [latex]14y^{3}+3y[/latex] [latex]a^{7}+2a^{5}-3a^{3}[/latex] [latex]q^{7}+2q^{5}-3q^{3}+q[/latex]
When the coefficient of a polynomial term is 0, you usually do not write the term at all (because 0 times anything is 0, and adding 0 doesn’t change the value). The last binomial above could be written as a trinomial, [latex]14y^{3}+0y^{2}+3y[/latex]. A term without a variable is called a constant term, and the degree of that term is 0. For example 13 is the constant term in [latex]3y+13[/latex]. You would usually say that [latex]14y^{3}+3y[/latex] has no constant term or that the constant term is 0.

8B.1.1 Evaluate a polynomial

You can evaluate polynomials just as you have been evaluating expressions all along. To evaluate an expression for a value of the variable, you substitute the value for the variable every time it appears. Then use the order of operations to find the resulting value for the expression.

Example 8B.1.B

Evaluate [latex]3x^{2}-2x+1[/latex] for [latex]x=-1[/latex].

Answer: Substitute [latex]-1[/latex] for each x in the polynomial.

[latex]3\left(-1\right)^{2}-2\left(-1\right)+1[/latex]

Following the order of operations, evaluate exponents first.

[latex]3\left(1\right)-2\left(-1\right)+1[/latex]

Multiply 3 times 1, and then multiply [latex]-2[/latex] times [latex]-1[/latex].

[latex]3+\left(-2\right)\left(-1\right)+1[/latex]

Change the subtraction to addition of the opposite.

[latex]3+2+1[/latex]

Find the sum.

Answer

[latex-display]3x^{2}-2x+1=6[/latex], for [latex]x=-1[/latex-display]

Example 8B.1.C

Evaluate [latex] \displaystyle -\frac{2}{3}p^{4}+2p^{3}-p[/latex] for [latex]p = 3[/latex].

Answer: Substitute 3 for each p in the polynomial.

[latex] \displaystyle -\frac{2}{3}\left(3\right)^{4}+2\left(3\right)^{3}-3[/latex]

Following the order of operations, evaluate exponents first and then multiply.

[latex] \displaystyle -\frac{2}{3}\left(81\right)+2\left(27\right)-3[/latex]

Add and then subtract to get [latex]-3[/latex].

[latex]-54 + 54 – 3[/latex]

Answer

[latex-display] \displaystyle -\frac{2}{3}p^{4}+2p^{3}-p=-3[/latex], for [latex]p = 3[/latex-display]

 IN the following video we show more examples of evaluating polynomials for given values of the variable.

https://youtu.be/2EeFrgQP1hM

8B.1.2 Add and Subtract Polynomials

We can add and subtract polynomials by combining like terms, which are terms that contain the same variables raised to the same exponents. For example, [latex]5{x}^{2}[/latex] and [latex]-2{x}^{2}[/latex] are like terms, and can be added to get [latex]3{x}^{2}[/latex], but [latex]3x[/latex] and [latex]3{x}^{2}[/latex] are not like terms, and therefore cannot be added.

Example 8B.1.D

Find the sum.

[latex]\left(12{x}^{2}+9x - 21\right)+\left(4{x}^{3}+8{x}^{2}-5x+20\right)[/latex]

Answer:

[latex]\begin{array}{cc}4{x}^{3}+\left(12{x}^{2}+8{x}^{2}\right)+\left(9x - 5x\right)+\left(-21+20\right) \hfill & \text{Combine like terms}.\hfill \\ 4{x}^{3}+20{x}^{2}+4x - 1\hfill & \text{Simplify}.\hfill \end{array}[/latex]

Here is a summary of some helpful steps for adding and subtracting polynomials.

 Given multiple polynomials, add or subtract them to simplify the expressions.

  1. Combine like terms.
  2. Simplify and write in standard form.
When you subtract polynomials you will still be looking for like terms to combine, but you will need to pay attention to the sign of the terms you are combining. In the following example we will show how to distribute the negative sign to each term of a polynomial that is being subtracted from another.

Example 8B.1.E

Find the difference.

[latex]\left(7{x}^{4}-{x}^{2}+6x+1\right)-\left(5{x}^{3}-2{x}^{2}+3x+2\right)[/latex]

Answer:

[latex]\begin{array}{cc}7{x}^{4}-5{x}^{3}+\left(-{x}^{2}+2{x}^{2}\right)+\left(6x - 3x\right)+\left(1 - 2\right)\text{ }\hfill & \text{Combine like terms}.\hfill \\ 7{x}^{4}-5{x}^{3}+{x}^{2}+3x - 1\hfill & \text{Simplify}.\hfill \end{array}[/latex]

Analysis of the Solution

Note that finding the difference between two polynomials is the same as adding the opposite of the second polynomial to the first. In the following video we show more examples of adding and subtracting polynomials. https://youtu.be/jiq3toC7wGM

8B.1.3 Multiplying Polynomials

Multiplying polynomials is a bit more challenging than adding and subtracting polynomials. We must use the distributive property to multiply each term in the first polynomial by each term in the second polynomial. We then combine like terms. You may have used the distributive property to help you solve linear equations such as [latex]2\left(x+7\right)=21[/latex]. We can distribute the [latex]2[/latex] in [latex]2\left(x+7\right)[/latex] to obtain the equivalent expression [latex]2x+14[/latex]. When multiplying polynomials, the distributive property allows us to multiply each term of the first polynomial by each term of the second. We then add the products together and combine like terms to simplify. The following video will provide you with examples of using the distributive property to find the product of monomials and polynomials. https://youtu.be/bwTmApTV_8o Below is a summary of the steps we used to find the product of two polynomials using the distributive property.

How To: Given the multiplication of two polynomials, use the distributive property to simplify the expression.

  1. Multiply each term of the first polynomial by each term of the second.
  2. Combine like terms.
  3. Simplify.

8B.1.4 Using FOIL to Multiply Binomials

We can also use a shortcut called the FOIL method when multiplying binomials. It is called FOIL because we multiply the first terms, the outer terms, the inner terms, and then the last terms of each binomial. Two quantities in parentheses are being multiplied, the first being: a times x plus b and the second being: c times x plus d. This expression equals ac times x squared plus ad times x plus bc times x plus bd. The terms ax and cx are labeled: First Terms. The terms ax and d are labeled: Outer Terms. The terms b and cx are labeled: Inner Terms. The terms b and d are labeled: Last Terms. The FOIL method arises out of the distributive property. We are simply multiplying each term of the first binomial by each term of the second binomial, and then combining like terms.

Example 8B.1.F

Use FOIL to find the product. [latex](2x-18)(3x+3)[/latex]

Answer: Find the product of the first terms. Find the product of the outer terms. Find the product of the inner terms. Find the product of the last terms.

[latex]\begin{array}{cc}6{x}^{2}+6x - 54x - 54\hfill & \text{Add the products}.\hfill \\ 6{x}^{2}+\left(6x - 54x\right)-54\hfill & \text{Combine like terms}.\hfill \\ 6{x}^{2}-48x - 54\hfill & \text{Simplify}.\hfill \end{array}[/latex]

In this video, we show an example of how to use the FOIL method to multiply two binomials. https://youtu.be/_MrdEFnXNGA The following steps summarize the process for using FOIL to multiply two binomials.  It is very important to note that this process only works for the product of two binomials. If you are multiplying a binomial and a trinomial, it is better to use a table to keep track of your terms.

How To: Given two binomials, use FOIL to simplify the expression.

  1. Multiply the first terms of each binomial.
  2. Multiply the outer terms of the binomials.
  3. Multiply the inner terms of the binomials.
  4. Multiply the last terms of each binomial.
  5. Add the products.
  6. Combine like terms and simplify.

8B.1.5 Multiply a Trinomial and a Binomial

Another type of polynomial multiplication problem is the product of a binomial and trinomial. Although the FOIL method can not be used since there are more than two terms in a trinomial, you still use the Distributive Property to organize the individual products. Using the distributive property, each term in the binomial must be multiplied by each of the terms in the trinomial. For our first examples, we will show you two ways to organize all of the terms that result from multiplying polynomials with more than two terms. The most important part of the process is finding a way to organize terms.

Example 8B.1.G

Find the product.  [latex]\left(3x+6\right)\left(5x^{2}+3x+10\right)[/latex].

Answer: Distribute the trinomial to each term in the binomial. [latex-display]3x\left(5x^{2}+3x+10\right)+6\left(5x^{2}+3x+10\right)[/latex-display] Use the distributive property to distribute the monomials to each term in the trinomials. [latex-display]3x\left(5x^{2}\right)+3x\left(3x\right)+3x\left(10\right)+6\left(5x^{2}\right)+6\left(3x\right)+6\left(10\right)[/latex-display] Multiply. [latex-display]15x^{3}+9x^{2}+30x+30x^{2}+18x+60[/latex-display] Group like terms. [latex-display]15x^{3}+\left(9x^{2}+30x^{2}\right)+\left(30x+18x\right)+60[/latex-display] Combine like terms.

Answer

[latex-display]\left(3x+6\right)\left(5x^{2}+3x+10\right)=15x^{3}+39x^{2}+48x+60[/latex-display]

As you can see, multiplying a binomial by a trinomial leads to a lot of individual terms! Using the same problem as above, we will show another way to organize all the terms produced by multiplying two polynomials with more than two terms.

Example 8B.1.H

Multiply. [latex]\left(3x+6\right)\left(5x^{2}+3x+10\right)[/latex]

Answer: Set up the problem in a vertical form, and begin by multiplying [latex]3x+6[/latex] by [latex]+10[/latex]. Place the products underneath, as shown. [latex-display]\begin{array}{r}3x+\,\,\,6\,\\\underline{\times\,\,\,\,\,\,5x^{2}+\,\,3x+10}\\+30x+60\,\end{array}[/latex-display] Now multiply [latex]3x+6[/latex] by [latex]+3x[/latex]. Notice that [latex]\left(6\right)\left(3x\right)=18x[/latex]; since this term is like [latex]30x[/latex], place it directly beneath it. [latex-display]\begin{array}{r}3x\,\,\,\,\,\,+\,\,\,6\,\,\\\underline{\times\,\,\,\,\,\,5x^{2}\,\,\,\,\,\,+3x\,\,\,\,\,\,+10}\\+30x\,\,\,\,\,+60\,\,\\+9x^{2}\,\,\,+18x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex-display] Finally, multiply [latex]3x+6[/latex] by [latex]5x^{2}[/latex]. Notice that [latex]30x^{2}[/latex] is placed underneath [latex]9x^{2}[/latex]. [latex-display]\begin{array}{r}3x\,\,\,\,\,\,+\,\,\,6\,\,\\\underline{\times\,\,\,\,\,\,5x^{2}\,\,\,\,\,\,+3x\,\,\,\,\,\,+10}\\+30x\,\,\,\,\,+60\,\,\\+9x^{2}\,\,\,+18x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\underline{+15x^{3}+30x^{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}[/latex-display] Now add like terms. [latex-display]\begin{array}{r}3x\,\,\,\,\,\,+\,\,\,6\,\,\\\underline{\times\,\,\,\,\,\,5x^{2}\,\,\,\,\,\,+3x\,\,\,\,\,\,+10}\\+30x\,\,\,\,\,+60\,\,\\+9x^{2}\,\,\,+18x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\underline{+15x^{3}\,\,\,\,\,\,+30x^{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\+15x^{3}\,\,\,\,\,\,+39x^{2}\,\,\,\,+48x\,\,\,\,\,+60\end{array}[/latex-display]

Answer

[latex-display]15x^{3}+39x^{2}+48x+60[/latex-display]

Notice that although the two problems were solved using different strategies, the product is the same. Both the horizontal and vertical methods apply the Distributive Property to multiply a binomial by a trinomial. In our next example we will multiply a binomial and a trinomial that contains subtraction. Pay attention to the signs on the terms.  Forgetting a negative sign is the easiest mistake to make in this case.

Example 8B.1.I

Find the product. [latex-display]\left(2x+1\right)\left(3{x}^{2}-x+4\right)[/latex-display]

Answer: [latex-display]\begin{array}{cc}2x\left(3{x}^{2}-x+4\right)+1\left(3{x}^{2}-x+4\right) \hfill & \text{Use the distributive property}.\hfill \\ \left(6{x}^{3}-2{x}^{2}+8x\right)+\left(3{x}^{2}-x+4\right)\hfill & \text{Multiply}.\hfill \\ 6{x}^{3}+\left(-2{x}^{2}+3{x}^{2}\right)+\left(8x-x\right)+4\hfill & \text{Combine like terms}.\hfill \\ 6{x}^{3}+{x}^{2}+7x+4 \hfill & \text{Simplify}.\hfill \end{array}[/latex-display]

Analysis of the Solution

Another way to keep track of all the terms involved in this product is to use a table, as shown below. Write one polynomial across the top and the other down the side. For each box in the table, multiply the term for that row by the term for that column. Then add all of the terms together, combine like terms, and simplify. Notice how we kept the sign on each term, for example we are subtracting [latex]x[/latex] from [latex]3x^2[/latex], so we place [latex]-x[/latex] in the table.
[latex]3{x}^{2}[/latex] [latex]-x[/latex] [latex]+4[/latex]
[latex]2x[/latex] [latex]6{x}^{3}\\[/latex] [latex]-2{x}^{2}[/latex] [latex]8x[/latex]
[latex]+1[/latex] [latex]3{x}^{2}[/latex] [latex]-x[/latex] [latex]4[/latex]

Example 8B.1.J

Multiply.  [latex]\left(2p-1\right)\left(3p^{2}-3p+1\right)[/latex]

Answer: Distribute 2p and -1 to each term in the trinomial.

[latex]2p\left(3p^{2}-3p+1\right)-1\left(3p^{2}-3p+1\right)[/latex]

[latex]2p\left(3p^{2}\right)+2p\left(-3p\right)+2p\left(1\right)-1\left(3p^{2}\right)-1\left(-3p\right)-1\left(1\right)[/latex]

Multiply. (Notice that the subtracted 1 and the subtracted 3p have a positive product that is added.)

[latex]6p^{3}-6p^{2}+2p-3p^{2}+3p-1[/latex]

Combine like terms.

[latex]6p^{3}-9p^{2}+5p-1[/latex]

Answer

[latex-display]6p^{3}-9p^{2}+5p-1[/latex-display]

In the following video we show more examples of multiplying polynomials. https://youtu.be/bBKbldmlbqI

8B.1.6 Divide a polynomial by a binomial

Dividing a polynomial by a monomial can be handled by dividing each term in the polynomial separately. This can’t be done when the divisor has more than one term. However, the process of long division can be very helpful with polynomials. Recall how you can use long division to divide two whole numbers, say 900 divided by 37.

[latex]37\overline{)900}[/latex]

The dividend in 900 and the divisor is 37. First, you would think about how many 37s are in 90, as 9 is too small. (Note: you could also think, how many 40s are there in 90.)

[latex]\begin{array}\,\,\,\,\,\,\,\,\,\,\,\,2\\37\overline{)900}\\\,\,\,\,\,\,\,\,74\end{array}[/latex]

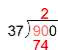Screen Shot 2016-03-28 at 3.35.17 PM There are two 37s in 90, so write 2 above the last digit of 90. Two 37s is 74; write that product below the 90.

[latex]\begin{array}\,\,\,\,\,\,\,\,\,\,\,\,2\\37\overline{)900}\\\,\,\,\,\,\underline{-74}\\\,\,\,\,\,\,\,16\end{array}[/latex]

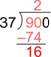Subtract: [latex]90–74[/latex] is 16. (If the result is larger than the divisor, 37, then you need to use a larger number for the quotient.)

[latex]\begin{array}\,\,\,\,\,\,\,\,\,\,\,\,2\\37\overline{)900}\\\,\,\,\,\,\underline{-74}\\\,\,\,\,\,\,\,160\end{array}[/latex]

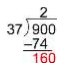Screen Shot 2016-03-28 at 3.36.06 PM Bring down the next digit (0) and consider how many 37s are in 160.

[latex]\begin{array}\,\,\,\,\,\,\,\,\,\,\,\,2\\37\overline{)900}\\\,\,\,\,\,\underline{-74}\\\,\,\,\,\,\,\,160\\\,\,\,\underline{-148}\end{array}[/latex]

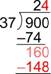There are four 37s in 160, so write the 4 next to the two in the quotient. Four 37s is 148; write that product below the 160. 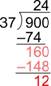Subtract: [latex]160–148[/latex] is 12. This is less than 37 so the 4 is correct. Since there are no more digits in the dividend to bring down, you’re done. The final answer is 24 R12, or [latex]24\frac{12}{37}[/latex]. You can check this by multiplying the quotient (without the remainder) by the divisor, and then adding in the remainder. The result should be the dividend:

[latex]24\cdot37+12=888+12=900[/latex]

To divide polynomials, use the same process. This example shows how to do this when dividing by a binomial.

Example 8B.1.K

Divide: [latex]\frac{\left(x^{2}–4x–12\right)}{\left(x+2\right)}[/latex]

Answer: How many x’s are there in [latex]x^{2}[/latex]? That is, what is [latex] \frac{{{x}^{2}}}{x}[/latex]? [latex] \frac{{{x}^{2}}}{x}=x[/latex]. Put x in the quotient above the [latex]-4x[/latex] term. (These are like terms, which helps to organize the problem.) Write the product of the divisor and the part of the quotient you just found under the dividend. Since [latex]x\left(x+2\right)=x^{2}+2x[/latex], write this underneath, and get ready to subtract. Rewrite [latex]–\left(x^{2} + 2x\right)[/latex] as its opposite [latex]–x^{2}–2x[/latex] so that you can add the opposite. (Adding the opposite is the same as subtracting, and it is easier to do.) Add [latex]-x^{2}[/latex] to [latex]x^{2}[/latex], and [latex]-2x[/latex] to [latex]-4x[/latex]. Bring down [latex]-12[/latex]. Screen Shot 2016-03-28 at 4.19.50 PM Repeat the process. How many times does x go into [latex]-6x[/latex]? In other words, what is [latex] \frac{-6x}{x}[/latex]? Since [latex] \frac{-6x}{x}=-6[/latex], write [latex]-6[/latex] in the quotient. Multiply [latex]-6[/latex] and [latex]x+2[/latex] and prepare to subtract the product. Screen Shot 2016-03-28 at 4.24.52 PM Rewrite [latex]–\left(-6x–12\right)[/latex] as [latex]6x+12[/latex], so that you can add the opposite. Add. In this case, there is no remainder, so you’re done.

Answer

[latex-display]\frac{\left(x^{2}–4x–12\right)}{\left(x+2\right)}=x–6[/latex-display]

Check this by multiplying:

[latex]\left(x-6\right)\left(x+2\right)=x^{2}+2x-6x-12=x^{2}-4x-12[/latex]

In this video we show another example of dividing a degree two trinomial by a degree one binomial. https://youtu.be/KUPFg__Djzw Let’s try another example. In this example, a term is “missing” from the dividend.

Example 8B.1.L

Divide: [latex]\frac{\left(x^{3}–6x–10\right)}{\left(x–3\right)}[/latex]

Answer: In setting up this problem, notice that there is an [latex]x^{3}[/latex] term but no [latex]x^{2}[/latex] term. Add [latex]0x^{2}[/latex] as a “place holder” for this term. (Since 0 times anything is 0, you’re not changing the value of the dividend.) Focus on the first terms again: how many x’s are there in [latex]x^{3}[/latex]? Since [latex] \frac{{{x}^{3}}}{x}=x^{2}[/latex], put [latex]x^{2}[/latex] in the quotient. Multiply [latex]x^{2}\left(x–3\right)=x^{3}–3x^{2}[/latex], write this underneath the dividend, and prepare to subtract. Rewrite the subtraction using the opposite of the expression [latex]x^{3}-3x^{2}[/latex]. Then add. Bring down the rest of the expression in the dividend. It’s helpful to bring down all of the remaining terms. Now, repeat the process with the remaining expression, [latex]3x^{2}-6x–10[/latex], as the dividend. Remember to watch the signs! How many x’s are there in 3x? Since there are 3, multiply [latex]3\left(x–3\right)=3x–9[/latex], write this underneath the dividend, and prepare to subtract. Continue until the degree of the remainder is less than the degree of the divisor. In this case the degree of the remainder, [latex]-1[/latex], is 0, which is less than the degree of [latex]x-3[/latex], which is 1. Also notice that you have brought down all the terms in the dividend, and that the quotient extends to the right edge of the dividend. These are other ways to check whether you have completed the problem. You can write the remainder using the symbol R, or as a fraction added to the rest of the quotient with the remainder in the numerator and the divisor in the denominator. In this case, since the remainder is negative, you can also subtract the opposite.

Answer

[latex-display]\begin{array}{r}{\left(x^{3}–6x–10\right)}{\left(x–3\right)}=x^{2}+3x+3+R-1,\\x^{2}+3x+3+\frac{-1}{x-3}, \text{ or }\\x^{2}+3x+3-\frac{1}{x-3}\end{array}[/latex-display]

Check the result:

[latex]\left(x–3\right)\left(x^{2}+3x+3\right)\,\,\,=\,\,\,x\left(x^{2}+3x+3\right)–3\left(x^{2}+3x+3\right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\,\,\,x^{3}+3x^{2}+3x–3x^{2}–9x–9\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\,\,\,x^{3}–6x–9\\\,\,\,\,\,\,\,\,x^{3}–6x–9+\left(-1\right)\,\,\,=\,\,\,x^{3}–6x–10[/latex]

In the video that follows, we show another example of dividing a degree three trinomial by a binomial, not the "missing" term and how we work with it. https://youtu.be/Rxds7Q_UTeo The process above works for dividing any polynomials, no matter how many terms are in the divisor or the dividend. The main things to remember are:
  • When subtracting, be sure to subtract the whole expression, not just the first term. This is very easy to forget, so be careful!
  • Stop when the degree of the remainder is less than the degree of the dividend, or when you have brought down all the terms in the dividend, and that the quotient extends to the right edge of the dividend.
In this video we present one more example of polynomial long division. https://youtu.be/P6OTbUf8f60

8B.1.7 Synthetic Division

As we’ve seen, long division of polynomials can involve many steps and be quite cumbersome. Synthetic division is a shorthand method of dividing polynomials for the special case of dividing by a polynomial whose leading coefficient is 1.

 Synthetic Division

Synthetic division is a shortcut that can be used when the divisor is a binomial in the form x – k, for a real number k. In synthetic division, only the coefficients are used in the division process.

To illustrate the process, divide [latex]2{x}^{3}-3{x}^{2}+4x+5[/latex] by [latex]x+2[/latex] using the long division algorithm.

.

There is a lot of repetition in this process. If we don’t write the variables but, instead, line up their coefficients in columns under the division sign, we already have a simpler version of the entire problem.

Synthetic division of the polynomial 2x^3-3x^2+4x+5 by x+2 in which it only contains the coefficients of each polynomial.

Synthetic division carries this simplification even a few more steps. Collapse the table by moving each of the rows up to fill any vacant spots. Also, instead of dividing by 2, as we would in division of whole numbers, then multiplying and subtracting the middle product, we change the sign of the "divisor" to –2, multiply and add. The process starts by bringing down the leading coefficient. Synthetic division of the polynomial 2x^3-3x^2+4x+5 by x+2 in which it only contains the coefficients of each polynomial.

We then multiply it by the "divisor" and add, repeating this process column by column, until there are no entries left. The bottom row represents the coefficients of the quotient; the last entry of the bottom row is the remainder. In this case, the quotient is [latex]2x{^2} -7x+18[/latex] and the remainder is –31. The process will be made more clear in the following example.

Example 8B.1.M

Use synthetic division to divide [latex]5{x}^{2}-3x - 36[/latex] by [latex]x - 3[/latex].

Answer:

Begin by setting up the synthetic division. Write 3 and the coefficients of the polynomial.

A collapsed version of the previous synthetic division.

Bring down the lead coefficient. Multiply the lead coefficient by 3 and place the result in the second column.

The set-up of the synthetic division for the polynomial 5x^2-3x-36 by x-3, which renders {5, -3, -36} by 3.

Continue by adding [latex]-3+15[/latex] in the second column. Multiply the resulting number, [latex]12[/latex] by 3. Write the result, [latex]36[/latex] in the next column. Then add the numbers in the third column.

Multiplied by the lead coefficient, 5, in the second column, and the lead coefficient is brought down to the second row.

The result is [latex]5x+12[/latex].

We can check our work by multiplying the result by the original divisor [latex]x-3[/latex], if we get [latex]5{x}^{2}-3x - 36[/latex], we have used the method correctly. Check: [latex](5x+12)(x-3)[/latex]

 [latex]\begin{array}{cc}(5x+12)(x-3)\\=5x^2-15x+12x-36\\=5x^2-3x-36\end{array}[/latex]

Because we got a result of [latex]5{x}^{2}-3x - 36[/latex] when we multiplied the divisor and our answer, we can be sure that we have used synthetic division correctly.

Answer

[latex-display]5{x}^{2}-3x - 36\div{x-3}=5x+12[/latex-display]

Analysis of the solution It is important to note that the result, [latex]5x+12[/latex], of [latex]5{x}^{2}-3x - 36\div{x-3}[/latex] is one degree less than[latex]5{x}^{2}-3x - 36[/latex]. Why is that? Think about how you would have solved this using long division. The first thing you would ask yourself is how many x's are in [latex]5x^2[/latex]?

[latex]x-3\overline{)5{x}^{2}-3x - 36}[/latex]

To get a result of [latex]5x^2[/latex], you need to multiply [latex]x[/latex] by [latex]5x[/latex].  The next step in long division is to subtract this result from [latex]5x^2[/latex].  This leaves us with no [latex]x^2[/latex] term in the result.

Think About It

Reflect on this idea - if you multiply two polynomials and get a result whose degree is 2, what are the possible degrees of the two polynomials that were multiplied? Write your ideas in the box below before looking at the discussion.[practice-area rows="1"][/practice-area]

Answer: A degree two polynomial will have a leading term with [latex]x^2[/latex].  Let's use [latex]2x^2-2x-24[/latex] as an example. We can write two products that will give this as a result of multiplication: [latex-display]2(x^2-x-12) =2x^2-2x-24[/latex-display] [latex-display](2x+6)(x-4)=2x^2-2x-24[/latex-display] If we work backward, starting from [latex]2x^2-2x-24[/latex] if we divide by a binomial with degree one, such as [latex](x-4)[/latex], our result will also have degree one.

In this video example, you will see another example of using synthetic division for division of a degree two polynomial by a degree one binomial. https://youtu.be/KeZ_zMOYu9o

How To: Given two polynomials, use synthetic division to divide.

  1. Write k for the divisor.
  2. Write the coefficients of the dividend.
  3. Bring the lead coefficient down.
  4. Multiply the lead coefficient by k. Write the product in the next column.
  5. Add the terms of the second column.
  6. Multiply the result by k. Write the product in the next column.
  7. Repeat steps 5 and 6 for the remaining columns.
  8. Use the bottom numbers to write the quotient. The number in the last column is the remainder and has degree 0, the next number from the right has degree 1, the next number from the right has degree 2, and so on.
In the next example we will use synthetic division to divide a third-degree polynomial.

Example 8B.1.N

Use synthetic division to divide [latex]4{x}^{3}+10{x}^{2}-6x - 20[/latex] by [latex]x+2[/latex].

Answer: The binomial divisor is [latex]x+2[/latex] so [latex]k=-2[/latex]. Add each column, multiply the result by –2, and repeat until the last column is reached. Synthetic division of 4x^3+10x^2-6x-20 divided by x+2.

The result is [latex]4{x}^{2}+2x - 10[/latex]. Again notice the degree of the result is less than the degree of the quotient, [latex]4{x}^{3}+10{x}^{2}-6x - 20[/latex].

We can check that we are correct by multiplying the result with the divisor: [latex-display](x+2)(4{x}^{2}+2x - 10)=4x^3+2x^2-10x+8x^2+4x-20=4x^3+10x^2-6x-20[/latex-display]

Answer

[latex-display]4{x}^{3}+10{x}^{2}-6x - 20\div{x+2}=4{x}^{2}+2x - 10[/latex-display]

In the next example we will show division of a fourth degree polynomial by a binomial.  Note how there is no x term in the fourth degree polynomial, so we need to use a placeholder of 0 to ensure proper alignment of terms.

Example 8B.1.O

Use synthetic division to divide [latex]-9{x}^{4}+10{x}^{3}+7{x}^{2}-6[/latex] by [latex]x - 1[/latex].

Answer:

Notice there is no x-term. We will use a zero as the coefficient for that term. .

The result is [latex]-9{x}^{3}+{x}^{2}+8x+8+\frac{2}{x - 1}[/latex].

In our last video example we show another example of how to use synthetic division to divide a degree three polynomial by a degree one binomial. https://youtu.be/h1oSCNuA9i0

Summary

Multiplication of binomials and polynomials requires use of the distributive property as well as the commutative and associative properties of multiplication. Whether the polynomials are monomials, binomials, or trinomials, carefully multiply each term in one polynomial by each term in the other polynomial. Be careful to watch the addition and subtraction signs and negative coefficients. A product is written in simplified form if all of its like terms have been combined. Dividing polynomials by polynomials of more than one term can be done using a process very much like long division of whole numbers. You must be careful to subtract entire expressions, not just the first term. Stop when the degree of the remainder is less than the degree of the divisor. The remainder can be written using R notation, or as a fraction added to the quotient with the remainder in the numerator and the divisor in the denominator.

Licenses & Attributions

CC licensed content, Original

  • Evaluate a Polynomial in One Variable. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
  • Ex: Multiplying Using the Distributive Property. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Multiply Binomials Using An Area Model and Using Repeated Distribution. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Multiply Binomials Using the FOIL Acronym. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Divide a Degree 3 Polynomial by a Degree 1 Polynomial (Long Division with Missing Term). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Screenshot Polynomial Generated Images. Provided by: Lumen Learning License: CC BY: Attribution.

CC licensed content, Shared previously

  • Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
  • College Algebra. Authored by: Abramson, Jay, et al.. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: Public Domain: No Known Copyright. License terms: Download for free at :http://cnx.org/contents/[email protected]:1/Preface.
  • Ex: Intro to Polynomials in One Variable. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex: Adding and Subtracting Polynomials. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Ex: Polynomial Multiplication Involving Binomials and Trinomials. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex 1: Divide a Trinomial by a Binomial Using Long Division. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Ex 6: Divide a Polynomial by a Degree Two Binomial Using Long Division. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex 1: Divide a Trinomial by a Binomial Using Synthetic Division. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex 3: Divide a Polynomial by a Binomial Using Synthetic Division. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.