Characteristics of Linear Functions and Their Graphs
5.1 Learning Objectives
- Slope
- Define slope for a linear function
- Calculate slope given two points
- Graph and Transform
- Graph a linear function using the slope and y-intercept
- Define and use a vertical stretch or compression to graph a linear function
- Define and use a vertical shift to graph a linear function
- Combine transformations to graph a linear function

Imagine placing a plant in the ground one day and finding that it has doubled its height just a few days later. Although it may seem incredible, this can happen with certain types of bamboo species. These members of the grass family are the fastest-growing plants in the world. One species of bamboo has been observed to grow nearly 1.5 inches every hour. In a twenty-four hour period, this bamboo plant grows about 36 inches, or an incredible 3 feet! A constant rate of change, such as the growth cycle of this bamboo species, is a linear function.
One well known form for writing linear functions is known as the slope-intercept form, where [latex]x[/latex] is the input value, [latex]m[/latex] is the rate of change, and [latex]b[/latex] is the initial value of the dependant variable.[latex]\begin{array}{cc}\text{Equation form}\hfill & y=mx+b\hfill \\ \text{Function notation}\hfill & f\left(x\right)=mx+b\hfill \end{array}[/latex]
We often need to calculate the slope given input and output values. Given two values for the input, [latex]{x}_{1}[/latex] and [latex]{x}_{2}[/latex], and two corresponding values for the output, [latex]{y}_{1}[/latex] and [latex]{y}_{2}[/latex] —which can be represented by a set of points, [latex]\left({x}_{1}\text{, }{y}_{1}\right)[/latex] and [latex]\left({x}_{2}\text{, }{y}_{2}\right)[/latex]—we can calculate the slope [latex]m[/latex], as follows[latex]m=\frac{\text{change in output (rise)}}{\text{change in input (run)}}=\frac{\Delta y}{\Delta x}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]
where [latex]\Delta y[/latex] is the vertical displacement and [latex]\Delta x[/latex] is the horizontal displacement. Note in function notation two corresponding values for the output [latex]{y}_{1}[/latex] and [latex]{y}_{2}[/latex] for the function [latex]f[/latex], [latex]{y}_{1}=f\left({x}_{1}\right)[/latex] and [latex]{y}_{2}=f\left({x}_{2}\right)[/latex], so we could equivalently write[latex]m=\frac{f\left({x}_{2}\right)-f\left({x}_{1}\right)}{{x}_{2}-{x}_{1}}[/latex]
The graph in Figure 5 indicates how the slope of the line between the points, [latex]\left({x}_{1,}{y}_{1}\right)[/latex] and [latex]\left({x}_{2,}{y}_{2}\right)[/latex], is calculated. Recall that the slope measures steepness. The greater the absolute value of the slope, the steeper the line is. The slope of a function is calculated by the change in [latex]y[/latex] divided by the change in [latex]x[/latex]. It does not matter which coordinate is used as the [latex]\left({x}_{2,\text{ }}{y}_{2}\right)[/latex] and which is the [latex]\left({x}_{1},\text{ }{y}_{1}\right)[/latex], as long as each calculation is started with the elements from the same coordinate pair.
The units for slope are always [latex]\frac{\text{units for the output}}{\text{units for the input}}[/latex] Think of the units as the change of output value for each unit of change in input value. An example of slope could be miles per hour or dollars per day. Notice the units appear as a ratio of units for the output per units for the input.
The slope of a function is calculated by the change in [latex]y[/latex] divided by the change in [latex]x[/latex]. It does not matter which coordinate is used as the [latex]\left({x}_{2,\text{ }}{y}_{2}\right)[/latex] and which is the [latex]\left({x}_{1},\text{ }{y}_{1}\right)[/latex], as long as each calculation is started with the elements from the same coordinate pair.
The units for slope are always [latex]\frac{\text{units for the output}}{\text{units for the input}}[/latex] Think of the units as the change of output value for each unit of change in input value. An example of slope could be miles per hour or dollars per day. Notice the units appear as a ratio of units for the output per units for the input.
Calculate Slope
The slope, or rate of change, of a function [latex]m[/latex] can be calculated according to the following: [latex-display]m=\frac{\text{change in output (rise)}}{\text{change in input (run)}}=\frac{\Delta y}{\Delta x}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex-display] where [latex]{x}_{1}[/latex] and [latex]{x}_{2}[/latex] are input values, [latex]{y}_{1}[/latex] and [latex]{y}_{2}[/latex] are output values.Example 5.1.A
If [latex]f\left(x\right)[/latex] is a linear function, and [latex]\left(3,-2\right)[/latex] and [latex]\left(8,1\right)[/latex] are points on the line, find the slope. Is this function increasing or decreasing?Answer: The coordinate pairs are [latex]\left(3,-2\right)[/latex] and [latex]\left(8,1\right)[/latex]. To find the rate of change, we divide the change in output by the change in input.
[latex]m=\frac{\text{change in output}}{\text{change in input}}=\frac{1-\left(-2\right)}{8 - 3}=\frac{3}{5}[/latex]
We could also write the slope as [latex]m=0.6[/latex]. The function is increasing because [latex]m>0[/latex]. As noted earlier, the order in which we write the points does not matter when we compute the slope of the line as long as the first output value, or y-coordinate, used corresponds with the first input value, or x-coordinate, used.Example 5.1.B
The population of a city increased from 23,400 to 27,800 between 2008 and 2012. Find the change of population per year if we assume the change was constant from 2008 to 2012.Answer: The rate of change relates the change in population to the change in time. The population increased by [latex]27,800-23,400=4400[/latex] people over the four-year time interval. To find the rate of change, divide the change in the number of people by the number of years.
[latex]\frac{4,400\text{ people}}{4\text{ years}}=1,100\text{ }\frac{\text{people}}{\text{year}}[/latex]
So the population increased by 1,100 people per year. Because we are told that the population increased, we would expect the slope to be positive. This positive slope we calculated is therefore reasonable.Graph Linear Functions Using Slope and y-Intercept
Another way to graph a linear function is by using its slope m, and y-intercept. Let’s consider the following function.[latex]f\left(x\right)=\frac{1}{2}x+1[/latex]
The slope is [latex]\frac{1}{2}[/latex]. Because the slope is positive, we know the graph will slant upward from left to right. The y-intercept is the point on the graph when x = 0. The graph crosses the y-axis at (0, 1). Now we know the slope and the y-intercept. We can begin graphing by plotting the point (0, 1) We know that the slope is rise over run, [latex]m=\frac{\text{rise}}{\text{run}}[/latex]. From our example, we have [latex]m=\frac{1}{2}[/latex], which means that the rise is 1 and the run is 2. So starting from our y-intercept (0, 1), we can rise 1 and then run 2, or run 2 and then rise 1. We repeat until we have a few points, and then we draw a line through the points as shown in the graph below.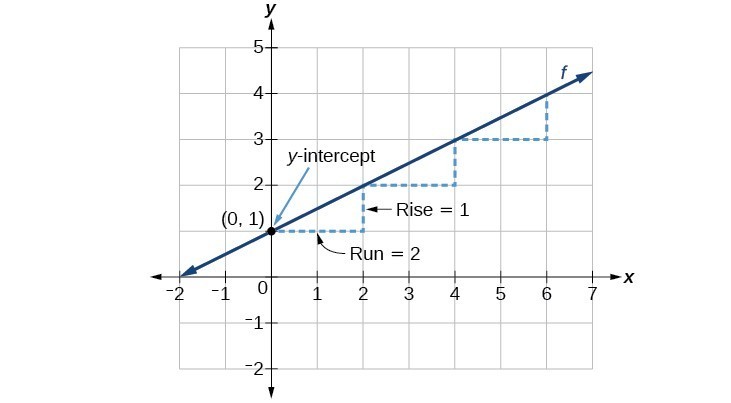
A General Note: Graphical Interpretation of a Linear Function
In the equation [latex]f\left(x\right)=mx+b[/latex]- b is the y-intercept of the graph and indicates the point (0, b) at which the graph crosses the y-axis.
- m is the slope of the line and indicates the vertical displacement (rise) and horizontal displacement (run) between each successive pair of points. Recall the formula for the slope:
[latex]m=\frac{\text{change in output (rise)}}{\text{change in input (run)}}=\frac{\Delta y}{\Delta x}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]
How To: Given the equation for a linear function, graph the function using the y-intercept and slope.
- Evaluate the function at an input value of zero to find the y-intercept.
- Identify the slope as the rate of change of the input value.
- Plot the point represented by the y-intercept.
- Use [latex]\frac{\text{rise}}{\text{run}}[/latex] to determine at least two more points on the line.
- Sketch the line that passes through the points.
Example 5.1.C
Graph [latex]f\left(x\right)=-\frac{2}{3}x+5[/latex] using the y-intercept and slope.Answer:
Evaluate the function at [latex]x=0[/latex] to find the y-intercept. The output value when [latex]x=0[/latex] is 5, so the graph will cross the y-axis at (0, 5).
According to the equation for the function, the slope of the line is [latex]-\frac{2}{3}[/latex]. This tells us that for each vertical decrease in the "rise" of [latex]–2[/latex] units, the "run" increases by 3 units in the horizontal direction. We can now graph the function by first plotting the y-intercept in the graph below. From the initial value (0, 5) we move down 2 units and to the right 3 units. We can extend the line to the left and right by repeating, and then draw a line through the points.
 The graph slants downward from left to right, which means it has a negative slope as expected.
The graph slants downward from left to right, which means it has a negative slope as expected.
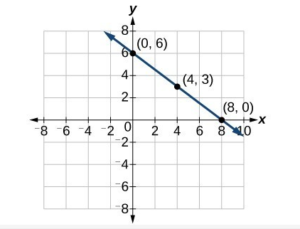
Example 5.1.D
Graph [latex]f\left(x\right)=-\frac{3}{4}x+6[/latex] using the slope and y-intercept.Answer: The slope of this function is [latex]-\frac{3}{4}[/latex] and the y-intercept is [latex](0,6)[/latex] We can start graphing by plotting the y-intercept and counting down three units and right 4 units. The first stop would be [latex](4,3)[/latex], and the next stop would be [latex](0,8)[/latex].
Answer
5.1.1 Graphing a Linear Function Using Transformations
Another option for graphing is to use transformations of the identity function [latex]f\left(x\right)=x[/latex] . A function may be transformed by a shift up, down, left, or right. A function may also be transformed using a reflection, stretch, or compression.Vertical Stretch or Compression
In the equation [latex]f\left(x\right)=mx[/latex], the m is acting as the vertical stretch or compression of the identity function. When m is negative, there is also a vertical reflection of the graph. Notice in the figure below that multiplying the equation of [latex]f\left(x\right)=x[/latex] by m stretches the graph of f by a factor of m units if [latex]m>1[/latex] and compresses the graph of f by a factor of m units if [latex]0<m<1[/latex]. This means the larger the absolute value of m, the steeper the slope.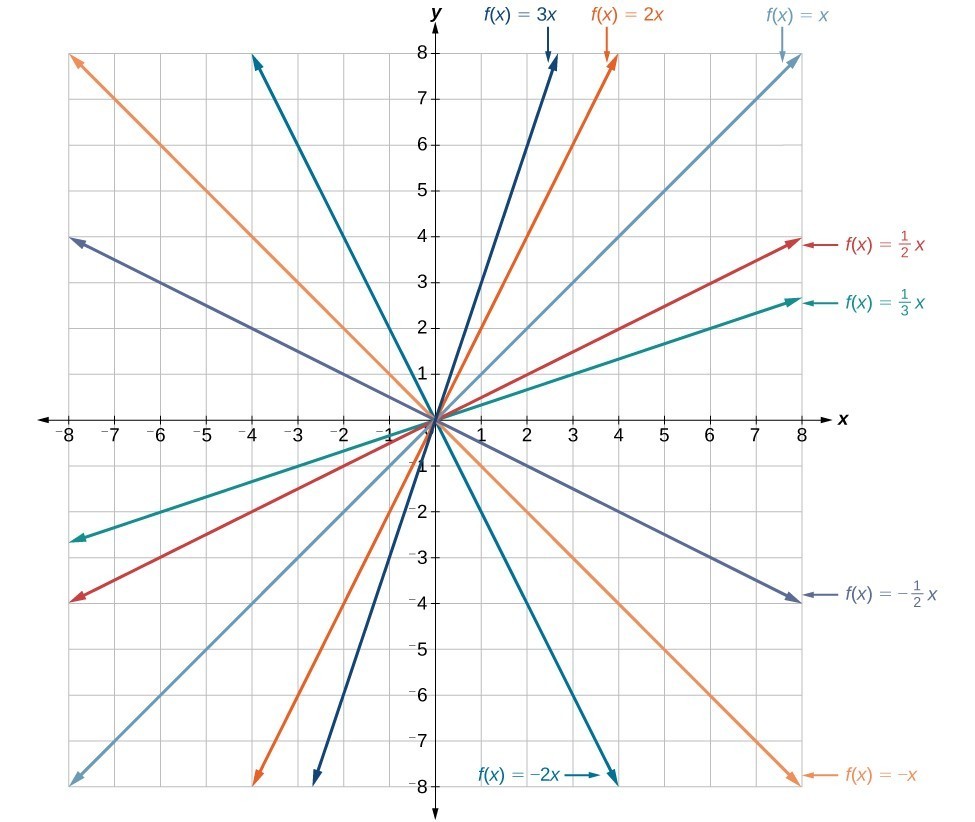 Vertical stretches and compressions and reflections on the function [latex]f\left(x\right)=x[/latex].
Vertical stretches and compressions and reflections on the function [latex]f\left(x\right)=x[/latex].
Vertical Shift
In [latex]f\left(x\right)=mx+b[/latex], the b acts as the vertical shift, moving the graph up and down without affecting the slope of the line. Notice in the figure below that adding a value of b to the equation of [latex]f\left(x\right)=x[/latex] shifts the graph of f a total of b units up if b is positive and [latex]|b|[/latex] units down if b is negative.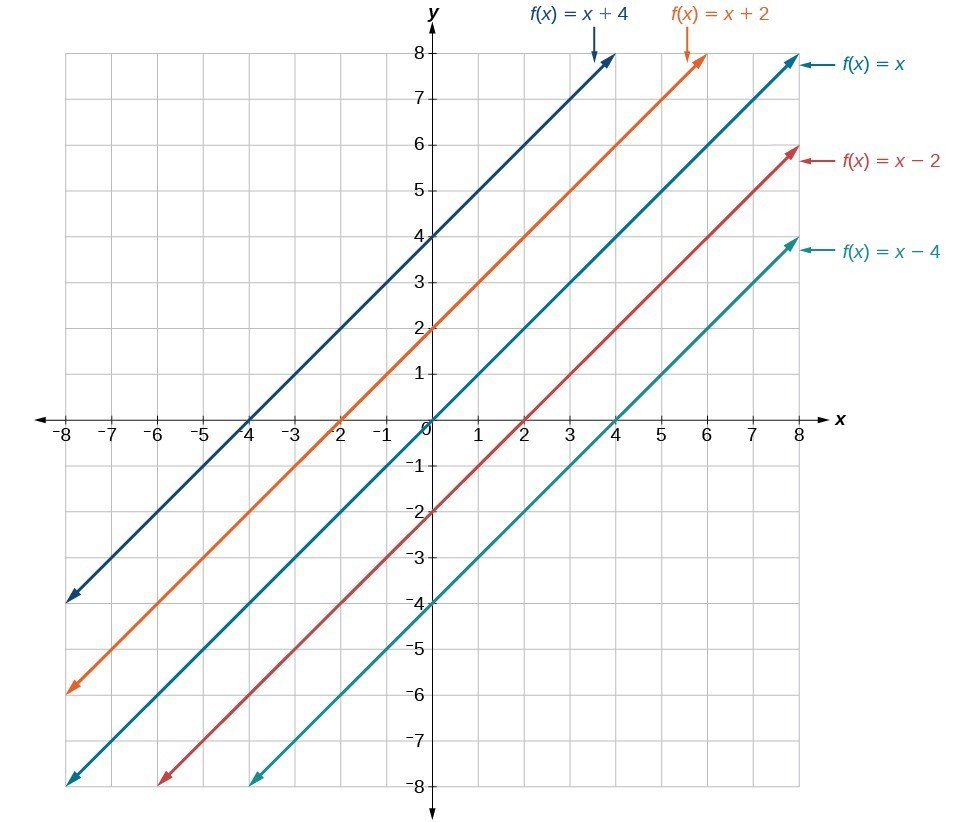 This graph illustrates vertical shifts of the function [latex]f\left(x\right)=x[/latex].
Using vertical stretches or compressions along with vertical shifts is another way to look at identifying different types of linear functions. Although this may not be the easiest way to graph this type of function, it is still important to practice each method.
This graph illustrates vertical shifts of the function [latex]f\left(x\right)=x[/latex].
Using vertical stretches or compressions along with vertical shifts is another way to look at identifying different types of linear functions. Although this may not be the easiest way to graph this type of function, it is still important to practice each method.
How To: Given the equation of a linear function, use transformations to graph the linear function in the form [latex]f\left(x\right)=mx+b[/latex].
- Graph [latex]f\left(x\right)=x[/latex].
- Vertically stretch or compress the graph by a factor |m|.
- Shift the graph up or down b units.
Example 5.1.E
Describe the transformations to the identity for the function [latex]f(x)=\frac{2}{3}x[/latex], and draw a graph.Answer:
In this case, [latex]m=\frac{2}{3}[/latex], so this is a vertical compression since [latex]0<m<1[/latex].
The graph of [latex]f(x)=\frac{2}{3}x[/latex] is plotted below with the identity:
 Note how the identity is compressed because the rate of change is "slowed" by the vertical compression of [latex]\frac{2}{3}[/latex]
Note how the identity is compressed because the rate of change is "slowed" by the vertical compression of [latex]\frac{2}{3}[/latex]
Example 5.1.F
Describe the transformations to the identity for the function [latex]f(x)=2x[/latex], and draw a graph.Answer: In this case, [latex]m=2[/latex], so this is a vertical stretch since [latex]m>1[/latex]. The graph of [latex]f(x)=2x[/latex] is plotted below with the identity:
 y=2x and y=x
y=2x and y=xExample 5.1.G
Describe the transformations to the identity for the function [latex]f(x)=-2x[/latex], and draw a graph.Answer: In this case, [latex]m=-2[/latex], so this is a vertical stretch since [latex]|m|>1[/latex], the negative sign reflects the graph across the y axis. The graph of [latex]f(x)=-2x[/latex] is plotted below with the identity:
 y = x and y = -2x
y = x and y = -2xExample 5.1.H
Graph [latex]f\left(x\right)=\frac{1}{2}x - 3[/latex] using transformations.Answer:
The equation for the function shows that [latex]m=\frac{1}{2}[/latex] so the identity function is vertically compressed by [latex]\frac{1}{2}[/latex]. The equation for the function also shows that [latex]b=–3[/latex] so the identity function is vertically shifted down 3 units. First, graph the identity function, and show the vertical compression.
 The function [latex]y=x[/latex], compressed by a factor of [latex]\frac{1}{2}[/latex].
Then show the vertical shift.
The function [latex]y=x[/latex], compressed by a factor of [latex]\frac{1}{2}[/latex].
Then show the vertical shift.
 The function [latex]y=\frac{1}{2}x[/latex], shifted down 3 units.
The function [latex]y=\frac{1}{2}x[/latex], shifted down 3 units.
Q&A
In the example above, could we have sketched the graph by reversing the order of the transformations? No. The order of the transformations follows the order of operations. When the function is evaluated at a given input, the corresponding output is calculated by following the order of operations. This is why we performed the compression first.Summary
- Vertical compressions of the identity happen when the slope is between 0 and 1
- Vertical stretches of the identity happen when the slope is greater than 1
- Reflections happen when the slope is negative
- Vertical shifts happen when the intercept is not equal to 0
- Transformations can be combined
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Write and Graph a Linear Function by Making a Table of Values (Intro). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Graph a Linear Function as a Transformation of f(x)=x. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution.
- Ex: Find the Slope Given Two Points and Describe the Line. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex: Slope Application Involving Production Costs. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex: Graph a Line and ID the Slope and Intercepts (Fraction Slope). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
